Навигация
Экономико-математическая модель
2.2 Экономико-математическая модель
Целевая функция стремится к максимуму, так как основной целью предприятия является получение максимальной прибыли. В данном случае целевая функция представлена в виде:
14,20х1+14,40х2→max,
где: х1 – количество сыра "Звенигородский" 50%, необходимое производить ОАО "Звенигородский сыркомбинат"; х2 – количество сыра "Российский" 50%, необходимое производить ОАО "Звенигородский сыркомбинат";
В качестве ограничений в данной модели выступают ограничения:
· расходы по оплате труда;
· затраты на производство;
· коммерческие расходы.
Ограничения представлены в виде:
0,51х1+0,55х2≤1175300
9,21х1+9,43х2≤19244000
0,075х1+0,06х2≤143000
х1+х2≤2100000
В результате проведенных вычислений, для того чтобы получать максимальную прибыль в размере 29556793 грн. ОАО "Звенигородский сыркомбинат" необходимо выпускать 1253476 килограмм сыра "Звенигородский" 50% и 816488,8 килограмм сыра "Российский" 50% ежегодно. При соблюдении предложенной программы выпуска продукции сокращаются затраты:
· на расходы по оплате труда – до 1088341 грн;
· затраты на производство – до 19244000 грн;
· коммерческие расходы – до 143000 грн.
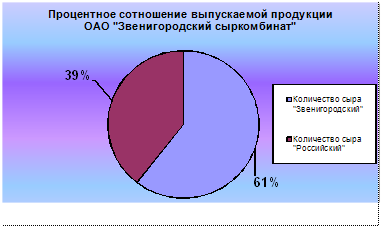
Суммарный выпуск продукции соответственно данной модели составит 2069964 килограмм. Процентное соотношение выпускаемой продукции ОАО " звенигородский сыркомбинакт" представлено на рисунке 1.
2.3 Процентное соотношение выпускаемой продукции
2.4 Оптимальное планирование и математические методы прогнозирования
Во всех отраслях и сферах хозяйственной деятельности приходится постоянно принимать управляющие решения, последствия которых проявятся в будущем. Можно с уверенностью утверждать, что любое такое решение основывается на том или ином способе предвидения.Одним из способов предвидения при принятии хозяйственных решений является прогнозирование.
Прогнозирование – это научная деятельность, направленная на выявление и изучение возможных альтернатив будущего развития и структуры его вероятных траекторий. Каждая альтернативная траектория развития связывается с наличием комплекса внешних относительно исследуемой системы (явления) условий.
Под прогнозированием в экономике понимается научное определение вероятных путей и результатов предстоящего развития экономической системы, оценку показателей, характеризующих это развитие в течении более или менее отдаленного будущего.
Таким образом, цель экономического прогнозирования – предсказание (предвидение) будущих последствий хозяйственных решений, принимаемых в текущий момент времени.
Задачи, решаемые на основе экономических прогнозов, зависят от масштабов и характера деятельности организации. Если это задачи, например, разработки годового регионального или государственного бюджета, то, очевидно, необходимо иметь прогнозы темпов инфляции, объемов поступления налоговых средств и т. д. Если это промышленное предприятие, то такими задачами могут являться определение ассортимента выпускаемой продукции в зависимости от прогнозов на платежеспособный спрос; расширение или свертывание производства в зависимости от прогнозов общеэкономической конъюнктуры и т. п. В любом случае результаты прогнозов всегда лежат в основе планов предстоящей хозяйственной деятельности.
Классифицируют прогнозы по функциональному признаку, т. е. по назначению, и по длительности периода прогнозирования.
По функциональному признаку прогнозы делятся на: стратегические, ориентированные на обеспечение разработки бизнес-планов хозяйственной деятельности и на оперативные, предназначенные для обеспечения разработки текущих планов производственной деятельности фирмы.
По временному признаку различают краткосрочные, среднесрочные и долгосрочные прогнозы. Под краткосрочными прогнозами обычно понимают прогнозы на периоды времени меньшие года. Под среднесрочными – от года до двух-трех лет, под долгосрочными – на более длительные сроки. Однако необходимо помнить, что градация прогнозов по временному фактору существенно зависит от вида деятельности организации, которая занимается прогнозированием. Например, при спекулятивной работе с ценными бумагами долгосрочным прогнозом будет прогноз на несколько дней вперед, а при стратегическом прогнозировании перспективных направлений развития генной инженерии в качестве периода долгосрочного прогноза, очевидно, будет выступать срок порядка десятков лет.
Методы прогнозирования
К числу основных методов прогнозирования относятся:
§ метод Дельфи;
§ регистрационный метод;
§ метод статистического анализа
§ комбинированный метод.
Метод Дельфи основан на обработке субъективных мнений — экспертных оценок специалистов, занятых в интересующей сфере деятельности.
Регистрационный метод основан на анализе постоянно печатающихся в периодике данных деловой активности.
Метод статистического анализа базируется на использовании ретроспективных данных.
Комбинированный метод предполагает совокупное использование всех вышеназванных способов прогнозирования
Методы прогнозирования могут основываться на предположении о предстоящих качественных изменениях системы или сохранении в будущем существующих закономерностей развития. Для долгосрочных прогнозов используются экспертные и логические методы, а для краткосрочных и среднесрочных прогнозов - методы экстраполяции.
Экспертные методы прогнозирования опираются на методы качественного оценивания систем. Но более часто используются разновидности метода Дельфи и метод сценариев в сочетании со статистическими методами.
Логические методы прогнозирования основываются на проведении аналогии функционирования рассматриваемой системы с историей функционирования какой-либо другой системы.
Методы экстраполяции относятся к аналитическим метода прогнозирования состояния систем. Примером экстраполяции служит прогнозирование значений какой-либо величины по имеющимся табличным данным. В качестве исходной информации при этом берутся временные ряды динамики параметров системы - набор наблюдений некоторых числовых характеристик параметров системы, взятых в равноотстоящие или неравноотстоящие моменты времени за определенный период.
В основе методов экстраполяции лежит понятие интерполирования. Известно, что интерполированием называется процесс вычисления промежуточных значений функции на основании заданного ряда значений этой функции. В широком смысле слов; интерполирование - это представление некоторой функции известного или неизвестного вида, ряд значений которой при определенных значениях независимой переменной задан, при помощи другой, более простой функции.
Пусть ![]() будет функцией, заданной рядом значений
будет функцией, заданной рядом значений ![]() которые она принимает при значениях
которые она принимает при значениях ![]() независимой переменной х, и пусть
независимой переменной х, и пусть ![]() обозначает произвольную более простую функцию, принимающую для
обозначает произвольную более простую функцию, принимающую для ![]() те же самые значения, что и
те же самые значения, что и ![]() . Замена
. Замена ![]() в пределах данного интервала на
в пределах данного интервала на ![]() и есть интерполирование.
и есть интерполирование.
Формула ![]() , которая при этом получается для вычисления значений у, называется интерполяционной формулой.
, которая при этом получается для вычисления значений у, называется интерполяционной формулой.
Функция ![]() может иметь различный вид. Когда
может иметь различный вид. Когда ![]() есть полином, процесс замещения
есть полином, процесс замещения ![]() через
через ![]() называется параболическим, или полиномиальным, интерполированием. Когда
называется параболическим, или полиномиальным, интерполированием. Когда ![]() есть тригонометрический полином, процесс называется тригонометрическим интерполированием. Функция
есть тригонометрический полином, процесс называется тригонометрическим интерполированием. Функция ![]() может быть также составлена из показательных функций, полиномов Лежандра, функций Бесселя и т.д. В практических задачах в качестве
может быть также составлена из показательных функций, полиномов Лежандра, функций Бесселя и т.д. В практических задачах в качестве ![]() выбирается простейшая функция, могущая заменить данную функцию на рассматриваемом интервале. Так как самой простой функцией является полином, почти все основные интерполяционные функции являются полиномиальными. В случае, когда известно, что данная функция
выбирается простейшая функция, могущая заменить данную функцию на рассматриваемом интервале. Так как самой простой функцией является полином, почти все основные интерполяционные функции являются полиномиальными. В случае, когда известно, что данная функция ![]() периодична, лучше заменить ее тригонометрическим полиномом.
периодична, лучше заменить ее тригонометрическим полиномом.
Теоретическое обоснование замены данной функции полиномом или тригонометрическим полиномом опирается на две замечательные теоремы, доказанные Вейерштрассом в 1885 г. Эти теоремы можно сформулировать так.
Теорема 1. Любая непрерывная в интервале (а, b) функция может быть заменена в нем с любой степенью точности полиномом. Другими словами, можно найти такой полином Р(х), что ![]() для каждого значения x в интервале (а, b), причем ε есть любая положительная величина.
для каждого значения x в интервале (а, b), причем ε есть любая положительная величина.
Теорема 2. Любая непрерывная с периодом 2π функция может быть заменена тригонометрическим полиномом вида
![]()
так, что ![]() для каждого значения х в рассматриваемом интервале, причем ε есть любая положительная величина. Геометрический смысл этих теорем состоит в том, что если нанести графики функций
для каждого значения х в рассматриваемом интервале, причем ε есть любая положительная величина. Геометрический смысл этих теорем состоит в том, что если нанести графики функций ![]() ,
, ![]() и
и ![]() , то можно найти многочлен или тригонометрический многочлен, график которого будет находиться внутри области, ограниченной кривыми
, то можно найти многочлен или тригонометрический многочлен, график которого будет находиться внутри области, ограниченной кривыми ![]() и
и ![]() при всех значениях х между а и b, как бы мало ни было ε.
при всех значениях х между а и b, как бы мало ни было ε.
При таком представлении процесса интерполирования становится понятно, что экстраполирование - это процесс вычисления значения функции, находящегося за пределами ряда заданных значений.
Экстраполирование нужно применять с осторожностью. Но если известно, что функция около концов данного ряда значений изменяется плавно, и если Δх берется достаточно малым, то можно спокойно экстраполировать на расстояние Δх за пределами ряда имеющихся значений.
Для проведения интерполирования существует ряд формул рассматриваемых в численных методах математического анализа. При их применении в прогнозировании следует учитывать что если число точек ![]() неограниченно возрастает то интерполирующий полином превращается в бесконечный ряд. называемый интерполяционным рядом. И подобно тому как степенной ряд сходится внутри и расходится во вне некоторого определенного интервала, так и интерполяционный ряд сходится к заданной функции внутри некоторого интервала и перестает к ней сходиться вне его.
неограниченно возрастает то интерполирующий полином превращается в бесконечный ряд. называемый интерполяционным рядом. И подобно тому как степенной ряд сходится внутри и расходится во вне некоторого определенного интервала, так и интерполяционный ряд сходится к заданной функции внутри некоторого интервала и перестает к ней сходиться вне его.
Поскольку увеличение периода упреждения прогноза Δх влечет за собой увеличение степени неопределенности процессов развития системы, то в методах экстраполяции выделяют статистические методы.
Прогнозирование, основанное на использовании методов статистического анализа ретроспективных данных, допустимо в том случае, когда между прошлым и будущим имеется определенная причинно-следственная связь. Можно утверждать, что анализ ретроспективных данных служит надежной основой для принятия решений относительно будущих хозяйственных действий, однако не следует забывать, что прогностические оценки, полученные методом статистического анализа, подлежат корректировке в случае, если известны те или иные факторы, влияние которых с той или иной вероятностью ожидается в будущем.
Наиболее характерной задачей прогнозирования, которая решается в каждой фирме, является задача прогнозирования спроса на товары или услуги фирмы. Для решения этой задачи необходимо предварительное изучение рынков сбыта маркетинговыми исследованиями, которые и поставляют необходимую статистическую информацию для применения методов статистического анализа при разработке прогнозов.
Алгоритм построения прогноза методом статистического анализа состоит из следующих шагов:
§ строится график зависимости спроса от времени;
§ на основе визуального изучения графика делается предположение об аналитической форме кривой, которая наилучшим образом способна аппроксимировать ломаную на графике;
§ применяется метод наименьших квадратов для построения прогнозирующей кривой;
§ оценивается среднее значение погрешности полученных прогнозных оценок;
§ принимается решение об использовании или не использовании
§ выбранной кривой для построения прогноза.
Наиболее часто употребляемым методом построения прогнозирующей функции является метод наименьших квадратов.
Метод наименьших квадратов позволяет подобрать некоторую непрерывную аналитическую функцию для аппроксимации дискретного набора исходных данных. Выбор функции считается наилучшим, если сведено к минимуму стандартное отклонение по рассматриваемой временной выборке, которое определяется по формуле:
![]()
где ![]() — фактический спрос, наблюдаемый в t-й период (отрезок) времени;
— фактический спрос, наблюдаемый в t-й период (отрезок) времени;
![]() — значение прогнозирующей функции для того же момента
— значение прогнозирующей функции для того же момента
времени;
п — число периодов (наблюдений), т. е. длина временной выборки;
f – число степеней свободы.
Суммирование ведется по всей выборке, поэтому, как это принято в статистике, нижний и верхний индексы суммирования опущены.
Минимизация ![]() эквивалентна минимизации
эквивалентна минимизации ![]() . Поэтому задача сводится к минимизации суммы квадратов разностей между фактическим значением спроса в момент t и тем значением, которое принимает прогнозирующая функция.
. Поэтому задача сводится к минимизации суммы квадратов разностей между фактическим значением спроса в момент t и тем значением, которое принимает прогнозирующая функция.
Наиболее часто для построения прогнозирующей функции используют линейную функцию ![]() , параболу
, параболу ![]() , гиперболу
, гиперболу ![]() , многочлены более высоких порядков.
, многочлены более высоких порядков.
Статистические методы прогнозирования опираются на теорию вероятностей, математическую статистику и теорию случайных процессов.
К статистическим методам прогнозирования относят:
• методы многофакторного анализа (регрессионные модели,
• адаптивное сглаживание, метод группового учета аргументов,
• имитационные модели, многомерная фильтрация и др.);
• методы однофакторного прогнозирования (экспоненциальное сглаживание, метод скользящего среднего, метод разностных уравнений, спектральные методы, метод марковских цепей, оптимальные фильтры, сплайн-функции, метод авторегрессии и др.).
Прогнозирование на основе тренда и колеблемости
Прогнозирование возможных значений признаков изучаемого объекта — одна из основных задач науки. В ее решении роль статистических методов очень значительна. Одним из них является расчет прогнозов на основе тренда и колеблемости динамического ряда до настоящего времени. Если мы будем знать, как быстро и в каком направлении изменились уровни какого-то признака, то сможем узнать, какого значения достигнет уровень спустя известное время. Методика статистического прогноза по тренду и колеблемости основана на их экстраполяции, т.е. на предположении, что параметры тренда и колебаний сохраняются до прогнозируемого периода. Такая экстраполяция справедлива, если система развивается эволюционно в достаточно стабильных условиях. Чем крупнее система, тем выше вероятность сохранения параметров ее изменения, конечно, на срок не слишком большой. Обычно рекомендуют, чтобы срок прогноза не превышал 1/3 длительности базы расчета тренда.
В отличие от прогноза на основе регрессионного уравнения прогноз по тренду учитывает факторы развития только в неявном виде, и это не позволяет "проигрывать" разные варианты прогнозов при разных возможных значениях факторов, влияющих на изучаемый признак. Зато прогноз по тренду охватывает все факторы, в то время как в регрессионную модель невозможно включить в явном виде более 10—20 факторов в самом лучшем случае.
Прежде чем применить методы математического анализа для вычисления параметров уравнения тренда, необходимо выявить тип тенденции, а эта задача не является чисто математической. Наличие колебаний уровней крайне усложняет выявление типа тенденции и требует всестороннего подхода к этой проблеме, качественного изучения характера развития объекта. При этом нужно дать ответы на такие вопросы:
1. Были ли условия для развития объекта достаточно однородными в изучаемый период?
2. Каков характер действия основных факторов развития?
3. Не произошло ли качественное, существенное изменение условий развития объекта внутри изучаемого периода времени?
Если, например, часть периода предприятие работало по старой технологии, а затем произошло техническое перевооружение — введены новые цехи, поточные линии, то единой тенденции показателей за весь период не будет, скорее всего нужна "периодизация" ряда, т.е. его дробление на отдельные подпериоды: до реконструкции, во время таковой (если она длительна) и после освоения новой технологии.
Чем крупнее изучаемая система, чем больше факторов влияют на динамику изучаемого признака, тем реже возможны резкие, скачкообразные изменения в ряду динамики (не колебания, а именно изменения в тенденции). Большие и сложные системы обладают значительной инерцией, и для скачкообразного, резкого изменения тенденции такой системы требуются большие затраты ресурсов, которые общество выделить не в состоянии. Поэтому такое коренное изменение в экономике, как переход от командно-административного планирования хозяйства к рыночной регулируемой экономике, в масштабе нашей страны неизбежно займет достаточно большое время, за которое сформируются новые тенденции народно-хозяйственных показателей. Для того чтобы разглядеть эти новые тенденции, понадобится время.
Напротив, в масштабе отдельных предприятий вполне возможны резкие изменения, переходы от одной тенденции к другой
Рассмотрим некоторые основные типы уравнений тренда, выражающие те или иные качественные свойства развития.
1. Линейная форма тренда:
![]()
Линейный тренд хорошо отражает тенденцию изменений при действии множества разнообразных факторов, изменяющихся различным образом по разным закономерностям. Равнодействующая этих факторов при взаимопогашении особенностей отдельных факторов (ускорение, замедление, нелинейность) часто выражается в примерно постоянной абсолютной скорости изменения, т.е. в прямолинейном тренде. Таковы, например, тенденции динамики урожайности для масштаба области, республики, крупного региона, страны в целом.
2. Параболическая форма тренда:
![]()
Параболическая форма тренда выражает ускоренное или замедленное изменение уровней ряда с постоянным ускорением. Такой характер развития можно ожидать при наличии важных факторов прогрессивного развития (прогрессирующее поступление нового высокопроизводительного оборудования, увеличение среднесуточного прироста живого веса поросят с возрастом и т.п.). Ускоренное возрастание может происходить в период после снятия каких-то сдерживающих развитие преград — ограничений в распределении дохода, в уровне оплаты труда, при повышении цены на дефицитную продукцию.
Параболическая форма тренда с отрицательным ускорением приводит со временем не только к приостановке роста уровня, но и к его снижению со все большей скоростью. Такой характер развития может быть свойствен производству устаревшей продукции, ликвидируемой отрасли сельского хозяйства на предприятии (ферме) и т.п.
Парабола 2-го порядка (квадратическая) имеет либо максимум (если а2 < 0 и а1 > 0), либо минимум (а1< О, а2> 0). Для нахождения экстремума производную параболы по времени следует приравнять нулю и решить полученное уравнение относительно 1.
3. Экспоненциальная форма тренда:
![]()
где c и b — константы,
e — основание натурального логарифма.
4. Логарифмическая форма тренда:
![]()
где c и b — константы,
ln — функция натурального логарифма
Логарифмический тренд пригоден для отображения тенденции замедляющегося роста уровней при отсутствии предельно возможного значения. Замедление роста становится все меньше и меньше, и при достаточно большом логарифмическая кривая становится малоотличимой от прямой линии. Логарифмический тренд пригоден для отображения роста спортивных достижение (чем они выше, тем труднее их улучшать), роста производггельности агрегата по мере его освоения и совершенствованы, повышения продуктивности скота или эффективности системы при ее совершенствовании без качественных, коренных преобразований. Экстремума логарифмическая кривая не имеет.
5. Тренд в форме степенной кривой:
![]()
где c и b— константы.
Степенная форма —гибкая, пригодная для отображения изменений с разной мерой пропорциональности изменений во времени. Жестким условием является обязательное прохождение через начало координат.
6. Гиперболическая форда тренда:
![]()
Если а1 > 0, гиперболический тренд соответствует тенденции замедляющегося снижения уровня, стремящегося к пределу а. Если а1< 0, тренд выражает тенденцию замедляющегося роста уровней, стремящихся в пределу а. Следовательно, гиперболическая форма тренда подходит для отображения тенденции, процессов, ограниченных предельным значением уровня (предельным коэффициентом полезного действия двигателя, пределом 100%-ной грамотности населения и т.п.).
После теоретического исследования особенностей разных форм тренда необходимо обратиться к фактическому ряду динамики, тем более что далеко не всегда можно надежно установить, какой должна быть форма тренда из чисто теоретических соображений. По фактическому динамическому ряду тип тренда устанавливают на основе графического изображения, путем осреднения показателей динамики, на основе статистической проверки гипотезы о постоянстве параметра тренда.
Более обоснованным приемом выявления тренда является проверка статистической гипотезы о постоянстве того или иного показателя динамики.
Методика анализа и прогнозирования тоже имеет значение. Она определяет степень полноты извлечения информации, содержащейся в исходном ряду динамики. С помощью методики многократного выравнивания удается более полно извлечь информацию о тренде и уменьшить среднюю ошибку прогноза его положения в прогнозируемом периоде. Однако главной составляющей ошибки прогноза конкретного уровня в расчете является не ошибка прогноза положения тренда, а колеблемость уровней около тренда. Поэтому ошибка прогноза конкретного уровня незначительно сократилась за счет многократного выравнивания. При слабой колеблемости уровней и прогнозировании на значительное удаление от базы главную роль станет играть ошибка положения тренда. Тогда многократное выравнивание даст значительное сокращение средней ошибки прогноза конкретных уровней. Но в любом случае эта ошибка всегда больше показателя колеблемости уровней — среднего квадратического отклонения.
При выборе прогнозирующей функции предпочтение отдается той аналитической форме, которая обеспечивает минимальное из стандартных отклонений как погрешность оценки аппроксимации. Поэтому если нет уверенности, что тот или иной вид прогнозирующей функции заведомо предпочтительнее других, то следует испытать несколько различных форм прогнозирующей функции и выбрать наилучшую в соответствии с критерием минимизации стандартного отклонения.
Для прогноза финансово-экономического состояния ОАО "Звенигородский сыроробний комбинат" проанализируем выручку от реализации готовой продукции за предыдущие 2002-2003 годы и составим прогноз на краткосрочный период времени.
Таблица 2.1 – Анализ выручки от реализации продукции
| t | Выручка от реализации продукции 2002-2003 гг тыс.грн | 3-х членные скользящие суммы | 3-х членные скользяшие средние |
| янв.02 | 2276,68 | ||
| фев.02 | 2211,79 | 6500,78 | 2166,93 |
| мар.02 | 2012,30 | 6599,21 | 2199,74 |
| апр.02 | 2375,12 | 6740,81 | 2246,94 |
| май.02 | 2353,39 | 7142,20 | 2380,73 |
| июн.02 | 2413,69 | 7167,45 | 2389,15 |
| июл.02 | 2400,37 | 7227,10 | 2409,03 |
| авг.02 | 2413,04 | 6954,71 | 2318,24 |
| сен.02 | 2141,30 | 7015,91 | 2338,64 |
| окт.02 | 2461,57 | 6967,65 | 2322,55 |
| ноя.02 | 2364,78 | 7283,65 | 2427,88 |
| дек.02 | 2457,30 | 7301,28 | 2433,76 |
| янв.03 | 2479,20 | 7664,93 | 2554,98 |
| фев.03 | 2728,43 | 7756,57 | 2585,52 |
| мар.03 | 2548,93 | 7894,47 | 2631,49 |
| апр.03 | 2617,10 | 8121,22 | 2707,07 |
| май.03 | 2955,18 | 8537,09 | 2845,70 |
| июн.03 | 2964,80 | 8934,18 | 2978,06 |
| июл.03 | 3014,20 | 8714,10 | 2904,70 |
| авг.03 | 2735,10 | 8594,42 | 2864,81 |
| сен.03 | 2845,12 | 8735,12 | 2911,71 |
| окт.03 | 3154,90 | 9165,82 | 3055,27 |
| ноя.03 | 3165,80 | 9483,70 | 3161,23 |
| дек.03 | 3163,00 |
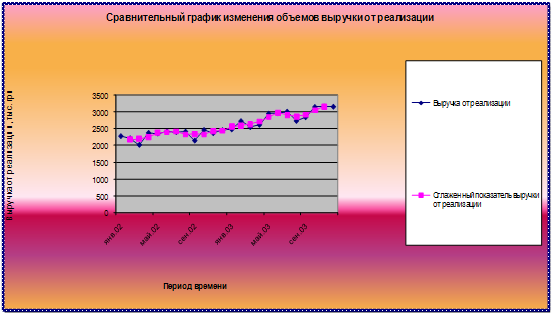
Рисунок 2.1 – Сравнительный график изменения объёмов выручки от реализации
Среднее значение выручки от реализации за 2002 год составило 2323,44 тыс. грн., а среднее значение выручки от реализации за 2003 год составило 2864,31 тыс. грн. Таким образом, разница в среднегодовой цене составила 540,87 тыс. грн. и можно говорить о том, что наблюдается тенденция постоянного роста выручки от реализации.
Поскольку диапазон колебания выручки от реализации в рассматриваемый период достаточно велик (от 2012,30 тыс. грн. в марте 2002 года до 3163 тыс. грн. в декабре 2003 года), необходимо сгладить временной ряд скользящей средней (рис.2.1).
Используя встроенную функцию СТАНДОТКЛОНП приложения EXCEL, находим стандартное отклонение скользящих средних и выручки от реализации.
Стандартное отклонение — это мера того, насколько широко разбросаны точки данных относительно их среднего. Оно равно 292,14 тыс. грн. для генеральной выборки скользящих средних и 330,02 тыс. грн. для генеральной выборки цен.
Функция СТАНДОТКЛОНП предполагает, что аргументы образуют всю генеральную совокупность.
Стандартное отклонение вычисляется с использование "смещенного" или "n" метода.
Для того, чтобы определить с определенным уровнем достоверности величину выручки от реализации готовой продукции определим величину доверительного интервала. Доверительный интервал — это интервал с обеих сторон от среднего выборки.
Для его вычисления, используется функция ДОВЕРИТ. Доверительный интервал для среднего генеральной совокупности равняется 122,07 тыс. грн, т.е. при прогнозе величина цены может изменяться на 122,07 тыс. грн. в большую или меньшую стороны.
Для нахождения наиболее адекватного уравнения тренда используется инстумент "Подбор линии тренда" из мастера диаграмм Microsoft Excel. Результаты подбора уравнения приведены в таблице 2.
Таблица 2.2 – Результаты подбора уравнений
| Вид уравнения | Уравнение | Коэффициент детерминации |
| Линейное | у =44,113х+2076,1 | 0,9177 |
| Логарифмическое | у=306,48ln(x)+1908,1 | 0,7101 |
| Полином 2-го порядка | y = 1,3548x2 + 12,953x + 2200,7 | 0,9454 |
| Полином 3-го порядка | y = -0,0228x3 + 2,2098x2 + 1,2036x + 2213 | 0,9457 |
| Полином 4-го порядка | y = -0,0256x4 + 1,1537x3 - 15,524x2 + 100,68x + 2085,3 | 0,9546 |
| Степенное | у =1973,4х0,1164 | 0,7407 |
| Экспоненциальное | у = 2113,4е0,0160х | 0,9273 |
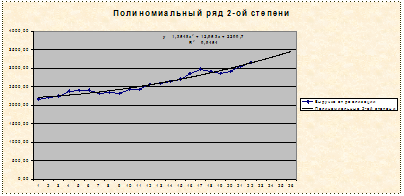 |
Рисунок 2.3 – Полиномиальный ряд 2-ой степени

Рисунок 2.4 – Полиномиальный ряд 3-ей степени
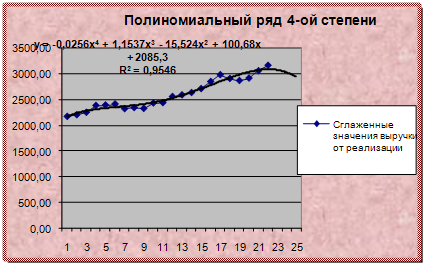
Рисунок 2.5 – Полиномиальный ряд 4-ой степени
Принимая во внимание физическую сущность изучаемого процесса и результаты проведенного аналитического выравнивания, в качестве математической модели тренда выбираем полином 3-го порядка. Таким образом, развитие изучаемого признака происходит с переменным ускорением – развитие при переменном увеличении темпа прироста уровней временного ряда.
По выбранному тренду составляется прогноз, который вычисляется по следующим формулам:
![]() =a0+a1(T+1)+a2(T+1)2+a3(T+1)3,
=a0+a1(T+1)+a2(T+1)2+a3(T+1)3,
![]() = a0+a1(T+2)+a2(T+2)2+a3(T+2)3,
= a0+a1(T+2)+a2(T+2)2+a3(T+2)3,
![]() = a0+a1(T+3)+a2(T+3)2+a3(T+3)3,
= a0+a1(T+3)+a2(T+3)2+a3(T+3)3,
где ai , i=1,2,3-оценки коэффициентов выбранного полиномиального тренда;
Т – период времени.
В результате проведенный вычислений получены следующие данные: в январе 2004 года выручка от реализации готовой продукции ОАО "Звенигородский сыроробний комбинат" будет составлять 3199,544 тыс. грн. (с учетом доверительного интервала от 3077,47 до 3321,6 тыс. грн. ), в феврале – 3267,96 тыс. грн. (с учетом доверительного интервала от 3145,88 до 3390 тыс. грн.), а в марте - 3337,38 тыс. грн. (с учетом доверительного интервала от 3215,31 до 3459,5 тыс. грн. ). Таким образом, в первом квартале 2004 года намечается увеличение цен на продукцию ОАО "Звенигородский сыроробний комбинат".
Чтобы планировать выпуск продукции, для начала нужно знать дифференциацию товаров. Товары бывают потребительские и производственного назначения. Их можно разделить:
По степени готовности к использованию:
· исходные материалы и сырье
По количеству субъектов потребления:
· массовые товары
По степени сложности продажи товара:
· товары, продажа которых не представляет трудности
По затратам времени на приобретения товара:
· товары постоянного спроса
По степени интереса проявляемого к товару:
· товары, к которым проявляется низкий интерес
· товары, к которым проявляется высокий интерес
Для того, чтобы рассчитать оптимальный выпуск продукции с целью максимизации прибыли ОАО "Звенигородский сыркомбинат" была составлена оптимизационная модель линейного программирования, которая решается с помощью функции "Поиск решения" Microsoft Excel.
3 "ИНФОРМАЦИОННАЯ СИТЕМА"
3.1 Разработка информационной системы с помощью редактора Visual Basic.
Информационная система на тему: "Оптимальное планирование выпуска продукции ОАО "Звенигородского сыркомбината", предназначена для использования планирования выпуска продукции.
Информационная система включает в себя:
§ Заставку;
§ Основную управляющую форму (главное меню);
§ Основные разработанные и представленные на рабочих листах подсистемы информационной системы в виде графиков, таблиц;
§ Элементы информационной системы объединены с помощью пользовательского интерфейса.
Информационная система включает в себя такие подсистемы:
Финансово-экономические показатели, которые в свою очередь представлены как: факторный анализ, анализ использования прибыли, анализ финансового состояния и финансово-экономический анализ, а также экономико-математическую модель. Экономико-математическая модель включает в себя: прогнозирование и оптимизационную модель. Подсистемы в свою очередь предназначены для предоставления наиболее оперативной и важной информации.
Так как информационная система включает в себя подсистему с финансово-экономическими показателями, необходимо более подробней описать их предназначение.
Факторный анализ осуществляется с помощью прогноза прибыли предприятия образования и использования фондов, которые формируются за счет прибыли.
Базой для анализа балансовой прибыли предприятия служит сумма балансовой прибыли, зафиксированная в бизнес-плане, а именно – в балансе доходов и расходов, то есть финансовом плане предприятия. Использование бизнес-плановых показателей относительно получения балансовой прибыли анализируется по его составным частям: прибыли от реализации основной продукции, прибыли от другой реализации, прибылей от внереализационных операций (с выделением таких, которые не связанны с основной деятельностью предприятия).
Анализ использования прибыли.
Эффективность работы предприятия в значительной мере зависит от качества управленческих решений, которые касаются использования полученной прибыли. Принимая эти решения, руководство предприятия должно всесторонне взвесить направления первоочередных вложений, финансовых ресурсов, исходя из финансового состояния предприятия, уровня его материально-технической базы, социального развития коллектива, возможностей прибыльного размещения средств на рынке ценных бумаг, в денежно-кредитной сфере и т.п.
Анализ финансового состояния.
Функционируя в рыночной экономике как субъект предпринимательской деятельности, предприятие может обеспечивать такое состояние своих финансовых ресурсов, при котором оно бы стабильно сохраняло возможность беспрерывно использовать свои финансовые обязательства перед своими деловыми партнерами, государством, собственниками, наемными работниками. Приобретая в рыночных условиях не представленную, а настоящую финансовую независимость, неся реальную финансовую ответственность за эффективность хозяйствования и за своевременное исполнение финансовых обязательств, предприятие способно достичь стабильности лишь при строгом соблюдении принципов коммерческого счета, главным среди которых, является сопоставление затрат и результатов, получение максимальной прибыли используя минимальные затраты. Именно это условие является определенным для финансового состояния предприятия.
Финансово-экономический анализ: включает в себя анализ использования прибыли предприятия, факторный анализ балансовой прибыли, ликвидность и платежеспособность предприятия, анализ финансового состояния и анализ финансовой устойчивости предприятия.
Экономико-математическая модель включает в себя прогнозирование и оптимизационную модель.
В подсистеме прогнозирование предсказываются хозяйственные решения, принимающие в текущий момент времени.
В подсистеме экономико-математическая модель представлена оптимизационная модель планирования выпуска продукции.
0 комментариев