Решение задачи с помощью MS Excel
Нелинейные модели регрессии и их линеаризация
Множественная регрессия
Оценка параметров уравнения множественной регрессии
Построение уравнения регрессии в стандартизованном масштабе
Определение совокупного коэффициента корреляции через матрицу парных коэффициентов корреляции
Навигация
Решение задачи с помощью MS Excel
Парная и множественная регрессия и корреляция
19930
знаков
9
таблиц
16
изображений
1.2 Решение задачи с помощью MS Excel
1.2.1 Параметры линейной регрессии
можно определить с помощью встроенной статистической функции ЛИНЕЙН MS Excel. Порядок вычисления следующий:
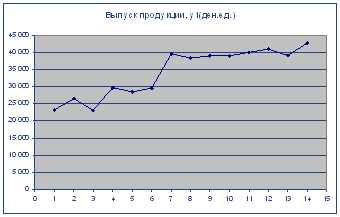
1) ввожу исходные данные (рисунок 1).
2) выделяю область пустых ячеек 5´2 (5 строк, 2 столбца) с целью вывода результатов регрессионной статистики или область 1´2 – для получения только оценок коэффициентов регрессии;
3) активизирую Мастер функций любым из способов:
а) в главном меню выбираю Вставка / Функция;
б) на панели инструментов Стандартная щелкаю по кнопке Вставка функции;
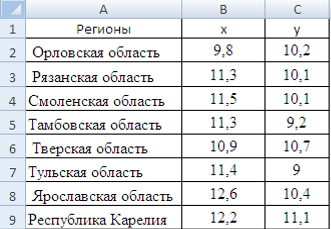
Рисунок 1 Ввод данных для корреляционно-регрессионного анализа
4) в окне «Категория» выбераю Статистические, в окне «Функция» – ЛИНЕЙН. Щелкаю по кнопке ОК (рисунок 2);
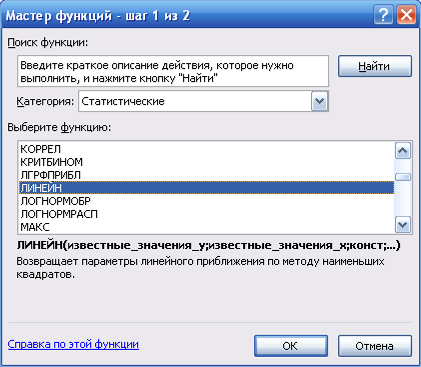
Рисунок 2 Диалоговое окно Мастер функций
5) заполняю аргументы функции (рисунок 3):
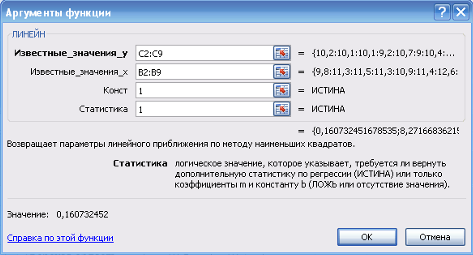
Рисунок 3 Диалоговое окно Аргументы функции
Щелкаю по кнопке ОК;
6) в левой верхней ячейке выделенной области появился первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажимаю на клавишу <F2>, а затем – на комбинацию клавиш <CTRL> + <SHIFT> + <ENTER>.
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
| Значение коэффициента b | Значение коэффициента a |
| Среднеквадратическое отклонение b | Среднеквадратическое отклонение a |
| Коэффициент детерминации R2 | Среднеквадратическое отклонение y |
| F – статистика | Число степеней свободы |
| Регрессионная сумма квадратов | Остаточная сумма квадратов |
Результаты вычислений функции ЛИНЕЙН представлены на рисунке 4.
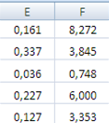
Рисунок 4 Результаты вычислений функции ЛИНЕЙН
1.2.2 С помощью инструмента анализа данных Регрессия, помимо результатов регрессионной статистики, дисперсионного анализа и доверительных интервалов, можно получить остатки и графики подбора линии регрессии, остатков и нормальной вероятности. Порядок действий следующий:
1) проверяю доступ к пакету анализа. В главном меню последовательно выбераю Сервис / Настройки. Устанавливаю флажок Пакет анализа;
2) в главном меню выбираю Сервис / Анализ данных / Регрессия. Щелкаю по кнопке ОК;
3) после вызова режима Регрессия на экране появляется диалоговое окно (рисунок 5), в котором задаются следующие параметры:
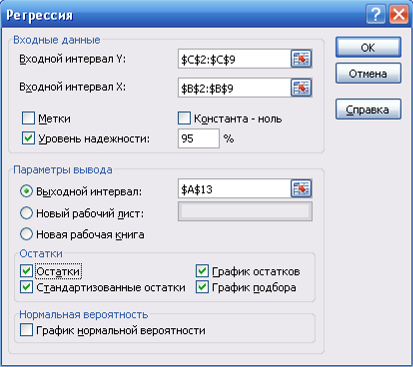
Рисунок 5 Диалоговое окно режима Регрессия
Результаты регрессионного анализа для исходных данных представлены на рисунке 6.
Вывод итогов
| Регрессионная статистика | |
| Множественный R | 0,19101862 |
| R-квадрат | 0,03648811 |
| Нормированный R-квадрат | -0,1240972 |
| Стандартная ошибка | 0,74755394 |
| Наблюдения | 8 |
Дисперсионный анализ
| df | SS | MS | F | Значимость F | |
| Регрессия | 1 | 0,12697864 | 0,126978637 | 0,2272195 | 0,6504571 |
| Остаток | 6 | 3,35302136 | 0,558836894 | ||
| Итого | 7 | 3,48 |
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 8,271668362 | 3,844685341 | 2,151455224 | 0,07495556 | 1,135937744 | 17,67927447 |
| Переменная X 1 | 0,160732452 | 0,337194727 | 0,476675461 | 0,6504571 | 0,664353319 | 0,985818223 |
Вывод остатка
| Наблюдение | Предсказанное Y | Остатки | Стандартные остатки |
| 1 | 9,846846389 | 0,353153611 | 0,510263509 |
| 2 | 10,08794507 | 0,012054934 | 0,017417896 |
| 3 | 10,12009156 | -0,020091556 | -0,029029827 |
| 4 | 10,08794507 | -0,887945066 | -1,28297135 |
| 5 | 10,02365209 | 0,676347915 | 0,977239505 |
| 6 | 10,10401831 | -1,104018311 | -1,595170599 |
| 7 | 10,29689725 | 0,103102747 | 0,148970781 |
| 8 | 10,23260427 | 0,867395727 | 1,253280084 |
Похожие работы
... и все коэффициенты корреляции равны 1, то определитель такой матрицы равен 0: . Чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И наоборот, чем ближе к 1 определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов. Проверка мультиколлинеарности факторов может быть ...
... 7,33 1965 81,0 7,52 1966 83,0 7,62 1967 85,4 7,72 1968 85,9 7,89 1969 85,9 7,98 1970 87,0 8,03 1971 90,2 8,21 1972 92,6 8,53 1973 95,0 8,55 1974 93,3 8,28 1975 95,5 8,12 Найдем параметры линейного уравнения множественной регрессии и значения остатков. Дополним таблицу данных столбцами "", "Квадрат разности остатков " и "Квадрат остатка " и заполним их. Таблица ...
... t-критерий Стъюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Но о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью f-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки: Оценка значимости коэффициентов чистой регрессии с помощью /-критерия ...
... взяты за 2003 год. Данные взяты из статистического сборника Регионы России Социально-экономические показатели. 2003. Федеральная служба государственной статистики Построение модели множественной регрессии Расчет параметров Рассчитаем необходимые параметры: Признак Ср. знач. СКО Характеристики тесноты связи βi bi Коэф-ты частной корр. F-критерий фактический ...
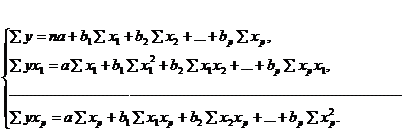
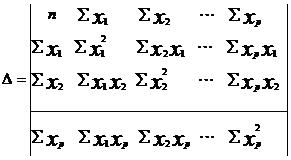
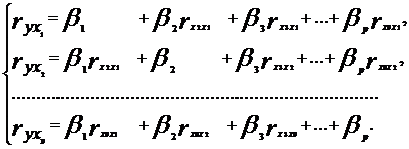
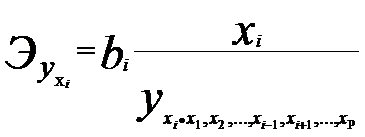
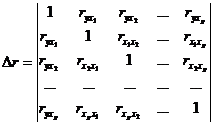
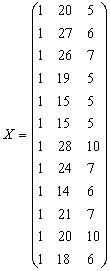
0 комментариев