Решение задачи с помощью MS Excel
Нелинейные модели регрессии и их линеаризация
Множественная регрессия
Оценка параметров уравнения множественной регрессии
Построение уравнения регрессии в стандартизованном масштабе
Определение совокупного коэффициента корреляции через матрицу парных коэффициентов корреляции
Навигация
Нелинейные модели регрессии и их линеаризация
Парная и множественная регрессия и корреляция
19930
знаков
9
таблиц
16
изображений
2. Нелинейные модели регрессии и их линеаризация
Цель работы: ознакомиться с методикой расчета показателей парной нелинейной регрессии и корреляции, овладеть приемами построения нелинейных регрессионных моделей с помощью MS Exсel.
РЕШЕНИЕ:
2.1.1 Регрессия в виде степенной функции имеет вид:
.
Для оценки параметров модели линеаризую (привожу к линейному виду) модель путем логарифмирования: 
.
Обозначаю lny =Y, lna =A, lnx =X.
Тогда получаю: Y=A+bX.
Для расчетов составляю с помощью MS Excel вспомогательную таблицу, в которой рассчитаю натуральные логарифмы с помощью математической функции LN (рисунок 7).
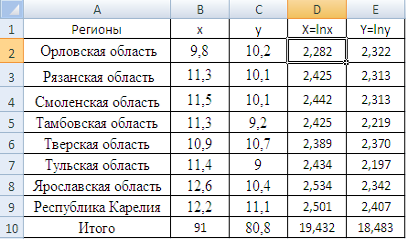
Рисунок 7 Расчет натуральных логарифмов
Далее с помощью инструмента Регрессия рассчитываю параметры уравнения (рисунки 8, 9).
Рисунок 8 Диалоговое окно Регрессия
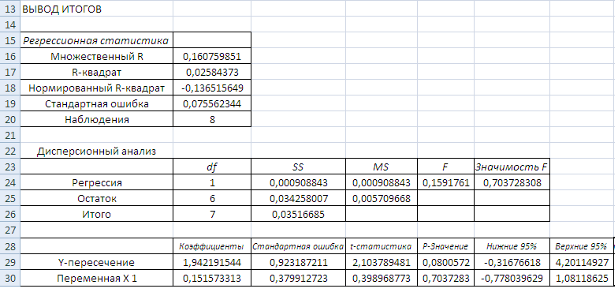
Рисунок 9 Результаты расчета параметров степенной функции
Таким образом, уравнение регрессии имеет вид:
.
Выполнив потенцирование, получим:
.
Параметр b=0,151 означает коэффициент эластичности, который показывает, что с ростом величины среднедушевых доходов населения на 1% общий коэффициент рождаемости увеличится в среднем на 0,151%.
2.1.2 Регрессия в виде экспоненты имеет вид:
. (13)
Для оценки ее параметров необходимо привести уравнение к линейному виду:
.
Для расчета параметров экспоненциальной прямой можно воспользоваться статистической функцией ЛГРФПРИБЛ MS Excel. Результаты вычислений представлены на рисунке 10.
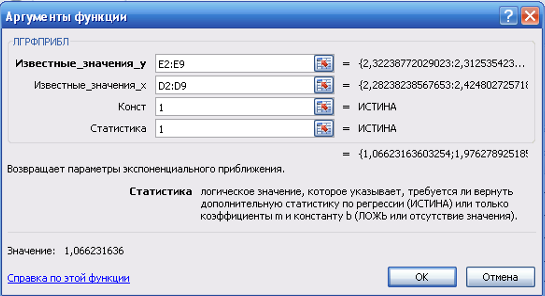
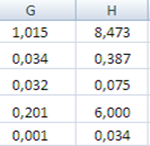
Рисунок 10 Результаты вычислений параметров экспоненциальной функции
Таким образом, уравнение регрессии в виде экспоненты имеет вид:
.
2.1.3 Регрессия в виде равносторонней гиперболы имеет вид:
,
чтобы оценить параметры a и b, привожу модель к линейному виду, заменив
.
Тогда
.
Результаты замены представлены на рисунке 11.
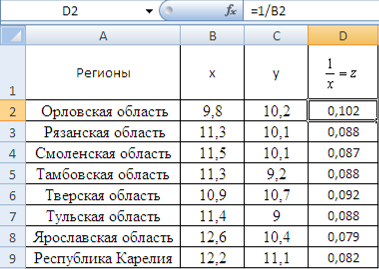
Рисунок 11 Вспомогательная таблица для расчета параметров гиперболы
Далее с помощью инструмента Регрессия рассчитываю параметры уравнения. Результаты расчета представлены на рисунке 12.
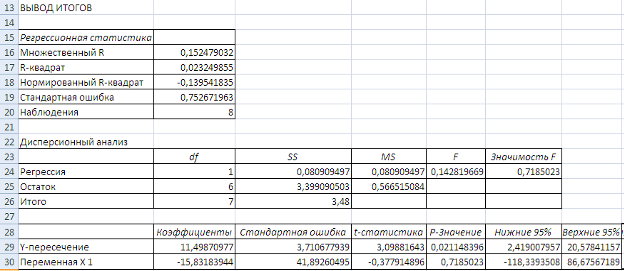
Рисунок 12 Результаты вычислений параметров гиперболической функции
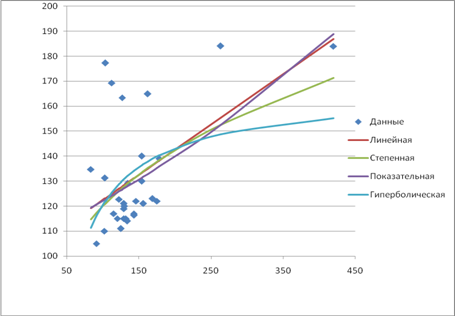
Выберем наилучшую модель, для чего объединим результаты построения парных регрессий в одной таблице 3.
Все уравнения регрессии достаточно хорошо описывают исходные данные.
Таблица 3 Результаты корреляционно-регрессионного анализа
| Уравнение регрессии | Коэффициент корреляции | Коэффициент детерминации | F-критерий Фишера |
|
| 0,659 | 0,036 | 0,227 |
|
| 0,161 | 0,026 | 0,159 |
|
| 0,179 | 0,032 | 0,201 |
|
| 0,152 | 0,023 | 0,143 |
Предпочтение можно отдать линейной функции, для которой значения коэффициентов корреляции и детерминации и F-критериев Фишера наибольшие.
Похожие работы
... и все коэффициенты корреляции равны 1, то определитель такой матрицы равен 0: . Чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И наоборот, чем ближе к 1 определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов. Проверка мультиколлинеарности факторов может быть ...
... 7,33 1965 81,0 7,52 1966 83,0 7,62 1967 85,4 7,72 1968 85,9 7,89 1969 85,9 7,98 1970 87,0 8,03 1971 90,2 8,21 1972 92,6 8,53 1973 95,0 8,55 1974 93,3 8,28 1975 95,5 8,12 Найдем параметры линейного уравнения множественной регрессии и значения остатков. Дополним таблицу данных столбцами "", "Квадрат разности остатков " и "Квадрат остатка " и заполним их. Таблица ...
... t-критерий Стъюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Но о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью f-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки: Оценка значимости коэффициентов чистой регрессии с помощью /-критерия ...
... взяты за 2003 год. Данные взяты из статистического сборника Регионы России Социально-экономические показатели. 2003. Федеральная служба государственной статистики Построение модели множественной регрессии Расчет параметров Рассчитаем необходимые параметры: Признак Ср. знач. СКО Характеристики тесноты связи βi bi Коэф-ты частной корр. F-критерий фактический ...
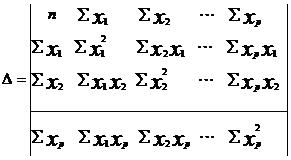
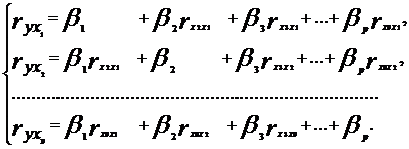
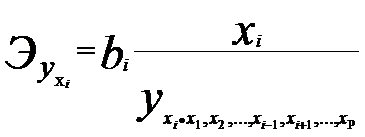
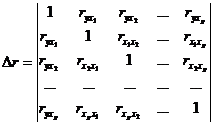
0 комментариев