Решение задачи с помощью MS Excel
Нелинейные модели регрессии и их линеаризация
Множественная регрессия
Оценка параметров уравнения множественной регрессии
Построение уравнения регрессии в стандартизованном масштабе
Определение совокупного коэффициента корреляции через матрицу парных коэффициентов корреляции
Навигация
Оценка параметров уравнения множественной регрессии
Парная и множественная регрессия и корреляция
19930
знаков
9
таблиц
16
изображений
4. Оценка параметров уравнения множественной регрессии
4.1 Оценка параметров с помощью метода определителей
Параметры уравнения множественной регрессии оцениваются, как и в парной регрессии, методом наименьших квадратов (МНК). При его применении строится система нормальных уравнений, решение которой и позволяет получить оценки параметров регрессии.
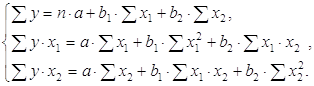
Для оценки параметров уравнения множественной регрессии построим с помощью MS Excel вспомогательную таблицу 2.
Таблица 2 Вспомогательная таблица для расчета параметров уравнения множественной регрессии
| № |
|
|
|
|
|
|
|
|
|
| 1 | 7,2 | 19,9 | 9,6 | 51,8 | 143,28 | 396,01 | 69,12 | 191,04 | 92,16 |
| 2 | 8,1 | 17,1 | 9,4 | 65,6 | 138,51 | 292,41 | 76,14 | 160,74 | 88,36 |
| 3 | 8,4 | 17,4 | 9,6 | 70,6 | 146,16 | 302,76 | 80,64 | 167,04 | 92,16 |
| 4 | 8,6 | 13,5 | 8,9 | 74 | 116,1 | 182,25 | 76,54 | 120,15 | 79,21 |
| 5 | 8,6 | 14,8 | 10,2 | 74 | 127,28 | 219,04 | 87,72 | 150,96 | 104,04 |
| 6 | 8,4 | 14,2 | 8,4 | 70,6 | 119,28 | 201,64 | 70,56 | 119,28 | 70,56 |
| 7 | 9,9 | 15,1 | 9,9 | 98 | 149,49 | 228,01 | 98,01 | 149,49 | 98,01 |
| 8 | 10,1 | 17 | 10,6 | 102 | 171,7 | 289 | 107,06 | 180,2 | 112,36 |
| 9 | 16,2 | 14,5 | 11,9 | 262 | 234,9 | 210,25 | 192,78 | 172,55 | 141,61 |
| 10 | 11,6 | 16,1 | 11,9 | 135 | 186,76 | 259,21 | 138,04 | 191,59 | 141,61 |
| 11 | 10,5 | 14,8 | 11,6 | 110 | 155,4 | 219,04 | 121,8 | 171,68 | 134,56 |
| 12 | 11,4 | 12,4 | 10,9 | 130 | 141,36 | 153,76 | 124,26 | 135,16 | 118,81 |
| 13 | 10,6 | 12,6 | 8,3 | 112 | 133,56 | 158,76 | 87,98 | 104,58 | 68,89 |
| 14 | 15,2 | 15,5 | 10,3 | 231 | 235,6 | 240,25 | 156,56 | 159,65 | 106,09 |
| 15 | 8,6 | 20,3 | 10,7 | 74 | 174,58 | 412,09 | 92,02 | 217,21 | 114,49 |
| 16 | 7,9 | 17,1 | 9,7 | 62,4 | 135,09 | 292,41 | 76,63 | 165,87 | 94,09 |
| 17 | 5,8 | 30,4 | 11,8 | 33,6 | 176,32 | 924,16 | 68,44 | 358,72 | 139,24 |
| 18 | 8 | 13,8 | 17 | 64 | 110,4 | 190,44 | 136 | 234,6 | 289 |
| 19 | 4 | 44,8 | 16,7 | 16 | 179,2 | 2007 | 66,8 | 748,16 | 278,89 |
| 20 | 6,6 | 18,3 | 12,8 | 43,6 | 120,78 | 334,89 | 84,48 | 234,24 | 163,84 |
| 21 | 4,5 | 44,2 | 14,5 | 20,3 | 198,9 | 1953,6 | 65,25 | 640,9 | 210,25 |
| 22 | 6,9 | 18,3 | 14,2 | 47,6 | 126,27 | 334,89 | 97,98 | 259,86 | 201,64 |
| 23 | 7,9 | 12,9 | 13,6 | 62,4 | 101,91 | 166,41 | 107,44 | 175,44 | 184,96 |
| 24 | 9,8 | 19,2 | 11,3 | 96 | 188,16 | 368,64 | 110,74 | 216,96 | 127,69 |
| Итого | 214,8 | 454,2 | 273,8 | 2107 | 3711 | 10337 | 2393 | 5426,07 | 3252,5 |
| Среднее | 8,592 | 18,2 | 10,95 | 84,3 | 148,44 | 413,48 | 95,72 | 217,043 | 130,1 |
На основе расчетов, представленных в таблице 2, получили следующую систему:
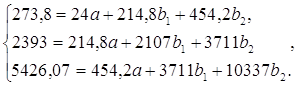
Решаем систему с помощью метода определителей. При этом:
где 
− определитель системы;
− частные определители.
В результате расчета определителей получили следующие значения:
∆=4702879,56;
∆а=45336681,238,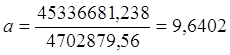 
,
∆b1=–326370,8088,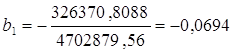 
,
∆b2=593730,7872,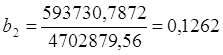 
.
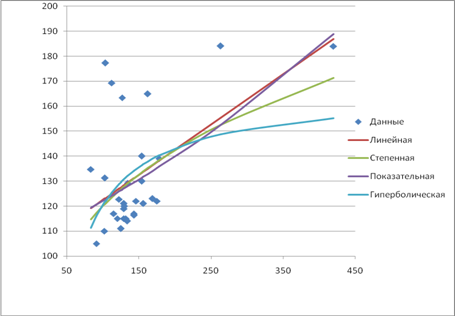
Уравнение множественной регрессии имеет вид:
=9,6402-0,0694х1+0,1262х2.
Таким образом, при увеличении уровня бедности на 1%, общий коэффициент рождаемости в изучаемых регионах снизится на 0,0694 раз, а при увеличении среднедушевого дохода на 1000 руб., общий коэффициент рождаемости увеличится на 0,1262 раз.
Похожие работы
... и все коэффициенты корреляции равны 1, то определитель такой матрицы равен 0: . Чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И наоборот, чем ближе к 1 определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов. Проверка мультиколлинеарности факторов может быть ...
... 7,33 1965 81,0 7,52 1966 83,0 7,62 1967 85,4 7,72 1968 85,9 7,89 1969 85,9 7,98 1970 87,0 8,03 1971 90,2 8,21 1972 92,6 8,53 1973 95,0 8,55 1974 93,3 8,28 1975 95,5 8,12 Найдем параметры линейного уравнения множественной регрессии и значения остатков. Дополним таблицу данных столбцами "", "Квадрат разности остатков " и "Квадрат остатка " и заполним их. Таблица ...
... t-критерий Стъюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Но о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью f-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки: Оценка значимости коэффициентов чистой регрессии с помощью /-критерия ...
... взяты за 2003 год. Данные взяты из статистического сборника Регионы России Социально-экономические показатели. 2003. Федеральная служба государственной статистики Построение модели множественной регрессии Расчет параметров Рассчитаем необходимые параметры: Признак Ср. знач. СКО Характеристики тесноты связи βi bi Коэф-ты частной корр. F-критерий фактический ...
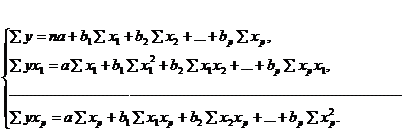
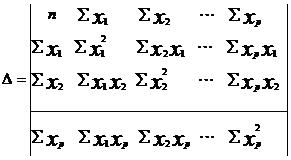
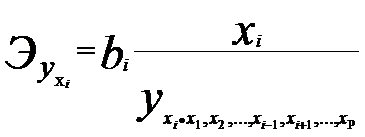
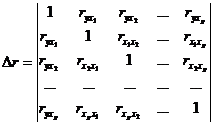
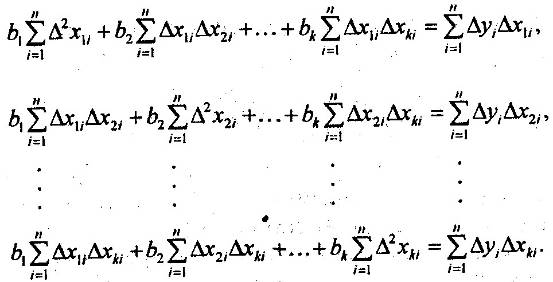
0 комментариев