Структура сервоприводу

1.1  Структура сервоприводу

Сервопривід – частина системи стабілізації (СС), яка призначена для посилення командного сигналу і перетворення його електричної енергії в механічне переміщення. Переміщення залежно від практичного вживання може бути обертальним або поступальним. Таким чином, елекрогідропривод є виконавчим органом СС, що впливає на кермо виробу. Функціональна схема сервоприводу представлена на малюнку 1.1.

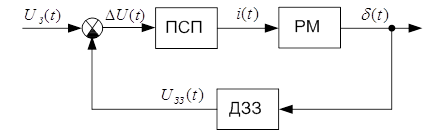
Малюнок 1.1 – Функціональна схема досліджуваної системи сервоприводу

Ця схема застосовується частіше всього на вітчизняних виробах.

ПСП – підсилювач сервоприводу;

РМ – рульова машинка (іноді рульовий агрегат для СС);

ДЗЗ – датчик зворотного зв'язку;

– струм управління рульової машинки;

– струм зворотного зв'язку;

– командний струм;

– результуючий струм, сума струмів  (сумарний струм);

– поворот вихідного валу або переміщення штока РМ.

Іноді використовується схема, яка представлена на мал. 1.2.

Відмінність цієї схеми від попередньої в тому, що тут застосовується механічний зворотний зв'язок (ЗЗ). Такий ЗЗ здійснюється за допомогою важелів або за допомогою редуктора.

Рульова машинка із зворотним зв'язком утворює позиційний привод (ПП).

Така структурна схема використовується переважно на американських ракетах. Ми розглядатимемо вітчизняну схему. Розберемося, що представляють загалом елементи структурної схеми і їх передавальні функції.

1.2  Огляд літератури

Нелінійної називають систему, поведінка якої описується нелінійним рівнянням.

Всі реальні елементи, а отже, і системи, через такі явища, як сухе і в'язке тертя, насичення, нечутливість, гістерезис, пружність, адгезія та ін., є нелінійними. Як образно виразився Я.З. Ципкін, «лінійні системи – це невеликий острівець в безбережному океані нелінійних систем»

Тому теорію лінійних систем можна розглядати тільки як більш менш точну ідеалізацію реальних систем, що не охоплює всієї різноманітності реальних систем і що не враховує багатьох властивих їм явищ.

Нелінійні системи в порівнянні з лінійними володіють цілим рядом особливостей:

1)         на відміну від лінійних в нелінійних системах несправедливий принцип комутативності, тобто від зміни порядку перетворення сигналу може змінитися результат, і не виконується принцип суперпозиції, тобто вихідний сигнал не можна розглядати як суму реакцій системи на окремі складові вхідного сигналу;

2)         форма сигналів в нелінійній системі залежить не тільки від форми вхідного сигналу, але і від його величини. Крім того, характер процесів залежить від величини початкових умов;

3)         в нелінійних системах можливий режим автоколивань, тобто за відсутності у вхідному сигналі гармонійної складової в системі можуть виникнути незгасаючі коливання;

4)         стійкість рівноважного стану лінійної системи визначається її структурою і значеннями параметрів (коефіцієнтів передачі, постійних часу і т. п.). Нелінійна система може мати нескінченну безліч станів стійкої рівноваги і декілька стійких режимів автоколивань. Сталий стан рівноваги або коливальний режим залежать не тільки від структури і параметрів системи, але і від величини вхідного сигналу і початкових умов;

5)         в сталому режимі в лінійних системах частота вихідного сигналу співпадає з частотою вхідного сигналу. В нелінійних системах вихідний сигнал може містити складові, частота яких вище або нижче за частоту вхідного сигналу, тобто гармоніки і субгармоники;

6)         частотні характеристики нелінійних систем залежать не тільки від її структури і параметрів, але і від величини вхідного сигналу і початкових умов;

7)         частотні характеристики нелінійних систем можуть мати розриви безперервності, що приводить до перескока з одного режиму на іншій.

Ці і інші особливості показують, наскільки поведінка нелінійних систем різноманітніше за поведінку лінійних систем.

Якщо нелінійна функція допускає лінійну апроксимацію, у відхилення сигналів від їх необурених значень достатньо малі, з інженерної точки зору допустимо розглядати лінеаризовану систему і використовувати добре розроблений апарат теорії лінійних систем автоматичного управління (САУ).

А якщо нелінійна функція містить злами, розриви або неоднозначності, а також при підвищених вимогах до точності розрахунків застосовують теорію нелінійних САУ.

Нелінійні елементи, що використовуються в САУ, надзвичайно різноманітні і можуть класифікуватися по різних ознаках.

Залежно від ступені впливу у вирішуваній задачі даної нелінійності на поведінку САУ розрізняють істотні і неістотні нелінійності [6].

Нелінійні елементи діляться на природні, неминуче присутні, і штучні спеціально що вводяться в системи для додання їм бажаних властивостей, До першого типу відносяться нелінійні елементи з тертям, зазором (люфтом), гістерезисом, зоною нечутливості, насиченням до іншими явищами, що спотворюють лінійний зв'язок між вихідними і вхідними сигналами. Вплив цих нелінійностей шкідливо, і його звичайно прагнуть зменшити. До другого типу відносяться нелінійні керівники і коректуючі пристрої, що використовують релейні, степенні, показові, логічні та інші функції. Елемент є безінерційним (статичним), якщо він описується рівнянням алгебри або графіком (статичною характеристикою). Елемент, що описується нелінійним диференціальним, різницевий або інтегральним рівнянням, володіє динамічною нелінійністю.

Статичні нелінійності звичайно задаються у вигляді графіків. На малюнку 1.3 показані статичні характеристики, типові, що містять, нелінійності.

Шматково-постійними релейними характеристиками з розривами безперервності (1 – 5) володіють різного виду реле. Характеристику 1 має ідеальне реле,

2 – ідеальне трьохпозиційне реле із зоною нечутливості, 3 – трьохпозиційне реле із зоною нечутливості і з гістерезисом, 4 – двохпозиційне поляризоване реле з гістерезисом, 5 – нейтральне реле із зоною нечутливості і гістерезисом.

Окрім петлевих нелінейностей із гістерезисом, тобто відставанням зміни вихідної величини від зміни вхідної величини, існують петлеві нелінійності з випередженням, спеціально створювані для корекцій динамічних властивостей САУ.

Ступінчастою характеристикою 6 володіє дротяні потенціометри, квантователі сигналу по рівню та ін.

Безперервними шматково-лінійними характеристиками із зломами (7 – 11) апроксимуються нелінійності різних підсилювачів, випрямлячів. Характеристику 7 має підсилювач з насиченням, підсилювач-обмежувач, 8 – підсилювач із зоною нечутливості або порогом спрацьовування і з насиченням, 9 – підсилювач із змінним коефіцієнтом посилення, 10 – ідеальний однополуперіодний випрямляч, 11 – ідеальний двухполуперіодний випрямляч. Нелінійністю типу зазор (12) володіють зубчаті передачі. Механічна передача із зазором, гістерезисом і обмеженням має характеристику 13.

Криволінійні характеристики мають двотактний магнітний підсилювач і частотний детектор (14), електромашинний підсилювач (15), квадратор (16).

Елементи з в'язким тертям (17) і з в'язким тертям і гістерезисом (18) володіють негативним дефектом.

Бінарна (19), синусоїдальна (20), вилоподібна (21) і інші періодичні характеристики властиві фазовим детекторам.

Характеристики I, 2, 6–11, 14, 16, 17, 19–21. є однозначними. Вони дозволяють однозначно визначати величину вихідного сигналу, по відомій величині вхідного сажала.

Характеристики 3, 4, 5, 12, 13, 15, 18 є неоднозначними. Вихідний сигнал елементів з такими характеристиками залежить не тільки від величини вхідного сигналу в даний момент часу, але і від його поведінки в попередні моменти часу:

у(t)=F (x(t)) (1.1)

Крім того, нелінійності бувають симетричними і несиметричними, парними і непарними, гладкими і нерівними.

Дня аналітичного опису статичних нелінійностей часто використовують шматково-лінійну і поліномінальну апроксимації.

Нелінійності, є в будь-якому реальному приводі, можуть істотно впливати на його динамічні властивості, зокрема на стійкість. Цей вплив виявляється в наступному:

Привод, стійкий і має достатній запас стійкості в лінійному наближенні, може виявитися не стійким або не володіючим тим запасом стійкості, який очікується. Такий вплив надають частіше за все «петлеві» нелінійності (люфт, гістерезис), але при деяких положеннях в структурі приводу до цього ж ефекту можуть привести і однозначні нелінійності, наприклад навіть такі, як зона нечутливості [9–10].

В приводі можуть з'явитися принципово нові типи руху, які не можуть існувати в лінійних системах і тому не можуть бути навіть якісно пояснені з позиції лінійної моделі. До таких рухів відносяться в першу чергу автоколивання. Автоколивання можуть викликати ті ж нелінійності, які викликають зменшення запасу стійкості. В одноконтурних системах – це петлеві нелінійності, в неодноконтурних і однозначні.

Допустимі або недопустимі автоколивання в реальній системі – питання дискусійне. Все залежить від їх параметрів, тобто від розмаху і частоти. Одне поза сумнівом автоколивання не повинні порушувати вимоги по точності, отже, якщо їх і можна допустити, то тільки при таких, амплітудах, при яких викликана ними помилка сумісно з вимушеною помилкою, викликаною відтворенням всіх заданих законів управління, не виходить за межі допустимих.

Для достатньо повної думки про динамічні властивості проектованого приводу і його придатності для виконання доручених йому функцій потрібно розглянути і його, нелінійну модель. При цьому розгляді перед інженером виникають дві основні задачі: по-перше, зрозуміти, в чому може виявлятися вплив тієї або іншої нелінійності, зрозуміти фізику дії як окремої нелінійності, так і сукупності декількох нелінійностей і, по-друге, оцінити, кількісний вплив головних нелінійностей на стійкість і динамічну точність досліджуваної системи.

З огляду на те, що на нелінійну систему принцип суперпозиції не розповсюджується, строго кажучи, не можна розглядати вплив кожної нелінійності окремо і потім підсумовувати ефекти їх дії. Тому, здавалося б, потрібно розглядати вплив всіх нелінійностей спільно. Такий підхід пов'язаний із значними обчислювальними труднощами, які, правда, можуть бути подолані при використовуванні сучасних обчислювальних машин. Важливе інше, такий підхід не має сенсу, в усякому разі, на першому етапі проектування нелінійної системи, оскільки не дає корисної інформації про вплив кожної з нелінійностей на динамічні властивості, а отже, не може допомогти у виборі методів цілеспрямованої дії з метою забезпечення необхідних динамічних властивостей.

Частіше всього характер впливу нелінійності не змінюється при її дії в сукупності з іншими, тому має сенс розгляд і окремо взятих нелінійностей, і розумно вибраних комбінацій невеликого числа нелінійностей.

Розуміння впливу нелінійностей на динамічні властивості важливе і для правильного проектування лінійного варіанту – вибору структури, методів корекції і т.п., оскільки системи, еквівалентні по динамічних властивостях в лінійному плані, можуть виявитися зовсім не еквівалентними при обліку нелінійностей і при синтезі лінійної структури раціонально використовувати такі, у яких шкідливий вплив основних нелінійностей на динамічні властивості менше.

Особливістю нелінійного перетворення із зворотним зв'язком є неможливість отримання в явному виді залежності між вхідними і вихідними сигналами.

Тому для отримання статичних характеристик перетвореного сигналу, не можуть бути безпосередньо застосовані.

Дамо короткий опис розроблених в даний час методів дослідження нелінійних перетворень, що не вимагають завдання явної залежності між вхідним і вихідним сигналами.