Розрахунок сервоприводу з нелінійною ланкою

5.2 Розрахунок сервоприводу з нелінійною ланкою

а). Нелінійна ланка задана так (малюнок 5.8)

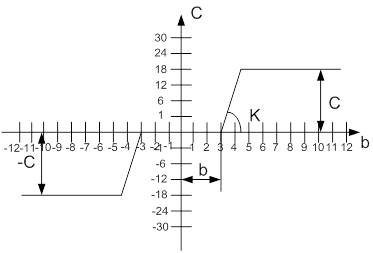
Малюнок 5.8 – Нелінійна ланка

Характеристика нелінійної ланки:

b=3 ма; c=18 ма; K=1;

б). Лінійна частина:

;

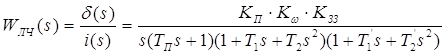З умови технічного завдання дано:

; ; ; ; ;

; ; ;;

;

де Р_СЕР – середній розподіл Гауса

Розрахунок:

1)   Визначимо q_m.

Значення коефіцієнта qдля даного виду нелінійності визначається виразом:

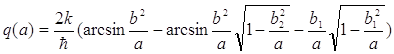(5.3)

де а – амплітуда вхідного сигналу;

.

Дана нелінійність має . Для визначення qm задаємося різними значеннями амплітуди вхідного сигналу, враховуючи, що a>>b₂ і прораховуємо на обчислювальній машині (ОМ) значення коефіцієнта q(а) з кроком.

Результати обчислення заносимо в таблицю 1 в додатку Б.

2). Визначимо K_КР (використовуючи A₀):

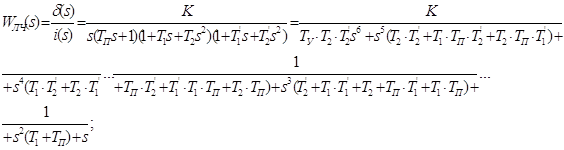
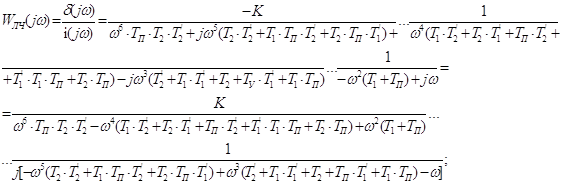
Визначимо з умови:

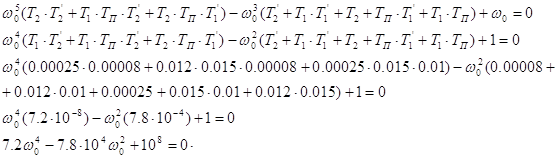
Зробимо заміну:

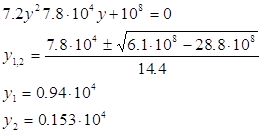
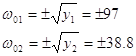
K_КР визначається при . При підстановці в дійсну частину  одержимо A₀. В цьому випадку K=K_КР.

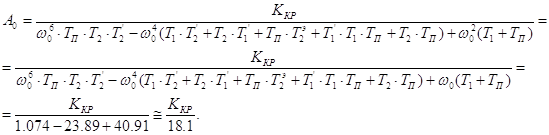
Використовуючи цей результат, запишемо 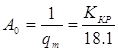:, звідси критичний круговий коефіцієнт сервоприводу рівний:

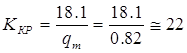
Значення q_m узято з таблиці 2 додатку Б.

3). Визначення номінального значення добротності сервоприводу і коефіцієнта зворотного зв'язку:

а)

б) σ визначаємо з виразу:

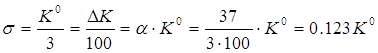
в) номінальне значення добротності визначиться:

г) значення коефіцієнта ЗЗ знайдемо із співвідношення:

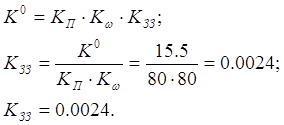
5.3 Облік впливу інерційності сервоприводу на стійкість руху

Приймаємо допущення:

1.   Нелінійності неістотні.

2.   Лінійну частину сервоприводу спростимо до 2-го порядку.

Вважатимемо, що Т_П=0.

Для лінійного сервоприводу 2-го порядку в розімкненому стані:

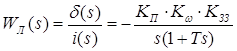(5.4)

Запишемо передавальну функцію сервоприводу:

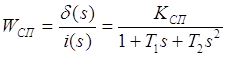(5.5)

де.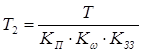

Під керованістю розуміють здатність змінювати параметри свого руху при відхиленні управляючих органів. Керованість напряму пов'язана із стійкість.

Під стійкістю розуміється здатність об'єкту управління повертатися на задану траєкторію після дії на нього обурення.

Динамічними показниками керованості в тимчасовій області вважаються параметри перехідного процесу при східчастому відхиленні управляючих органів час перехідного процесу і величина перерегулювання, в частотній області – власна частота короткоперіодичного руху (ω₀) і відносний коефіцієнт загасання (ξ).

Для перевірки вибраних алгоритмів управління виконаємо моделювання системи з використанням системи моделювання Matlab/Simulink для побудови частотних характеристик. Досліджувана схема моделювання сервоприводу з урахуванням нелінійності приведена на малюнку 5.9.

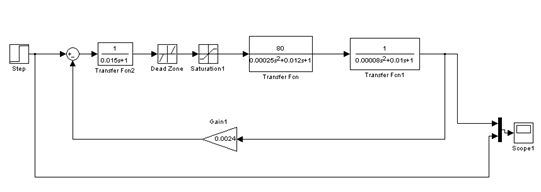
Малюнок 5.9 – Досліджувана схема сервоприводу з урахуванням нелінійності

На малюнку 5.10 представлений перехідною процес досліджуваної системи сервоприводу з урахуванням нелінійності при К_ЗЗ> 0.0024=0.024

Малюнок 5.10 – Перехідної процес досліджуваної системи сервоприводу з урахуванням нелінійності при К_ЗЗ > 0.0024=0.024

З одержаного перехідного процесу видно, що пік амплітуди рівний А=2.5°, немає сталого значення амплітуди і час перехідного процесу дуже великий, т.ч. присутні автоколивання, отже система нестійка, це не задовольняє вимогам ТЗ. Величина перерегулювання складає приблизно δ=1.5% від сталого значення амплітуди і теж не задовольняє вимогам ТЗ.

На малюнку 5.11 представлений перехідною процес досліджуваної системи сервоприводу з урахуванням нелінійності при К_ЗЗ=0.0024.

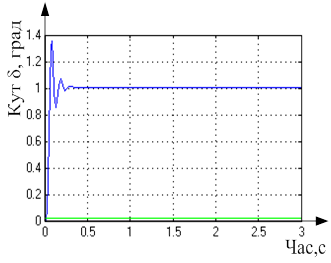
Малюнок 5.11 – Перехідної процес досліджуваної системи сервоприводу з урахуванням нелінійності при К_ЗЗ = 0.0024

На вказаному графіку видно що, що пік амплітуди рівний А=1.39°, стале значення амплітуди, рівний А=1°и час перехідного процесу t_ПП=0,35c, який задовольняє вимогам ТЗ. Величина перерегулювання складає приблизно δ=0.39% від сталого значення амплітуди і задовольняє вимогам ТЗ. Отже можна зробити висновок, що К_ЗЗ розрахований правильно, система стійка.

Побудуємо ЛАЧХ і ЛФЧХ нескоректованої системи (мал. 5.12) за допомогою команд MATLAB/Simulink, а також ЛАЧХ і ЛФЧХ скоректованої системи.

На малюнку 5.12. приведені ЛАЧХ нескоректованої системи і варіант ЛАЧХ скоректованої системи. Верхній графік відображає характеристики розімкненої нескоректованої системи (ЛАЧХ, що розташовується); нижній графік – розімкненої скоректованої системи (бажана ЛАЧХ), також на малюнку приведена фазочастотна характеристика.

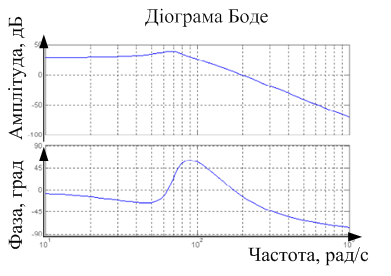
Малюнок 5.12 – ЛАЧХ і ЛФЧХ замкнутої скоректованої системи

Визначимо запас стійкості розімкненої системи по амплітуді і запас стійкості по фазі. Запаси відображені на малюнку 5.13.

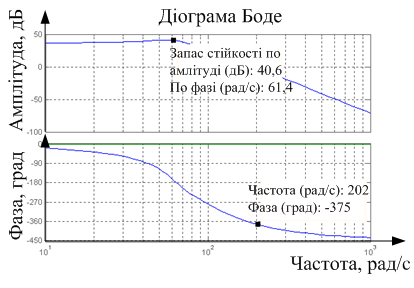
Малюнок 5.13 – ЛАЧХ і ЛФЧХ розімкненої скоректованої системи

Запас стійкості по амплітуді рівний 40.6 дБ, по фазі -375 град. Зв'язана частота ω_З=202 рад/с. Запас стійкості системи достатні, щоб система залишалася стійкою при варіаціях параметрів, приводу і інших функціональних пристроїв в допустимих межах.

Побудуємо годограф Найквіста незмінної частини досліджуваної системи сервоприводу з урахуванням нелінійності в середовищі MATLAB. Результат обчислення АФЧХ приведений на малюнку 5.14.

Аналіз годографа частотної характеристики незмінної частини системи показує, що годограф перетинає речовинну вісь в крапці (60; jO). Виходячи з критерію стійкості Найквіста, можемо укласти, що замкнута досліджувана система буде стійкою, якщо точка перетину годографом речовинної осі буде ліво крапки (-1; j0), тобто коли.

На даному етапі проектування виконується перевірка відповідності показників якості управління скоректованої, досліджуваної системи сервоприводу з урахуванням нелінійності по вимогах технічного завдання (ТЗ). Якщо всі показники якості скоректованої системи задовольняють вимогам ТЗ, то знайдений алгоритм роботи системи приймається до реалізації. Якщо якийсь із показників якості управління скоректованої системи не відповідає вимогам ТЗ, то необхідно повернутися до етапу синтезу алгоритму управління і відповідним чином змінити форму бажаної ЛАЧХ розімкненої системи [13].

Оцінка якості проводиться по перехідних характеристиках замкнутої системи і по частотних характеристиках розімкненої і замкнутої системи.

Сталі помилки оцінюємо по перехідних характеристиках при t >∞. З малюнка 5.15 виходить, що ε_стале=0%.

Сталу швидкісну помилку оцінюємо по реалізації скоректованої системи на швидкісне задаюче дію при t >∞. З малюнка 5.15 виходить, що ε_шв ≈ 0,93%.