Дослідницька частина

5. Дослідницька частина

5.1 Вибір кругового коефіцієнту нелінійного сервоприводу

В нелінійних системах звичайно присутні автоколивання. Як основний критерій при виборі кругового коефіцієнта використовують вимоги відсутності автоколивань в нелінійній системі. Щоб досліджувати систему на автоколивання, треба її розімкнути так, щоб виділити нелінійність.

Всю розімкнену систему замінюємо двома ланками: лінійної і нелінійної частинами (мал. 5.2)

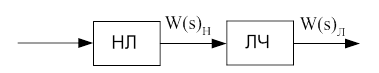
Малюнок 5.2 – Ланки: лінійна і нелінійна частина

Використовують метод гармонійної лінеаризації. Запишемо умову наявності автоколивань в системі: , звідси 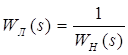 (умова наявності автоколивань в системі).

Перейдемо до умови відсутності автоколивань. Ця умова запишеться , отже 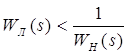 – умова відсутності автоколивань. Це означає, що годограф W_Л(s) і годограф  не перетинаються, тоді, автоколивання в системі відсутні. Вигляд  різний, залежно від того, яка нелінійність переважає. Якщо немає петлі, то нелінійність однозначна (мал. 5.3).

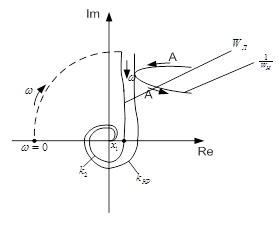
Малюнок 5.3 – Годограф без петлі

Те мінімальне значення кругового коефіцієнта посилення сервоприводу, при якому виконується умова існування автоколивань в системі, назвемо критичним.

Чому мінімальне?

Перетин годографів може бути найрізноманітнішим. Завжди в системі буде два граничні цикли. Один стійкий, інший нестійкий. Але коефіцієнт не буде критичним.

Найменший коефіцієнт, який виходить тільки при торканні і буде мінімальним і критичним. Оскільки, якщо його зменшити, то будуть відсутні автоколивання.

Розглянемо деякий окремий випадок.

Розмикаємо систему на вході нелінійної ланки (мал. 5.4)

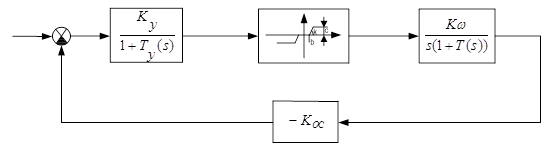
Малюнок 5.4 – Розімкнена система на вході нелінійної ланки

де .

Передавальна функція лінійної частини системи:

(5.1)

передавальна функція нелінійної частини системи W_Н – це коефіцієнт гармонійної лінеаризації в методі гармонійної лінеаризації. В загальному випадку W_Н складається з речовинної і уявної комплексної складових.

В даному випадку W_Н(s) – це дійсне число.

В загальному випадку: .

В даному випадку: ; .

Для K=1, W_Н(s) виглядає таким чином (малюнок 5.5)

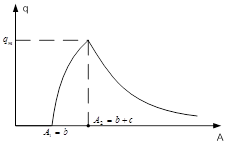
Малюнок 5.5 – Дійсне число WН для K=1

Величина q для однозначної нелінійності залежить тільки від амплітуди А.

Оскільки K=1, то нелінійність виглядає таким чином (малюнок 5.6)

Поки амплітуда А не перевищує зону нечутливості b, тобто до А=b, система розімкнена і A=0.

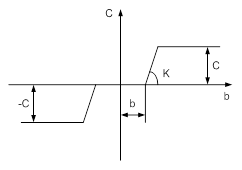
Малюнок 5.6 – Нелінійність для K=1

Побудуємо годограф для W_Л(s) і 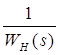(малюнок 5.7)

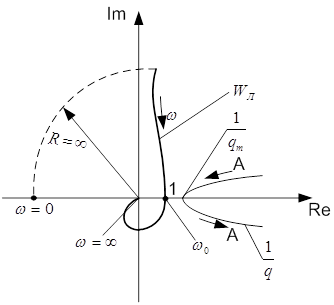
Малюнок 5.7 – Годограф для W_Л(s) і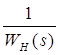

де .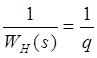

Розглянемо передавальну функцію лінійної частини системи для будь-якої лінійної передавальної функції можна записати:

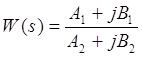(5.2)

Такий запис справедливий, якщо передавальна функція не має нульових полюсів.

А і В-це поліноми від ω.

А – парний ступінь ω; В-непарний ступінь ω.

Крапка 1 на годографі характерна тим, що фазовий зсув чисельника рівний фазовому зсуву знаменника передавальної функції.

Сумарна ФЧХ такої ланки рівна фазовій характеристиці чисельника мінус фазова характеристика знаменника; значить фазовий зсув рівний нулю: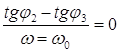, звідс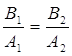и  при . Визначимо модуль передавальної функції лінійної частини системи.

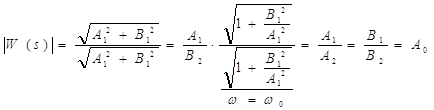
А₀ – модуль передавальної функції на частоті :.

Знайдемо значення частоти .

;

;

;

; .

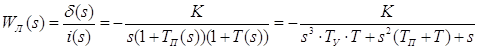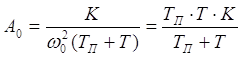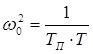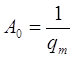З одержаних співвідношень визначаємо значення кругового коефіцієнта нелінійного сервоприводу.

;.

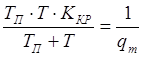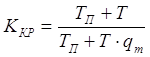Систему більш високого порядку можна апроксимувати системою більш низького порядку для частот в околиці .