Датчик зворотного зв'язку

2.2.3 Датчик зворотного зв'язку

Звичайно як датчик зворотного зв'язку застосовуються, або індукційних датчики (ІД) або потенціометричні. Якщо датчик ЗЗ потенціометр, то в ЗЗ стоїть тільки масштабний опір. Від нього сигнал ЗЗ подається на суматор ПСП. Якщо датчик індукційний, то необхідно мати фазочутливий випрямляч (ФЧВ), а далі знову ставиться масштабний опір.

Перший датчик простіше, легко, але має два експлуатаційні недоліки:

– ковзаючий контакт

– східчаста характеристики

що обмежує його вживання.

Індукційний датчик більш надійних, а отже не вимагає частих перевірок.

Передавальна функція ланцюга зворотного зв'язку має вигляд:

, (2.13)

2.3 Аналіз частотних характеристик досліджуваного об'єкту

Для математичного опису об'єкту управління і системи в цілому спочатку побудуємо структурну схему досліджуваної системи управління сервоприводу без урахування нелінійності (мал. 2.3). Функціональна схема системи управління будувалася на підставі функціональної схеми системи (мал. 1.1).

При виборі параметрів сервоприводу оптимізації підлягає круговий коефіцієнт підсилення (добротність контура сервоприводу):

. (2.14)

Спочатку визначається, а потім з урахуванням відомого коефіцієнта перерозподіляються значення і , щоб виконувалося дана рівність.

Звичайно прагнуть зробити якомога більше, оскільки при цьому зменшуються постійні часу, зменшується запізнювання контура сервоприводу, поліпшується чутливість всіх елементів і розкид параметрів, тобто в цілому поліпшується динаміка сервоприводу. Збільшенню  перешкоджає обмежена потужність, а також те, що при певному значенні  контур стане нестійким.

Запишемо передавальну функцію сервоприводу (СП) в розімкненому стані:

; (2.15)

Ця стійка ланка, оскільки в знаменнику вираз:

дає негативні корені, а корінь s=0 – нульовий полюс, можна обійти справа. Побудуємо АФЧХ.

З амплітудно-фазочастотної характеристики (АФЧХ), яка представлена на малюнку 2.4 видно, що круговий коефіцієнт не може бути як завгодно великим, оскільки при цьому ми одержимо обхват крапки (1, j 0), а значить нестійкість сервоприводу (критерій Найквіста).

При проходженні характеристики через крапку (1, j0) набудемо критичне значення кругового коефіцієнта. Таким чином, при K>K_КР обхвату цієї крапки не буде (система стійка).

При оптимізації кругового коефіцієнта необхідно, щоб розкиди параметрів не привели до нестійкості системи. Звичайно розкиди параметрів повинні мати нульове математичне очікування (М) і підлеглі нормальному закону розподілу. Розкиди кругового коефіцієнта визначаються розкидами кожного з коефіцієнтів: . Якщо ці розкиди некорельовані, мають М=0 і підлеглі нормальному закону розподілу, то достатньо знайти розкиди кругового коефіцієнта. Ми вважатимемо, що коефіцієнти мають випадкові значення.

 – математичні очікування (номінальні значення). В технічних умовах на елементи указуються розкиди на . Кожне із значень не перевищує 3_σ з вірогідністю ≈ 0,997. Трудомісткості полягають в тому, що розкиди звичайно в% від номінальних значеннях, але це можна перевести в одиниці вимірювання, наприклад: задано ∆R – відхилення (розкид) якого-небудь параметра.

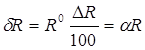(2.16)

де  – середньоквадратичне відхилення.

З теорії вірогідності дисперсія кругового коефіцієнта визначиться як:

(2.17)

По цій формулі можна визначити σ_K в%, а потім перевести в одиниці вимірювання самого параметра.

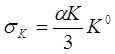(2.18)

де 3σ_К=∆K.

Тут одне невідоме – K, яке визначаємо, знаючи σ_К і K_КР. Крім того повинні бути задані вимоги до запасу стійкості замкнутого контура.

Використовуючи ці положення, можна обчислити круговий коефіцієнт.

2.3.1 Вибір кругового коефіцієнта

Задано:

1) критичне значення кругового коефіцієнта – K_КР (його завжди можна визначити, побудувавши годограф);

2) розкиди  (з технічних умов);

3) вірогідність стійкої роботи сервоприводу – P_СП.

Визначити: номінальне значення кругового коефіцієнта (добротність) – K⁰

1.   Визначаємо ∆K.

 [%],

2.   Розкид параметрів визначає

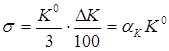
3.   Значення P_СП (Ф(і)) в таблицях інтеграла вірогідності відповідає відносна величина U (або n), рівна:.

В нашому випадку x – це круговий коефіцієнт K, виступаючий як випадкова величина.

Величина U показує, скільки разів вміщається σ в ∆K.

Таблиця інтеграла вірогідності має вигляд: див. табл. 2 в додатку Б.

4.   З графіка інтеграла вірогідності, малюнок 2.5 маємо:

,

де .

Тому  або 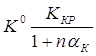 – вираз для визначення номінального значення кругового коефіцієнта сервоприводу.