Статистичні розподіли та чисельні характеристики вибірки

3. Статистичні розподіли та чисельні характеристики вибірки

Значення чисельної ознаки, які спостерігаються в деякій конкретній вибірці, називають варіантами. Послідовність таких варіант у зростаючому порядку – варіаційним рядом. Якщо у вибірці об’єму n варіанта  зустрічається  разів, то число

(3.1)

називають відносною частотою варіанти, а  – частотою варіанти.

Від вибірки до вибірки об’єму n частоти  та відносні частоти  змінюються. Це означає, вони є значеннями випадкових величин  та , відповідно. В подальшому все що стосується конкретної вибірки буде позначатися малими буквами латинського та грецького алфавітів, а все що стосується вибірки взагалі – відповідними великими буквами.

Перелік варіант та відповідних до них частот (або відносних частот) називають статистичним розподілом вибірки. Статистичний розподіл, як правило, задається у вигляді таблиці. Ломана крива, яка з’єднує точки з координатами (x_i, n_i), або (x_i, w_i) у прямокутній системі координат називається полігоном частот.

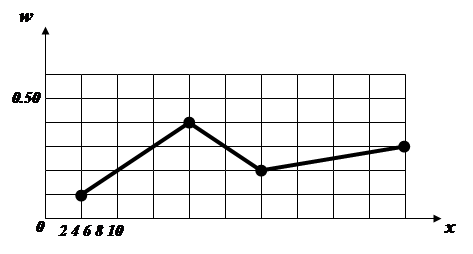
Приклад 3.1. Для конкретної вибірки одержали статистичний розподіл відносних частот

.

Його гістограма має вигляд

Статистичний розподіл вибірки можна також представити у вигляді послідовності інтервалів та відповідних до них частот, що особливо зручно, коли ознакою є неперервна величина. Інтервал з варіантами розбивають на декілька часткових інтервалів довжиною  і знаходять для кожного з них суму частот варіант, які потрапили в інтервал. Якщо всі інтервали рівні (), то відповідні варіанти називають рівновіддаленими, а їх чисельні значення визначаються серединами відрізків. Якщо частота первинної варіанти знаходиться на границі двох інтервалів, то її частота рівномірно розподіляється між ними. Графічно статистичний розподіл з послідовністю інтервалів задається гістограмою частот (відноснихчастот). Для побудови гістограми частот (або відносних частот), необхідно на вісі абсцис відкласти часткові інтервали і побудувати на них як основах прямокутники висотою  . Величини  називають густиною частоти, а величини - густиною відносної частоти. Загальна площа гістограми дорівнює сумі всіх частот, тобто об’єму вибірки n, а площа гістограми відносних частот дорівнює одиниці.

Приклад 3.2. Для конкретної вибірки об'єму одержали розподіл частот по частковим інтервалам

Частковий інтервал довжиною	Сума частот варіант часткового інтервалу	Густина частоти
5-10 10-15 15-20 20-25 25-30 30-35 35-40	4 6 16 36 24 10 4	0.8 1.2 3.2 7.2 4.8 2.0 0.8

Полігон частот такого розподілу має такий вигляд

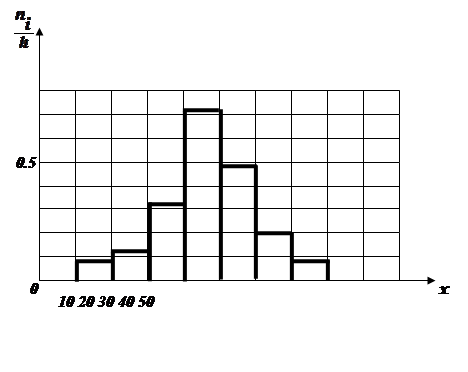
Емпіричною інтегральною функцією вибірки називають функцію

,(3.2)

 – кількість варіант менших ніж x (дискретна випадкова аеличина).

На відміну від емпіричної інтегральної функції розподілу вибірки, інтегральну функцію розподілу генеральної сукупності називають теоретичною інтегральною функцією розподілу. З теореми Бернуллі слідує, що відносна частота події  тобто  по ймовірності прямує до ймовірності  цієї події. Це означає, що емпірична функція вибірки по ймовірності прямує до теоретичної функції розподілу генеральної сукупності. Тому емпірична функція розподілу вибірки є оцінкою теоретичної функції генеральної сукупності.

Із означення емпіричної функції слідують такі її властивості: