Навигация
Стандартні розподіли математичної статистики
31115
знаков
4
таблицы
3
изображения
4. Стандартні розподіли математичної статистики
4.1 Розподіл 
(хі-квадрат)
Нехай 
- система нормальних випадкових величин з одинаковими математичними сподіваннями 
та середньоквадратичними відхиленнями 
. Тоді сума квадратів цих величин 
розподілена за законом 
(хі квадрат) із 
степенями свободи. Густина розподілу
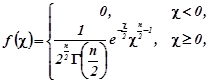(4.1.1)
де 
- гамма-функція (додаток 1.11).
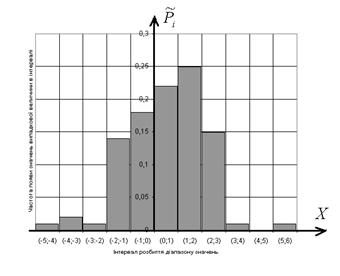
Розподіл однозначно визначається одним параметром – числом степені свободи n. Із збільшенням числа степеней свободи розподіл повільно наближається до нормального (додаток 1.12).
Математичне сподівання та дисперсія розподілу
,
.
Доведення. За означенням математичного сподівання
,
,
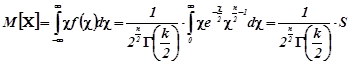(використана рівність 
).
З врахуванням цього
.
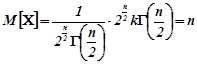Для обчислення дисперсії зручно скористатися формулою
.
За означенням математичного сподівання
,
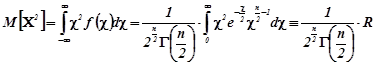З врахуванням цього
.
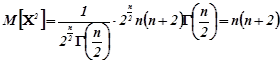
4.2 Розподіл Стьюдента
Якщо Z – нормальна випадкова величина з параметрами 
та 
, а V – незалежна від Z величина, розподілена за законом із n степенями свободи, то випадкова величина
має розподіл, який називають розподілом Стьюдента, з густиною
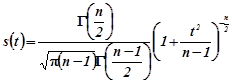.(4.2.1)
Розподіл Стьюдента однозначно визначається одним параметром – числом степеней свободи розподілу випадкової величини V (додаток 1.13)
Функція 
симетрична, тому математичне сподівання розподілу Стьюдента дорівнює нулю:
,(4.2.2)
а дисперсія
.(4.2.3)
4.3 Розподіл F Фішера-Снедекора
Якщо U і V – незалежні випадкові величини розподілені за законом з 
степенями свободи, відповідно, то випадкова величина
(4.3.1)
має розподіл , який називається розподілом F Фішера-Снедекора з густиною
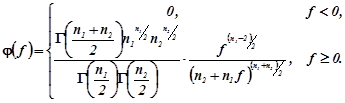(4.3.2)
Розподіл F Фішера-Снедекора однозначно визначається двома параметрами (додаток 1.14).
Математичне сподівання та дисперсія випадкової величини 
відповідно дорівнюють
,(4.3.3)
.(4.3.4)
Розподіл F Фішера-Снедекора називають ще 
-розподілом.
Похожие работы
... ія розподілення експоненціального закону: , а імовірність попадання у інтервал (a,b) безперервної випадкової величини Х, розподіленою за експоненціальним законом дорівнює: . 2. Види типових задач з математичної статистики Тип 1 Ланка дослідів дала певну послідовність результатів. Вирахувати середнє значення виміряння, дисперсію, похибки, а також встановити закони розподілення ...
... необхідності допускається застосування байєсівських процедур. Байєсівський підхід стає все більш популярним в області фармакокінетики. Можна сказати, що клінічні дослідження мають ще тривалішу історію, ніж математична статистика. Клінічні дослідження в тому розумінні, що ми звикли вкладати в це поняття, в основному одержали розвиток після другої світової війни, хоча відомі і більш ранні приклади. ...
... ідому р і. Знайти функцію розподілу випадкової величини F(Х) та побудувати її графік. Обчислити математичне сподівання М(Х), дисперсію D(Х) та середнє квадратичне відхилення випадкової величини Х. Х 11 13 15 19 Р 0,18 0,32 0,4 ? Розв’язання Згідно з умовою нормування розподілу ймовірностей випадкової величини Звідси знаходимо : Функцію розподілу знаходимо на основі ...
... яким чином досягти певного рівня обслуговування (максимального скорочення черги або втрат вимог) при мінімальних витратах, пов'язаних з простоєм обслуговуючих устроїв. математичне моделювання економічний аналіз 2. Прийоми економічного аналізу на базі математичної статистики Застосування методів моделювання в аналітичному дослідженні господарської діяльності підприємств та їхніх структурних ...
0 комментариев