Навигация
Метод максимальної правдоподібності
7. Метод максимальної правдоподібності
Метод максимальної провдоподібності використовуються для знаходження статистичних оцінок параметрів розподілів випадкових величин (як дискретних, розподіл яких задається аналітичним виразом, так і неперервних випадкових величин).
Нехай X – випадкова величина з розподілом (якщо вона дискретна) або густиною розподілу ймовірностей (якщо вона неперервна) ![]() , який (яка) однозначно визначається параметром
, який (яка) однозначно визначається параметром![]() , і який невідомий. Для його визначення здійснюється n експериментів. Результати кожного з експериментів є випадковими величинами
, і який невідомий. Для його визначення здійснюється n експериментів. Результати кожного з експериментів є випадковими величинами ![]() . Очевидно, що розподіли цих випадкових величин співпадають з функцією
. Очевидно, що розподіли цих випадкових величин співпадають з функцією ![]() випадкової величини X. Експерименти незалежні, тому за теоремою множення ймовірностей незалежних подій можна записати
випадкової величини X. Експерименти незалежні, тому за теоремою множення ймовірностей незалежних подій можна записати
![]() .
.
Функція
![]() (2.1)
(2.1)
називається функцією максимальної правдоподібності. Точка ![]() , в якій функція максимальної правдоподібності досягає максимуму є значенням статистичної оцінки
, в якій функція максимальної правдоподібності досягає максимуму є значенням статистичної оцінки ![]() параметра розподілу
параметра розподілу ![]() . Така статистична оцінка називається оцінкою найбільшої правдоподібності.
. Така статистична оцінка називається оцінкою найбільшої правдоподібності.
Функції ![]() та
та ![]() досягають максимуму в одинакових точках. Тому замість точки максимуму функції
досягають максимуму в одинакових точках. Тому замість точки максимуму функції ![]() шукають точку максимуму функції
шукають точку максимуму функції ![]() , що значно зручніше. З математичного аналізу відомо, що точку максимума функції можна знайти за таким алгоритмом:
, що значно зручніше. З математичного аналізу відомо, що точку максимума функції можна знайти за таким алгоритмом:
1) знаходять похідну і прирівнюють до нуля: ![]() ;
;
2) розв’язують одержане рівняння і знаходять екстремальні точки ![]() ;
;
3) знаходять другу похідну ![]() ; якщо друга похідна в екстремальній точці від’ємна, то така точка є точкою максимума функції, якщо додатня, то – мінімуму.
; якщо друга похідна в екстремальній точці від’ємна, то така точка є точкою максимума функції, якщо додатня, то – мінімуму.
Методом максимальної правподібності одержані важливі для практики результати:
1) статистична оцінка параметра ![]() розподілу Пуассона
розподілу Пуассона
![]() ;(2.2)
;(2.2)
2) статистична оцінка параметра p біноміального розподілу є
![]() ,(2.3)
,(2.3)
n1 кількість експериментів у першій серії, X1 - кількість успіхів; : n2 кількість експериментів у другій серії, X2 - кількість успіхіву другій серії;
3) статистичною оцінкою параметра ![]() експоненціального розподілу є обернена величина до вибіркового середнього:
експоненціального розподілу є обернена величина до вибіркового середнього:
![]() .(2.4)
.(2.4)
Якщо розподіл випадкової величини однозначно визначається не одним параметром, а декількома, то функція максимальної правподобності є функцією багатьох змінних:
![]() .
.
В цьому випадку для знаходження точок максимуму необхідно розв’язати систему нелінійних рівнянь
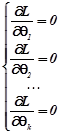 (2.5)
(2.5)
Саме цим користуються для знаходження статистичних оцінок параметрів нормального розподіл у теорії похибок вимірювання фізичних величин.
8. Теорія похибок вимірювання фізичних величин
Кількісні результати при спостереженнях одержують, як правило, шляхом вимірювання. Якщо істинне значення деякої фізичної величини a, а в результаті вимірювання одержане значення x, то похибка вимірювання визначається як різниця між ними: ![]() . Розрізняють три види похибок: промахи, систематичні похибки та випадкові похибки.
. Розрізняють три види похибок: промахи, систематичні похибки та випадкові похибки.
Промахи виникають через грубе порушення умов вимірювання (неправильні дії лаборанта, несправність вимірювальної аппаратури, різка зміна зовнішніх умов) і зазвичай характеризуються порівняно великими похибками.
Систематичні похибки є результатом впливу не врахованих факторів (підвищена температура, електромагнітні завади, тощо) або недоліками вимірювальних приладів (похибка градуювання, недосконалість методу вимірювання) Промахи та систематичні похибки можуть бути виявлені і враховані як при обробці вимірювань, так і при організації вимірювань. Але як би не були добре організовані вимірювання, завжди залишається багато не врахованих факторів, вплив яких приводить до випадкових похибок.
Похожие работы
... ія розподілення експоненціального закону: , а імовірність попадання у інтервал (a,b) безперервної випадкової величини Х, розподіленою за експоненціальним законом дорівнює: . 2. Види типових задач з математичної статистики Тип 1 Ланка дослідів дала певну послідовність результатів. Вирахувати середнє значення виміряння, дисперсію, похибки, а також встановити закони розподілення ...
... необхідності допускається застосування байєсівських процедур. Байєсівський підхід стає все більш популярним в області фармакокінетики. Можна сказати, що клінічні дослідження мають ще тривалішу історію, ніж математична статистика. Клінічні дослідження в тому розумінні, що ми звикли вкладати в це поняття, в основному одержали розвиток після другої світової війни, хоча відомі і більш ранні приклади. ...
... ідому р і. Знайти функцію розподілу випадкової величини F(Х) та побудувати її графік. Обчислити математичне сподівання М(Х), дисперсію D(Х) та середнє квадратичне відхилення випадкової величини Х. Х 11 13 15 19 Р 0,18 0,32 0,4 ? Розв’язання Згідно з умовою нормування розподілу ймовірностей випадкової величини Звідси знаходимо : Функцію розподілу знаходимо на основі ...
... яким чином досягти певного рівня обслуговування (максимального скорочення черги або втрат вимог) при мінімальних витратах, пов'язаних з простоєм обслуговуючих устроїв. математичне моделювання економічний аналіз 2. Прийоми економічного аналізу на базі математичної статистики Застосування методів моделювання в аналітичному дослідженні господарської діяльності підприємств та їхніх структурних ...
0 комментариев