Навигация
Порядок обробки вимірювань
8.3 Порядок обробки вимірювань
У теорії похибок вибіркове середнє ![]() позначають як
позначають як ![]() ; її точність
; її точність ![]() при відомому
при відомому ![]() - як
- як ![]() , де
, де
![]() - середня похибка;(6.3.1)
- середня похибка;(6.3.1)
її точність по Стьюденту ![]() - як
- як ![]() .
.
При обчисленні ![]() та s зручно користуватися формулами
та s зручно користуватися формулами
![]() ;(6.3.2)
;(6.3.2)
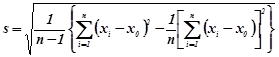 (6.3.3)
(6.3.3)
де ![]() – довільна стала (умовний нуль), яку вибирають заокругленним числом, близьким до
– довільна стала (умовний нуль), яку вибирають заокругленним числом, близьким до ![]() .
.
Остаточний результат вимірювання прийнято записувати у вигляді ![]() . У класичній теорії похибок це означає, що істинне значення фізичної величини покривається довірчим інтервалом
. У класичній теорії похибок це означає, що істинне значення фізичної величини покривається довірчим інтервалом ![]() з надійністю
з надійністю ![]() (
(![]() - функція ймовірності). У статистиці малих вибірок (мікростатистиці) це означає, що істинне значення фізичної величини покривається довірчим інтервалом
- функція ймовірності). У статистиці малих вибірок (мікростатистиці) це означає, що істинне значення фізичної величини покривається довірчим інтервалом ![]() з надійністю (ймовірністю)
з надійністю (ймовірністю) ![]() - (
- (![]() значення густини розподілу Стьюдента у точці
значення густини розподілу Стьюдента у точці ![]() ). При великій кількості вимірювань (
). При великій кількості вимірювань (![]() ) надійності довірчих інтервалів класичної теорії похибок та мікростатистики практично співпадають.
) надійності довірчих інтервалів класичної теорії похибок та мікростатистики практично співпадають.
Приклад 6.3.1.Приклад обробки рівноточних вимірювань, результати яких наведені у наступній таблиці:
| i |
|
|
|
| 1 2 3 4 5 6 7 8 9 10 11 12 | 18338 18316 18325 18341 18332 18319 18313 18329 18310 18322 18330 18314 | 18 -4 5 21 12 -1 -7 9 -10 2 10 -6 | 324 16 25 441 144 1 49 81 100 4 100 36 |
|
|
| 49 | 1321 |
![]()
За формулами (3.2), (3.3), (3.1)
![]() ,
, 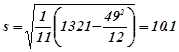 ,
, ![]()
Остаточно
![]() .
.
У класичній теорії похибок це означає, що істинне значення фізичної величини покривається інтервалом ![]() з надійністю
з надійністю ![]() . У мікростатистиці надійність цього довірчого інтервалу менша:
. У мікростатистиці надійність цього довірчого інтервалу менша:![]() (при
(при ![]() ). Із збільшенням довірчого інтервалу його надійність збільшується:
). Із збільшенням довірчого інтервалу його надійність збільшується:
надійність довірчого інтервалу
![]()
дорівнює ![]() у класичній теорії похибок і
у класичній теорії похибок і ![]() у мікростатистиці.
у мікростатистиці.
Якщо вимірювання фізичної величини відбувається при різних умовах, з використанням різних методик та обладнання, то говорять про нерівноточні вимірювання. При обробці нерівноочних вимірювань, кожному вимірюванню приписується певна вага, яка , як правило, задається цілими числами.Найменш надійному вимірювання приписують найменшу вагу (наприклад, ![]() ), а решту вимірюванням приписуть вагу тим більшу, чим надійніші вимірювання.
), а решту вимірюванням приписуть вагу тим більшу, чим надійніші вимірювання.
Зручно розглядати вагу вимірювання як повторювання вимірювання, тобто вважати, що одне вимірювання з вагою ![]() рівноцінне
рівноцінне ![]() вимірювань з одиничною вагою, що сприяє зменшенню середньої похибки у
вимірювань з одиничною вагою, що сприяє зменшенню середньої похибки у ![]() разів (6.3.1). Обробка нерівноточних вимірювань здійснюється аналогічно до рівноточних з тією лише різницею, що формули для
разів (6.3.1). Обробка нерівноточних вимірювань здійснюється аналогічно до рівноточних з тією лише різницею, що формули для ![]() мають вигляд:
мають вигляд:
![]() ;(6.3.4)
;(6.3.4)
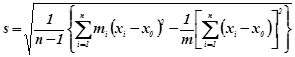 (6.3.5)
(6.3.5)
![]() (6.3.6)
(6.3.6)
де ![]() (n – кількість нерівноточних вимірювань).
(n – кількість нерівноточних вимірювань).
Приклад 6.3.2.Приклад обробки нерівноточних вимірювань, результати яких наведені у наступній таблиці:
| i |
|
|
|
|
|
| 1 2 3 4 5 6 7 8 | 236.4 241.6 242.0 240.7 237.4 239.5 243.8 242.5
| 1 3 1 5 3 5 3 5 | -3.6 1.6 2.0 0.7 -2.6 -0.5 3.8 2.5 | -3.6 4.8 2.0 3.5 -7.8 -2.5 11.4 12.5 | 12.96 7.68 4.00 2.45 20.28 1.25 43.32 31.25 |
|
|
| 26 |
| 20.3 | 123.19 |
![]() .
.
За формулами (3.4), (3.5), (3.4)
![]() ;
; ![]() ;
; ![]() .
.
Отже, у підсумку ![]()
Похожие работы
... ія розподілення експоненціального закону: , а імовірність попадання у інтервал (a,b) безперервної випадкової величини Х, розподіленою за експоненціальним законом дорівнює: . 2. Види типових задач з математичної статистики Тип 1 Ланка дослідів дала певну послідовність результатів. Вирахувати середнє значення виміряння, дисперсію, похибки, а також встановити закони розподілення ...
... необхідності допускається застосування байєсівських процедур. Байєсівський підхід стає все більш популярним в області фармакокінетики. Можна сказати, що клінічні дослідження мають ще тривалішу історію, ніж математична статистика. Клінічні дослідження в тому розумінні, що ми звикли вкладати в це поняття, в основному одержали розвиток після другої світової війни, хоча відомі і більш ранні приклади. ...
... ідому р і. Знайти функцію розподілу випадкової величини F(Х) та побудувати її графік. Обчислити математичне сподівання М(Х), дисперсію D(Х) та середнє квадратичне відхилення випадкової величини Х. Х 11 13 15 19 Р 0,18 0,32 0,4 ? Розв’язання Згідно з умовою нормування розподілу ймовірностей випадкової величини Звідси знаходимо : Функцію розподілу знаходимо на основі ...
... яким чином досягти певного рівня обслуговування (максимального скорочення черги або втрат вимог) при мінімальних витратах, пов'язаних з простоєм обслуговуючих устроїв. математичне моделювання економічний аналіз 2. Прийоми економічного аналізу на базі математичної статистики Застосування методів моделювання в аналітичному дослідженні господарської діяльності підприємств та їхніх структурних ...
0 комментариев