Навигация
Цилиндрические зубчатые передачи
5. Цилиндрические зубчатые передачи
5.1 Силы в зацеплении
Силы принято определять в полюсе W (рис.5) зацепления.
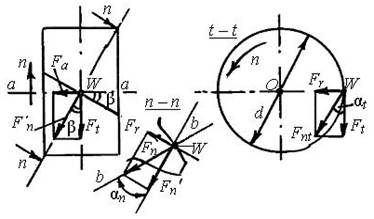
Рис.5
По линии зацепления b – b (рис. 5) действует нормальная сила Fn. Для удобства расчетов силу Fn принято раскладывать на три составляющие:
1) Ft – окружная сила, направленная по касательной к делительным окружностям. Это основная, движущая, полезная сила. На колесе z2 Ft совпадает с направлением вращения n2. На шестерне z1 F направлена против вращения n1.
Следовательно, на рис. 5 дана схема сил для шестерни:
Ft = 2000Т / d, (1)
где Т – Н∙м; d – мм;
2) Fr – радиальная сила, направленная по линии центров (радиусам). Для внешнего зацепления – к оси вращения, для внутреннего – от оси.
В торцовой плоскости t – t (рис. 5) имеем
Fr = tgαt, (2)
где αt – делительный угол профиля в торцовой плоскости: tgαt = tgαn / cosβ; αn– нормальный угол зацепления, β – угол наклона зубьев. В практических расче-тах αt ≈ αn =20°.
3) Fa – осевая сила, направленная параллельно оси а – а зубчатого коле-
са. Силы Ft и Fа как составляющие нормальной силы Fn′, всегда находятся вне линии зуба (рис. 5). В делительной плоскости:
Fа = Fttgβ. (3)
Необходимый в дальнейших расчетах основной угол наклона зуба
βb (в основной плоскости зацепления b) определяется как βb = arcsin(sinβcosαn).
Полная нормальная сила (рис. 5):
Fn = Fnt / cosβb = Ft / (cosαtcosβb). (4)
Для прямозубых передач во всех формулах β = βb = 0; αt = αn = α;
Ft = 2000T / d; Fr = Fttgα; Fa = 0; Fn = Ft / cosα.
Недостатком косозубых передач является наличие осевых сил Fа, которые дополнительно нагружают опоры валов, усложняя их конструкцию.
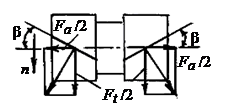
Рис. 6
В косозубых передачах углы β ограничены в пределах 8…18°.
Указанный недостаток устранен в шевронной передаче, которая представляет собой сдвоенную косозубую с противоположным наклоном зубьев на полушевронах. Из рис. 6 видно, что осевые силы Fа /2 взаимоуравновешены.
5.2. Расчет на сопротивление контактной усталости
Косые зубья цилиндрических колес нарезают тем же инструментом, что и прямые, установленным относительно заготовки под углом β.
Расчет на прочность принято вести для прямозубой передачи. Для этого все зубчатые и червячные передачи приводятся к эквивалентным прямозубым цилиндрическим.
Эквивалентные параметры косозубого цилиндрического колеса (приведение рассматривалось в курсе "Теория машин и механизмов"): делительный диаметр dv = d / cos2β; эквивалентное число зубьев zv = z / cosβ, где z – действительное число зубьев косозубого колеса.
С увеличением β эквивалентные параметры возрастают, способствуя повышению прочности передачи. Вследствие того, что косой зуб входит в зацепление не сразу всей длиной, он лучше прирабатывается, а большее число пар зубьев в зацеплении снижает шум и динамические нагрузки. Чем больше угол β, тем выше плавность зацепления.
Контактная прочность (σН ≤ σНР) является основным критерием работоспособности большинства зубчатых передач.
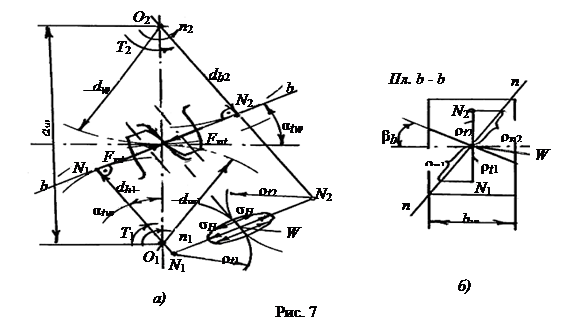
Расчет производят в полюсе W (рис. 7), где имеет место наибольшая нагрузка (зона однопарного зацепления) и начинается усталостное выкрашивание зубьев.
Контакт зубьев рассматривают как сжатие двух цилиндров в плоскостях n и b
Контакт зубьев рассматривают как сжатие двух цилиндров в плоскостях n с нормальными радиусами кривизны ρn1 и ρn2. Используют формулу Герца для первоначального контакта по линии:
σН = ZE(wHn / ρnv)1/2 ≤ σНP. (5)
Напряжения σН одинаковы для зубьев z1 и z2. Оценку сопротивления контактной усталости производят по расчетной величине допускаемого напряжения σНР.
В формуле (5): ZE = (1 / {π[(1 – ν12) / E1 + (1 – ν22) / E2]})1/2 –
– коэффициент механических свойств материалов z1 и z2: Е – модуль упругости; ν1, 2 – коэффициенты Пуассона. Для стали Е1 = Е2 = 2,1∙105 МПа, ν1 = ν2 = 0,3 и ZЕ =191,6 МПа1/2;
wHn = FnKH / lΣ – удельная нормальная расчетная нагрузка (на единицу длины lΣ контактных линий), Н/мм, где KH – коэффициент нагрузки; Fn – нормальная сила.
Вспомним, что lΣ = bwεα / cosβb, где εα – торцовый коэффициент перекрытия; Fn = Ft / (cosαtcosβb). Тогда получим wHn = FtKH / (bwεαcosα
1 / ρnv = 1 / ρn1 ± 1 / ρn2 – приведенная кривизна зубьев в нормальной плоскости, 1/мм.
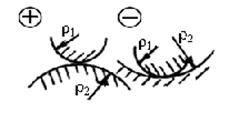
Рис. 8
Знак плюс принимают при контакте двух выпуклых тел (рис. 8), минус – выпукло (ρ1)-вогнутых (ρ2) тел (например, внутреннее зацепление).
| Нормальные радиусы кривизны (рис. 7, б) ρn = ρt / cosβb, где из ΔONW (рис. 7, а) торцовый радиус ρt = dwsin αtw / 2. |
Выразив 1 / ρnv через параметры передачи,
получим  , где d1 – делительный диаметр шестерни z1.
, где d1 – делительный диаметр шестерни z1.
Подставив wHn и 1 / ρnv в формулу (5) и обозначив Zε = ![]() – коэффициент, учитывающий суммарную длину контактных линий (для прямых зубьев Zε =
– коэффициент, учитывающий суммарную длину контактных линий (для прямых зубьев Zε = ![]() );
);
ZH = 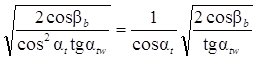 – коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе W, получим решение в форме ГОСТ 21354-87:
– коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе W, получим решение в форме ГОСТ 21354-87:
σН = ZEZεZH , (6)
, (6)
где знак плюс – для внешнего зацепления; минус – для внутреннего.
Это формула для проверочного расчета активных поверхностей зубьев цилиндрических передач на сопротивление контактной усталости с целью предотвращения поверхностного выкрашивания.
В проектировочном расчете из условия контактной прочности определяют межосевое расстояние аw – основной габаритный размер передачи.
Для этого в формуле (6) принимают ZE = 191,6 МПа1/2, в среднем εα =
= 1,6 и Zε = 0,8 – косые и шевронные зубья (β ≠ 0), Zε = 0,9 – прямые зубья (β = 0); αt = αtw = αn = 20°, ZН = 2,5 – прямые зубья, ZН = 2,46 – косые (β = 10О) зубья. Вводят коэффициент рабочей ширины ψba зубчатого венца по межосевому расстоянию: ψba = bw / аw , заменяя bw = ψbaаw. Диаметр d1 = 2аw / (u ± 1). Окружная сила Ft = 2000T1 / d1. Тогда будем иметь
аw′ = Ка(и ± 1) , (7)
, (7)
где Ка = ZEZεZH![]() , при β ≠ 0 Ка = 410 МПа1/3, при β = 0 Ка = 450 МПа1/3.
, при β ≠ 0 Ка = 410 МПа1/3, при β = 0 Ка = 450 МПа1/3.
В формуле (7) аw′, мм, Т1 , Н∙м, σНР , МПа.
Расчетное значение аw′ округляют до аw в ближайшую большую сторону:
– для стандартных передач по ГОСТ 2185-66 (по ряду чисел Ra20);
– для нестандартных передач возможно округление до числа, кратного пяти.
Формула (7) главная для проектировочного расчета закрытых цилиндрических передач с целью предотвращения усталостного выкрашивания поверхностей зубьев.
5.3 Расчет на сопротивление изгибной усталости
1. Прямозубая передача
Приняты следующие допущения:
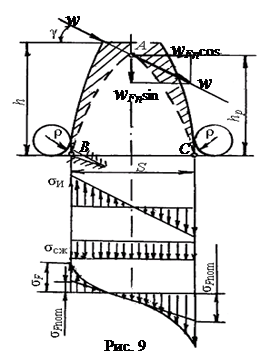
1. Нагрузка передается одной парой зубьев (lΣ = bw) и приложена к вершине зуба по линии зацепления N1N2 под углом γ (γ > αtw) (рис. 9).
2. Зуб рассматривается как вписанная в него консольная балка АВС параболического профиля, имеющая равное сопротивление изгибу в сечениях по высоте hp.
Удельная линейная расчетная нагрузка wFn = Fn / lΣ = FtKF / (bwcosα), где KF – коэффициент нагрузки при расчете на изгиб (KF = KАKFβKFvKFα). Нагрузка FtKF / bw = wFt – удельная окружная и wFn = wFt / cosα. Нагрузка wFn переносится в точку А и раскладывается на составляющие wFncosγ и wFnsinγ.
В заделке ВС балки возникают напряжения изгиба σи = wFncosγ∙hp / W и сжатия σсж = wFnsinγ / A, где W – момент сопротивления изгибу сечения ВС; А – площадь сечения ВС при его ширине, равной единице (bw = 1 мм так как нагрузка wFn единичная) и длине s; W = 1∙s2 / 6 и А = 1∙s.
| Суммарные номинальные напряжения (рис. 9): – в точке В σFnomB = σи – σсж ≤ £ σFР (растяжение); – в точке С σFnomС = σи + σсж ≤ £ σFР (сжатие). Несмотря на то, что максимальные напряжения возникают в точке С – сжатия ножки зуба, усталостные трещины и разрушение зубьев начинаются на растянутой стороне в точке В. Расчет ведут по напряжениям σFnomB растянутой стороны. Расчетное сечение ВС расположено в зоне концентрации напряжений, вызванной изменением формы выкружкой (галтелью) радиуса ρ на переходной поверхности. Это учитывается коэффициентом концентрации напряжений ασ. Местное напряжение изгиба σF = ασσFnomB.. |
|
Раскрывая последнюю формулу в точке В, будем иметь
σF = 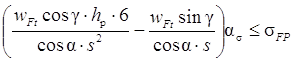 .
.
Исходя из геометрического подобия зубьев разных модулей, плечо hp и толщину s выражают через модуль m: hp = μm, s = λm, где μ и λ – коэффициенты, учитывающие форму зуба.
Тогда σF =  .
.
Введя YFS = 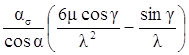 – коэффициент, учитывающий форму зуба и концентрацию напряжений, получим
– коэффициент, учитывающий форму зуба и концентрацию напряжений, получим
σF = wFtYFS / m ≤ σFP. (8)Величины YFS приведены в литературе в виде графиков или таблиц.
Подставляя значение wFt в формулу (8), получим формулу для проверочного расчета прямых зубьев на сопротивление усталости при изгибе:
σF = FtKFYFS / (bwm) ≤ σFP. (9)
2. Косозубая передача
Специфика косозубой передачи определяет следующие дополнительные отличия:
1. Наклон контактных линий к основанию зуба учитывается коэффициентом: Yβ = 1 – εββ0 / 120 ≥ 0,7,
где εβ – коэффициент осевого перекрытия зубьев.
2. Лучшая прирабатываемость и большее перекрытие зубьев – Yε = 1 / εα.
3. Коэффициент YFS определяют в зависимости от эквивалентного числа зубьев zv = z / cos3β.
Расчетная формула (9) для косозубых передач примет вид:
σF = FtKFYFSYβYε / (bwm) ≤ σFP.(10)
Расчет на изгиб ведут по тому зубу, у которого меньше отношение σFР / YFS.
Если известно σF1, то σF2 = σF1YFS2 / YFS1.
Похожие работы
... Направление линии зуба правое. Вращение против часовой стрелки. при bm=35° при bm=35° Направление линии зуба левое. Вращение по часовой стрелке. 7. РАСЧЁТ ЧЕРВЯЧНОЙ ПЕРЕДАЧИ 7.1 Выбор материалов червяка и червячного колеса Для изготовления червяков применяют углеродистые и легированные стали (см. табл. 3.1). Выбор марки стали зависит от назначаемой термообработки ...
... …….…………………………………………………………..7 5. Последовательность проектного расчета закрытых конических прямозубых передач……………………………………………………….20 6. Последовательность проектного расчета червячных передач...……..24 Библиографический список……………………………………………….31 1. Цель и задачи курсового проектирования Курсовое проектирование является заключительным этапом в изучении общеинженерных курсов «Прикладная ...
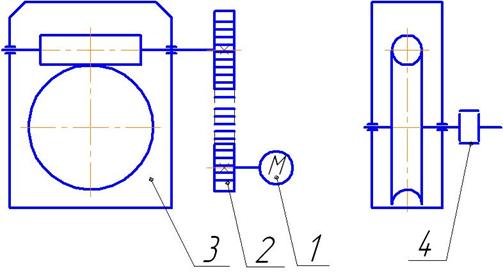
... посадок отдельных деталей. В местах посадки подшипников при вращении внутреннего кольца рекомендуют поля допусков для вала n6, m6, k6. Свободные размеры принимают по 14 квалитету. 3.2 Кинематическая схема мотор-редуктора и силы, действующие в зацеплениях зубчатых колес. Кинематическая схема трехступенчатого мотор - редуктора включает в себя червячную, коническую и цилиндрическую прямозубые ...
... валы червячного редуктора (рис.7): Рис.7 Схема усилий, действующих на валы червячного редуктора Определяем консольную нагрузку на муфте [1,табл.6.2]: ; (10.1) Н Для определения консольной нагрузки на шкиве необходимо произвести расчет зубчато-ременной передачи.[1]. Определяем минимальный диаметр ведущего шкива по диаметру ...

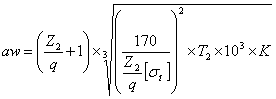
0 комментариев