Навигация
Определение модуля передачи
3. Определение модуля передачи
Модуль m = P / π, где шаг Р = πd / z, введен для того. чтобы избавиться от иррационального числа π (m = d / z).
а) Закрытые передачи
Модуль определяют из условия равнопрочности зубьев по усталостному выкрашиванию и изгибу, т.е. через аw и bw:
m′ ≥ 103∙Т1(и ± 1)KFYFSYβYε / (аwbwσFР). (11)
Модуль m′ округляют по ГОСТ 9563-60 до ближайшего большего значения с предпочтением первого ряда. В силовых передачах mn ≥ 1,5 мм.
б) Открытые и высокотвердые (Н0 ≥ 56 HRC) передачи
Для этих передач изгибная прочность является основным критерием работоспособности. Их проектировочный расчет начинают с определения модуля из условий изгиба:
m′ ≥ Кm [T1KFβYFS1 / (ψbd z12σFP1)]1/3, (12)
где Кm = 12,6 – для прямозубых передач; Кm = 10 – для косозубых передач. Числом зубьев z1 и коэффициентом ψbd следует задаваться.
Модуль m′ округляют по ГОСТ 9563-60. Для силовых передач m ≥ 1,5 мм.
6. Конические зубчатые передачи
6.1. Основные параметры
Конические зубчатые передачи применяют для передачи энергии между пересекающимися осями валов. Наибольшее применение имеют ортогональные передачи с межосевым углом Σ = 90° (рис. 10).
Конические колеса бывают с прямыми (в открытых передачах) и круговыми (в редукторах) зубьями. Круговые зубья очерчены линиями по дугам окружности.
Конуса с вершиной в точке О являются основными (рис.10). Внешние и внутренние торцы на конических зубчатых колесах формируют внешними (вершины Ое) и внутренними (вершины Оi) дополнительными конусами, образующие которых перпендикулярны образующей делительного конуса.
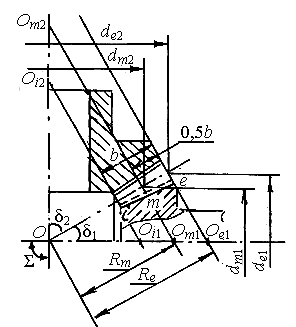
| Расстояние между внешним (параметры обозначают с индексом е) и внутренним (параметры – с индексом i) дополнительными конусами определяет ширину b венца. На длине 0,5b расположен средний дополнительный конус с вершиной Оm (параметры – с индексом m). Расстояние от вершины О по образующей делительного конуса до внешнего торца е называют внешним конусным расстоянием Re , до середины ширины венца – средним конусным расстоянием Rm (рис. 10). Пересечения делительного конуса с дополнительными конусами определяют диаметры делительных окружностей ко-нического зубчатого колеса: de – внешний, dm – средний, di – внутренний делительные диаметры.- |
Рис. 10 |
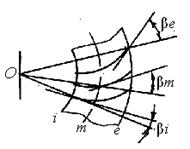
Угол наклона зубьев β определяют (рис. 11) углом между лучом, проведенным из вершины О, и касательной к линии зуба в рассматриваемой точке зуба. Для прямых зубьев β = 0. У круговых зубьев угол β переменный:
βe > βm > βi. За расчетный принимают угол βm в среднем сечении.
Рис. 11 |
Рис. 12 Лучше всего зарекомендовали себя передачи с круговыми зубьями с углом βm = 35°. |
Наличие угла наклона повышает плавность работы, контактную и изгибную прочность, уменьшает шум, но увеличивает нагрузки на опоры и валы.
Зубья конических колес в зависимости от изменения размеров их нормальных сечений по длине выполняют в виде трех осевых форм (рис. 12).
Осевая форма I - пропорционально понижающиеся зубья (рис. 12, а). Вершины конусов делительного и впадин совпадают, высота ножки зуба пропорциональна конусному расстоянию. Применяют для прямых зубьев.
Осевая форма II – нормально сужающиеся зубья (рис. 12, б). Вершина конуса впадин Оf расположена так, что ширина дна впадины колеса постоянна, а толщина зуба по делительному конусу пропорциональна конусному расстоянию. Эта форма позволяет одним инструментом обрабатывать сразу обе грани зубьев, повышая производительность. Является основной для колес с круговыми зубьями, особенно в массовом производстве.
Осевая форма III – равновысокие зубья (рис.12, в). Образующие конусов делительного, впадин и вершин параллельны. Высота зуба постоянна по всей длине. Применяют для передач с межосевым углом Σ меньше 40° и круговыми зубьями при (z12 + z22)1/2 ≥ 60.
За расчетное сечение конической передачи принято среднее сечение m.
Для удобства измерения размеры конических колес принято определять по внешнему торцу е зуба.
Различают внешний окружной модуль mtе, средний окружной модуль mtm (для прямых зубьев), средний нормальный модуль круговых зубьев mnm.
Связь между модулями:
mtе = mtm / (1 – 0,5Кbe); mtе = mnm / [(1 – 0,5Кbe)cosβm];
mnm = mtе(1 – 0,5 Кbe) cosβm,
где Кbe = b / Re – коэффициент ширины зубчатого венца по внешнему конусному расстоянию; принимают Кbe ≤ 0,3. Для большинства передач Кbe = 0,285;
βm – угол наклона зуба в среднем сечении.
Для прямых зубьев стандартным (ГОСТ 9563-60) является модуль mtе. В передачах с круговыми зубьями допускается не округлять модули по стандарту, так как одной и той же зуборезной головкой можно нарезать зубья в определенном интервале модуля за счет наладки резцов в головке. Модуль следует вычислять с точностью 0,0001 мм.
Диаметры делительных окружностей:
de = mtеz; dm = mtmz = mnmz / cosβm .
Внешнее конусное расстояние
Re = [(0,5de1)2 + (0,5de2)2]1/2 = 0,5de1(1 + u2)1/2.
Ширина зубчатого венца
b = Кbe Re = 0,285∙0,5de1(1 + u2)1/2 = 0,143de1(1 + u2)1/2.
Передаточное число
и = de2 / de1 = dm2 / dm1 = z2 / z1 = 2Resinδ2 / (2Resinδ1) = sinδ2 / sinδ1.
При δ1 + δ2 = 90О, где δ – углы делительных конусов, имеем δ1 = 90О – δ2 и тогда и = tgδ2. Так же δ2 = 90О – δ1 и и = сtgδ1.
Для передачи с круговыми зубьями профили зубьев конических колес в среднем нормальном сечении близки к профилям зубьев эквивалентных цилиндрических прямозубых колес. Приведение к последним осуществляют в два этапа:
1. К эквивалентным цилиндрическим косозубым колесам с углом наклона зубьев βm;
2. От них к эквивалентным прямозубым цилиндрическим колесам.
Из-за двойного приведения параметры называют биэквивалентными:
mv = mnm; bv = b; dvnm = dm / (cosδcos2βm); zvnm = z / (cosδcos3βm);
иv = zvnm2 / zvnm1 = z2cosδ1cos3βm / (z1cosδ2cos3βm) = (z2 / z1)tgδ2 = u2.
Для прямых зубьев в приведенных формулах следует принять βm= 0.
6.2 Силы в зацеплении
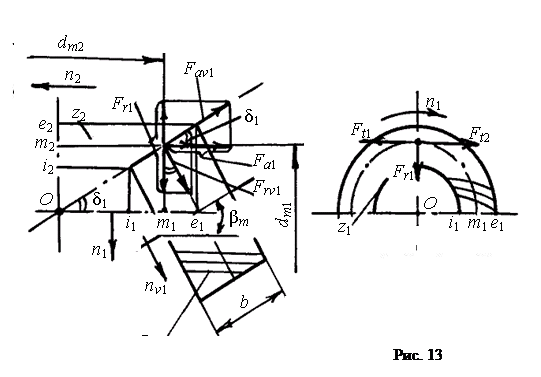 |
1. Окружная сила (рис. 13) Ft = 2000Т / dm.
2. Радиальная сила на шестерне Fr1, равная осевой силе на колесе Fа2:
Fr1 = Fа2 = Ft (tgαncosδ1 m sinβmsinδ1) / cosβm. (13)
3. Осевая сила на шестерне Fа1, равная радиальной силе на колесе Fr2:
Fа1 = Fr2 = Ft (tgαnsinδ1 ± sinβmcosδ1) / cosβm, (14)
где в формулах (13) и (14) αn – средний нормальный угол зацепления (αn ≈ 20°); βm = 35° – средний угол наклона зуба; δ1 – угол делительного конуса шестерни.
Знаки в скобках:
если смотреть с вершины делительного конуса О, то при совпадении вращения и наклона зубьев – верхние знаки, при отсутствии совпадения – нижние.
Знаки результата:
во избежание заклинивания зубьев при значительных зазорах в подшипниках необходимо обеспечить направление осевой силы Fа1 от вершины к внешнему торцу е1, т.е. сила Fа1 должна быть положительной. Это возможно при совпадении вращения и наклона зубьев.
Нормальная сила в зацеплении Fn = Ft / (cosαncosβm).
Для прямых зубьев в формулах сил следует положить βm = 0:
1) Ft1 = Ft2 = 2000Т / dm; 2) Fr1 = Fа2 = Fttgα cosδ1;
3) Fа1 = Fr2 = Fttgα sinδ1; 4) Fn = Ft / cosα.
Похожие работы
... Направление линии зуба правое. Вращение против часовой стрелки. при bm=35° при bm=35° Направление линии зуба левое. Вращение по часовой стрелке. 7. РАСЧЁТ ЧЕРВЯЧНОЙ ПЕРЕДАЧИ 7.1 Выбор материалов червяка и червячного колеса Для изготовления червяков применяют углеродистые и легированные стали (см. табл. 3.1). Выбор марки стали зависит от назначаемой термообработки ...
... …….…………………………………………………………..7 5. Последовательность проектного расчета закрытых конических прямозубых передач……………………………………………………….20 6. Последовательность проектного расчета червячных передач...……..24 Библиографический список……………………………………………….31 1. Цель и задачи курсового проектирования Курсовое проектирование является заключительным этапом в изучении общеинженерных курсов «Прикладная ...
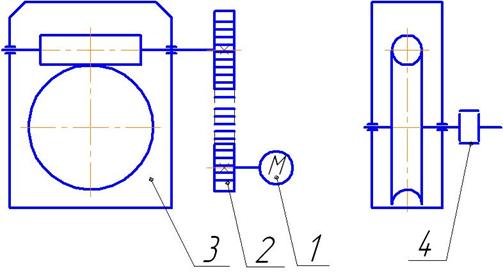
... посадок отдельных деталей. В местах посадки подшипников при вращении внутреннего кольца рекомендуют поля допусков для вала n6, m6, k6. Свободные размеры принимают по 14 квалитету. 3.2 Кинематическая схема мотор-редуктора и силы, действующие в зацеплениях зубчатых колес. Кинематическая схема трехступенчатого мотор - редуктора включает в себя червячную, коническую и цилиндрическую прямозубые ...
... валы червячного редуктора (рис.7): Рис.7 Схема усилий, действующих на валы червячного редуктора Определяем консольную нагрузку на муфте [1,табл.6.2]: ; (10.1) Н Для определения консольной нагрузки на шкиве необходимо произвести расчет зубчато-ременной передачи.[1]. Определяем минимальный диаметр ведущего шкива по диаметру ...


0 комментариев