Навигация
4.1 Примеры
Пример 4-1
Два моля гелия (идеальный газ, мольная теплоемкость
Ср = 5/2R) нагревают от 100 до 200°С при р = 1 атм. Вычислите изменение энергии Гиббса в этом процессе, если известно значение энтропии гелия,
S°373 = 131,7 Дж*К-1*моль-1. Можно ли считать этот процесс самопроизвольным?
Решение:
Изменение энергии Гиббса при нагревании от 373 до 473 К можно найти, проинтегрировав частную производную по температуре:
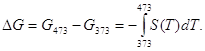
Зависимость энтропии от температуры при постоянном давлении определяется изобарной теплоемкостью:
![]()
Интегрирование этого выражения от 373 К до Т дает:

Подставляя это выражение в интеграл от энтропии, находим:
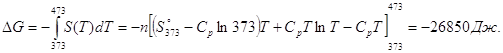
Процесс нагревания не обязан быть самопроизвольный, т.к. уменьшение энергии Гиббса служит критерием самопроизвольного протекания процесса только при Т = const и р = const.
Ответ: -26850 Дж.
Пример 4-2
Рассчитайте изменение энергии Гиббса в реакции:
СО + 1/2О2 = СО2
при температуре 500 К и парциальных давлениях 3 бар. Будет ли эта реакция самопроизвольной при данных условиях? Газы считать идеальными. Необходимые данные возьмите из справочника.
Решение:
Термодинамические данные при температуре 298 К и стандартном давлении 1 бар сведем в таблицу:
| Вещество | Энтальпия образования DfН°298 , кДж*моль-1 | Энтропия S°298 , Дж*К-1*моль-1 | Теплоемкость Ср, Дж*К-1*моль-1 |
| СО | -110,5 | 197,6 | 29,14 |
| О2 | 0 | 205,0 | 29,40 |
| СО2 | -393,5 | 213,7 | 34,57 |
| Реакция | DrН°298 , кДж/моль | DrS°298, Дж*К-1*моль-1 | DrСp, Дж*К-1*моль-1 |
| СО + ½ О2 = СО2 | -283,0 | -86,4 | -9,27 |
Примем, что DrСp= соnst. Изменения термодинамических функций в результате реакций рассчитаны как разность функций реагентов и продуктов:
Df = f(СО2) - f(СО) – 1/2 f(О2).
Стандартный тепловой эффект реакции при 500 К можно рассчитать по уравнению Кирхгофа в интегральной форме:
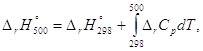
DrН°500 = -283000 + (-9,27)(500 – 298) = -284,9 кДж*моль-1
Стандартное изменение энтропии в реакции при 500 К можно рассчитать по формуле:

DrS°500=(-86,4+(-9,27)ln(500/298))Дж*К-1*моль-1=
=-91,2Дж*К-1*моль-1
Стандартное изменение энергии Гиббса при 500 К:
DrG°500 = DrН°500 - 500DrS°500,
DrG°500 = (-284900 – 500(-91,2)) кДж*моль-1=-239,3кДж*моль-1.
Рассчитаем изменение энергии Гиббса при парциальных давлениях 3 атм:
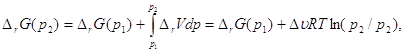
DrG(р2) = - 240200 + (-0,5)8,31*500*ln(3) = -242,5 кДж*моль-1.
Эта реакция может протекать самопроизвольно при данных условиях.
Ответ: DrG = -242,5 кДж*моль-1.
4.2 Задачи
4-1. Вычислите изменение Н, U, F, G, S при одновременном охлаждении от 2000 К до 200 К и расширении от 0,5 м3 до 1,35 м3 0,7 молей азота (СV = 5/2R). Энтропия газа в исходном состоянии равна 213,4 Дж*К-1*моль-1, газ можно считать идеальным.
(DН = -36,66 кДж, DU = -26,19 кДж, DF = 249,4 кДж,
DG = 238,9 кДж, DS = -27,72 Дж*К-1)
4-2. Рассчитайте DG° при 25°С для химической реакции: 4НСl(г) + О2(г) = 2Cl2 + 2Н2О(ж). Стандартные значения энтальпии образования и абсолютной энтропии при 25°С равны: DfН°(НСl) = -22,1 ккал*моль-1,
S°(O2) = 49,0 кал*К-1*моль-1, DfН°(Н2О(ж)) = -68,3 ккал*моль-1, S°(Сl2) = 53,3 кал*К-1*моль-1, S°(НCl) = 44,6 кал*К-1*моль-1,
S°(Н2O(ж)) = 49,0 кал*К-1*моль-1.
(DG° = -22,2 ккал*моль-1)
4-3. Вычислите изменение энергии Гиббса при сжатии
0,7*10-2 кг N2 при 300 К и давлении от 5,05*104 до 3,031*105 Па (считать азот идеальным газом).
4-4. Вычислите DG°298 для реакции
С(графит) + 2Н2(г) = СН4(г).
Определите DН°298 из следующих термохимических уравнений:
СН4(г) + 2О2(г) = СО2(г) + 2Н2О(ж) + DН°298,
СО2(г) = С(графит) + О2(г) - DН°298,
2Н2О(ж) = 2Н2(г) + О2(г) - 2DН°298.
Значение DS°298 вычислите с помощью постулата Планка.
4-5. Рассчитайте стандартные энергии Гиббса и Гельмгольца при 700°С для химической реакции:
СаСО3(тв) = СаО(тв) + СО2(г).
Теплоемкости веществ считать постоянными.
(DrG°973 = 24,4 кДж*моль-1, DrF°973 = 16,3 кДж*моль-1)
4-6. Вычислите изменение DG° для 1 моль NН3 в процессе изобарического нагревания (Р = 1,013*105 Па) от Т1 = 300 до Т2 = 400 К, если Ср = соnst. (-17,467 кДж*К-1*моль-1)
4-7. Найдите энергию Гиббса образования NН3 при температурах 298 и 400 К, если известны следующие данные: DfН°298(NН3) = -46,2 кДж*моль-1,
| Вещество | N2 | Н2 | NH3 |
| Сp,298, Дж*К-1*моль-1 | 29,1 | 28,8 | 35,7 |
| S°298 , Дж*К-1*моль-1 | 191,5 | 130,6 | 192,5 |
Считать, что теплоемкости в указанном интервале температур постоянны.
(DfG°298(NH3) = -16,7 кДж*моль-1, DrG°400(NH3) = -6,19 кДж*моль-1)
Литература
1) Г.С. Каретников, И.В. Кудряшов. Сборник примеров и задач по физической химии. - М: Высшая школа, 1991 г.
2) И.И. Климов, А.И. Филько. Сборник примеров и задач по физической и коллоидной химии. – М: Просвещение, 1975 г.
3) В.В. Еремин, С.И. Каргов, И.А. Успенская, Н.Е. Кузьменко, В.В. Лунин. Основы физической химии. Теории и задачи. – М: Экзамен, 2005.
Похожие работы
... и химическим процессам, происходящим в веществе, в различных системах. Важным достижением на пути этого процесса интеграции знаний было открытие фундаментального закона природы - закона сохранения и превращения энергии. Основатель термодинамики С. Карно в своем труде "Размышления о движущей силе огня и о машинах, способах развивать эту силу" пишет: "Тепло - это не что иное, как движущая сила, ...
... газов в результате реакции. Величина Δn может иметь положительное и отрицательное значения, в зависимости от того, увеличивается или уменьшается число молей газов во время процесса. Применение первого начала термодинамики к процессам в любых системах. Закон Гесса Примем, что единственным видом работы, которая совершается системой, является работа расширения. Подставляя уравнение (II, 5) в ...
... , или термодинамическое равновесие, при котором движение частиц хаотично. Максимальная энтропия означает полное термодинамическое равновесие, что эквивалентно хаосу. Часто второе начало термодинамики преподносится как объединенный принцип существования и возрастания энтропии. Принцип существования энтропии формулируется как математическое выражение энтропии термодинамических систем в условиях ...
... в ходе реакции мало, т.е. , тогда ; . При термомеханическом описании реакции опускают , , говорят только об изменении энтальпии : Закон Гесса: тепловой эффект химической реакции протекающий или при или при не зависит от числа промежуточных стадий, а определяется лишь конечным и начальным состоянием системы. Тепловой ...
0 комментариев