Уравнение состояния
Внутренняя энергия системы. Работа и теплота
Уравнение адиабаты идеального газа
Термохимические уравнения
Зависимость теплового эффекта химической реакции от температуры
Закон Джоуля
Уравнение Клапейрона-Клаузиуса
Определения
Условия равновесия в многокомпонентных гетерогенных системах
Навигация
Определения
Основы термодинамики
40166
знаков
3
таблицы
4
изображения
7.1. Определения.
Раствором называется гомогенная, молекулярно-дисперсная система, состав которой можно изменять непрерывно в некотором конечном или бесконечном интервале.
По агрегатному состоянию растворы разделяются на твердые, жидкие и газообразные. Если растворитель и растворенное вещество имеют разные агрегатные состояния, то растворителем рассматривают обычно то вещество, агрегатное состояние которого совпадает с агрегатным состоянием раствора. Если же компоненты раствора и раствор имеют одинаковое агрегатное состояние, то за растворитель считают то вещество, которого больше, хотя для термодинамики это безразлично.
Состав раствора измеряется его концентрацией. Существуют следующие основные определения концентрации:
мольная доля (х) – число молей вещества в 1 моле раствора;
моляльность (m) – число молей растворенного вещества в 1000 г растворителя;
молярность (с) – число молей растворенного вещества в 1 л раствора;
массовое содержание (р) – число грамм растворенного вещества в 100 г раствора.
В основном мы будем пользоваться мольной долей. Очевидно, что
, а 
.
Если М0 и М мольные массы растворителя и растворенного вещества, а d – плотность раствора, г/см3, то переход от одной концентрации к другой можно представить следующими формулами (раствор, естественно, бинарный):
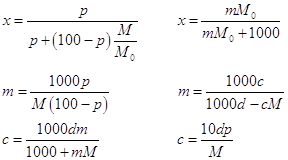
7.2. Характеристические функции многокомпонентных систем.
Первый и второй законы термодинамики, из которых следуют фундаментальные уравнения, были получены для закрытых систем, т.е. систем, процессы в которых не приводят к изменению количества компонентов. Реально же чаще встречаются системы, в которых при различных процессах изменяются количества компонентов. Это может происходить, скажем, при фазовых превращениях или вследствие протекания химической реакции. При этом может изменяться состав, как отдельных частей, так и системы в целом.
Поэтому внутренняя энергия (и другие функции состояния) открытых систем будут изменяться не только за счет сообщения системе теплоты и произведенной системой работы, но и за счет изменения состава системы. Следовательно для открытых систем характеристические функции будут функциями не только их двух естественных переменных, но и функциями числа молей всех веществ , составляющих систему:
U = U ( S, v, n1……………….nk ),
H = H ( S, p, n1 ………….. nk ),
F = F ( T, v, n1…………… nk ),
G = G ( T, p, n1……………nk ).
Полный дифференциал внутренней энергии открытой системы можем записать как: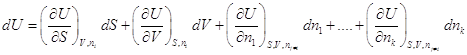
. Индекс nj≠i означает, что число молей других веществ, кроме данного, не изменяется.
Но если открытая система изменяет свое состояние при постоянном составе (все ni =const), то она ничем не отличается от закрытой системы, поэтому:
и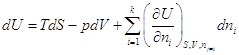 
.
Гиббс назвал частную производную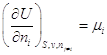 
химическим потенциалом i – компонента.
Аналогично: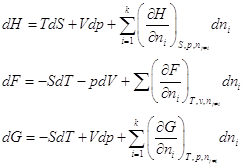 
.
Поскольку H≡ U + pV, F ≡ U – TS, G ≡ U – TS + pv, то dH = dU + pdV + Vdp, dF = dU – TdS – SdT, dG = dU – TdS – SdT + Vdp + pdV.
и подставив сюда 
получаем: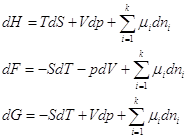 
Сравнив выражение для полных дифференциалов характеристических функций, получаем: 
,
т.е. химический потенциал компонента равен приращению характеристической функции системы при добавлении одного моля данного компонента при условии, что естественные переменные и состав системы остаются постоянными, т.е. система достаточно велика.
7.3. Однородные функции. Уравнение Гиббса-Дюгема.
Функция многих переменных, например F(x,y,z), называется однородной функцией порядка k, если она обладает следующим свойством:
F (tx, ty, tz) = tk F (x, y, z),
(например, F = x3 +x2y + y2x + z3 является однородной функцией 3-его порядка). Однородные функции обладают следующим свойством (теорема Эйлера): 
.
Доказательство теоремы Эйлера следующее:
Если f = f (x1, x2,…xn ), а каждое xi = φ(t), то 
.
Пусть F (x, y, z ) - однородная функция порядка k, положим x = tα, y=tβ, z = tγ, тогда 
.
Продифференцируем по t: 
.
Положим t = 1,тогда α = x, β = y, γ = z и 
, что и требовалось доказать.
Если температура и давление постоянны, то энергия Гиббса является функцией только числа молей компонентов: G = G (n1, n2, …nk ) и легко сообразить, что она является однородной функцией первого порядка относительно числа молей компонентов и по теореме Эйлера (k = 1):
.
После дифференцирования имеем: 
.
Но 
, а при p, T =const 
.
Следовательно, 
.
Это уравнение называется уравнением Гиббса-Дюгема и широко применяется в термодинамике растворов поскольку дает возможность рассчитать dμi i –ого компонента, если известны изменения химических потенциалов всех остальных компанентов в изобарно-изотермическом процессе. Для бинарного раствора 
.
Разделив на сумму п1 +п2, получим: 
.
Похожие работы
... тем существенным фактором, который отличает необратимые процессы в изолированных системах от аналогичных процессов в неизолированных, или открытых, системах. Второе начало термодинамики и утверждение о возрастании энтропии при любом необратимом процессе было сформулировано именно для изолированных систем. Значит, нельзя просто переносить его на неизолированные системы. Чтобы перейти к описанию ...
... и химическим процессам, происходящим в веществе, в различных системах. Важным достижением на пути этого процесса интеграции знаний было открытие фундаментального закона природы - закона сохранения и превращения энергии. Основатель термодинамики С. Карно в своем труде "Размышления о движущей силе огня и о машинах, способах развивать эту силу" пишет: "Тепло - это не что иное, как движущая сила, ...
... , или термодинамическое равновесие, при котором движение частиц хаотично. Максимальная энтропия означает полное термодинамическое равновесие, что эквивалентно хаосу. Часто второе начало термодинамики преподносится как объединенный принцип существования и возрастания энтропии. Принцип существования энтропии формулируется как математическое выражение энтропии термодинамических систем в условиях ...
... . Но публикация этого вывода была осуществлена уже после признания закона сохранения энергии, поэтому данный вывод не сыграл той роли. которую мог сыграть, будучи опубликованным ранее. Но так или иначе Карно заложил основы термодинамики как раздела физики, изучающего наиболее общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между ...
0 комментариев