Уравнение состояния
Внутренняя энергия системы. Работа и теплота
Уравнение адиабаты идеального газа
Термохимические уравнения
Зависимость теплового эффекта химической реакции от температуры
Закон Джоуля
Уравнение Клапейрона-Клаузиуса
Определения
Условия равновесия в многокомпонентных гетерогенных системах
Навигация
Условия равновесия в многокомпонентных гетерогенных системах
Основы термодинамики
40166
знаков
3
таблицы
4
изображения
7.4. Условия равновесия в многокомпонентных гетерогенных системах.
Пусть р, Т = Const, тогда 
. Если в системе имеются фазы (') и (''), то при переходе dni молей i –ого компонента из фазы (') в фазу ('') изменение энергии Гиббса системы dG будет складываться из изменении энергий Гиббса обеих фаз dG ' и dG '': 
.
Если система закрытая, то 
, а если она к тому же и равновесна, то dG = 0 и, следовательно, 
, т.е. химические потенциалы данного компонента во всех фазах системы, находящейся в равновесии, равны между собой.
Самопроизвольный неравновесный процесс может идти только в сторону уменьшения энергии Гиббса системы dG < 0 (p, T = const).
Предположим, что 
, т.е. фаза (') теряет i –ый компонент, но 
, значит 
.
Если же 
, тогда 
. Таким образом, компонент самопроизвольно переходит из фазы, в которой его химический потенциал больше, в фазу, в которой его химический потенциал меньше.
Эти условия равновесия и самопроизвольности процессов переноса вещества в многокомпонентных системах являются обобщением таковых для однокомпонентных систем (см. гл. 6). Кроме того, легко заметить, что химический потенциал чистого вещества равен его мольной энергии Гиббса.
Глава 8. Термодинамика смесей идеальных газов.
8.1. Характеристические функции идеального газа.
Для адиабатического процесса в системе (Q = 0) мы можем записать ΔU= -A.
Если идеальный газ расширяется адиабатически от объема V и температуры T до бесконечно большого объема, то он совершает работу:
,
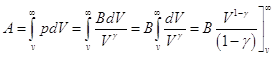а поскольку 
, то подстановка верхнего предела дает 0, подстановка нижнего приводит к 
,
.
Следовательно 
, а поскольку 
, то внутренняя энергия идеального газа, имеющего данную температуру, равна U = CVT.
Очевидно, поскольку для идеального газа dU = CV dT, то по первому закону для идеального газа: dQ = CVdT + pdV.
Разделив правую и левую часть на Т, получим 
.
Интегрирование дает 
.
Константа интегрирования S0 не зависит ни от температуры, ни от давления или объема. Как мы увидим позднее для любого вещества в состоянии идеального газа в константу S0 в качестве характеристики вещества входит только его мольная масса. Далее:
H = U + pV = U + RT = CVT +RT = CpT,
F = U – TS = CVT – TS0 - CVT ln T –RT ln V,
G = H – TS = CpT – T( S0 + R ln R ) – CpT ln T + RT ln p,
Легко видеть, что, вообще говоря,
F = F (T) – RT ln V, G = G (T ) + RT ln p,
где F (T) и G (T) - являются функциями только температуры.
8.2. Химический потенциал газа в смеси идеальных газов.
Смешение газов – самопроизвольный процесс, происходящий вследствие диффузии. Дальтон (1801) отметил, что если взятые газы имеют одинаковую температуру и давление, то в отсутствие химической реакции а) объем смеси равен сумме объемов составляющих газов в) температура остается постоянной в течение процесса. Т.е., если исходные объемы смешивающихся газов равны Vii , то общий объем смеси равен 
. Отметим, что Vii = ni Vi , где ni –число молей газа i, Vi – мольный объем его до процесса смешения. Поскольку давление р в процессе смешения не меняется, то для смеси 
, а для i – газа, занимающего объем смеси V, парциальное давление pi: piV = niRT, следовательно
. Обозначим индексом i мольные свойства i – ого газа. Тогда для смеси газов:
и, следовательно,
,
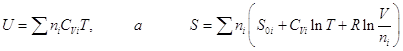и энергия Гельмгольца смеси:
.
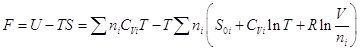Теперь становится возможным вычислить химический потенциал i – ого газа: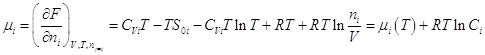 
где 
- функция только температуры, а 
- концентрация i - ого газа. Поскольку для смеси , то 
,
и химический потенциал i –ого газа можно выразить через другие величины:
.
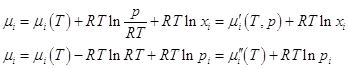Очевидно, что μi(T) – химический потенциал газа, когда Ci = 1; μ' (T,p) – химический потенциал, когда xi = 1, т.е. это мольная энергия Гиббса чистого газа i; μ''(T) – химический потенциал i - ого газа при pi = 1.
8.3. Энтропия смешения.
Энтропия смеси газов равна (см. выше):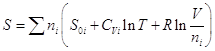 
, но 
.
Поскольку газ i имел до смешения давление p и объем Vii = nVi, имеем:
, и энтропия смеси тогда: 
.
Полином в скобках представляет собой мольную энтропию газа i до процесса смешения, поэтому сумма есть не что иное, как энтропия системы до процесса смешения, следовательно, изменение энтропии системы в результате смешения газов 
или в расчете на 1 моль смеси:
.
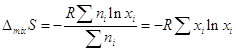Поскольку 
, то работа, которую можно получить в результате обратимого процесса смешения газов: 
.
Очевидно, что для разделения смеси газов на компоненты нужно затратить работу 
.
Однако, это только теоретическая величина, практически затрачиваемая работа будет намного больше, причем, чем меньше отличаются по свойствам компоненты, тем большая потребуется работа.
Например, разделение изотопов урана осуществляют, используя гексафторид урана. Природная смесь содержит 99,3 % U238 F6 и 0,7 % U235F6. Так вот теоретически необходимо затратить 0,023 квт·час на выделение 1 кг U235F6, практически приходится затрачивать 1,2·106 квт·час или в 50·106 раз больше.
Мы видим также, что возрастание энтропии при смешении газов зависит только от количества молей этих газов, но не зависит от их природы. В предельном случае, когда смешивается один и тот же газ, разделенный сначала перегородкой на две части, увеличения энтропии не должно быть, так как в этом случае после удаления перегородки никакого термодинамического процесса в системе не происходит. Таким образом, смешение идентичных газов нельзя рассматривать как предельный случай смешения различных газов. Легко сообразить, что если смешиваемые газы имели до смешения одинаковое давление р, то после смешения они имеют парциальные давления pi <p, а если газы идентичны, то давление не меняется. При переходе от образования смеси сколь угодно близких (разделимых) газов к смеси одинаковых газов величина ΔmixS испытывает скачок. Это утверждение получило название парадокса Гиббса.
Похожие работы
... тем существенным фактором, который отличает необратимые процессы в изолированных системах от аналогичных процессов в неизолированных, или открытых, системах. Второе начало термодинамики и утверждение о возрастании энтропии при любом необратимом процессе было сформулировано именно для изолированных систем. Значит, нельзя просто переносить его на неизолированные системы. Чтобы перейти к описанию ...
... и химическим процессам, происходящим в веществе, в различных системах. Важным достижением на пути этого процесса интеграции знаний было открытие фундаментального закона природы - закона сохранения и превращения энергии. Основатель термодинамики С. Карно в своем труде "Размышления о движущей силе огня и о машинах, способах развивать эту силу" пишет: "Тепло - это не что иное, как движущая сила, ...
... , или термодинамическое равновесие, при котором движение частиц хаотично. Максимальная энтропия означает полное термодинамическое равновесие, что эквивалентно хаосу. Часто второе начало термодинамики преподносится как объединенный принцип существования и возрастания энтропии. Принцип существования энтропии формулируется как математическое выражение энтропии термодинамических систем в условиях ...
... . Но публикация этого вывода была осуществлена уже после признания закона сохранения энергии, поэтому данный вывод не сыграл той роли. которую мог сыграть, будучи опубликованным ранее. Но так или иначе Карно заложил основы термодинамики как раздела физики, изучающего наиболее общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между ...
0 комментариев