Навигация
Метод прогонки решения разностной задачи для уравнений параболического типа
1.2 Метод прогонки решения разностной задачи для уравнений параболического типа
Рассмотрим частный случай задачи, поставленной в предыдущем разделе. В области
![]()
найти решение уравнения
![]() (1.10)
(1.10)
с граничными условиями
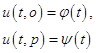 (1.11)
(1.11)
и начальным условием
![]() . (1.12)
. (1.12)
Рассмотрим устойчивую вычислительную схему, для которой величина ![]() не является ограниченной сверху, а, значит, шаг по оси
не является ограниченной сверху, а, значит, шаг по оси ![]() и
и ![]() может быть выбран достаточно крупным. Покроем область
может быть выбран достаточно крупным. Покроем область ![]() сеткой
сеткой
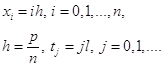
Запишем разностное уравнение, аппроксимирующее дифференциальное уравнение (1.10) во всех внутренних узлах слоя ![]() . При этом будем использовать следующие формулы:
. При этом будем использовать следующие формулы:
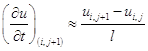 ,
,
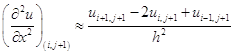 .
.
Эти формулы имеет погрешность ![]() . В результате уравнение (1.10) заменяется разностным:
. В результате уравнение (1.10) заменяется разностным:
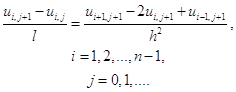 (1.13)
(1.13)
Перепишем (1.13) в виде:
![]() . (1.14)
. (1.14)
Данная вычислительная схема имеет следующую конфигурацию:
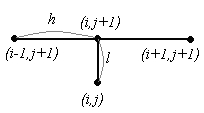
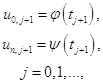 (1.15)
(1.15)
![]() (1.16)
(1.16)
Система (1.14) – (1.16) представляет собой разностную задачу, соответствующую краевой задаче (1.10) – (1.12).
За величину ![]() мы положили
мы положили ![]() .
.
(1.14) – (1.16) есть система линейных алгебраических уравнений с 3-диагональной матрицей, поэтому ее резонно решать методом прогонки, так как он в несколько раз превосходит по скорости метод Гаусса.
![]() . (1.17)
. (1.17)
Здесь ![]() ,
, ![]() – некоторые коэффициенты, подлежащие определению. Заменив в (1.17)
– некоторые коэффициенты, подлежащие определению. Заменив в (1.17) ![]() на
на ![]() будем иметь:
будем иметь:
![]() . (1.18)
. (1.18)
Подставив уравнение (1.18) в (1.14) получим:
![]() . (1.19)
. (1.19)
Сравнив (1.17) и (1.19) найдем, что:
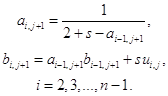 (1.20)
(1.20)
Положим в (1.14) ![]() и найдем из него
и найдем из него ![]() :
:
![]() ,
,
![]() .
.
![]() (1.21)
(1.21)
Заметим, что во второй формуле (1.21) величина ![]() подлежит замене на
подлежит замене на ![]() согласно первому условию (1.15).
согласно первому условию (1.15).
С помощью формул (1.21) и (1.20) проводим прогонку в прямом направлении. В результате находим величины
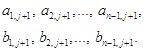
Затем осуществляем обратный ход. При этом воспользуемся второй из формул (1.15) и формулой (1.17). Получим следующую цепочку формул:
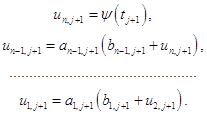 (1.22)
(1.22)
Таким образом, отправляясь от начального слоя ![]() , на котором известно решение, мы последовательно можем найти значения искомого решения во всех узлах стеки.
, на котором известно решение, мы последовательно можем найти значения искомого решения во всех узлах стеки.
Итак, мы построили неявную схему решения дифференциальных уравнений параболического типа методом сеток.
Похожие работы
... ОПИСАНИЕ ПРОГРАММЫ Поставленная задача была программно реализована на языке программирования Turbo-Pascal 7.0. В состав программы входят следующие файлы: basis.pas - PAS-файл основной части программы (решение системы уравнений методом скалярной прогонки); basis.v&v - EXE-файл основной части программы (вызывается из START.PAS); fun.bmp - BMP-фаил с изображением функций; inform.v& ...
... с единицами измерений физических величин в системе MathCAD? 11. Подробно охарактеризуйте текстовые, графические и математические блоки. Лекция №2. Задачи линейной алгебры и решение дифференциальных уравнений в среде MathCAD В задачах линейной алгебры практически всегда возникает необходимость выполнять различные операции с матрицами. Панель операторов с матрицами находится на панели Math. ...
... менять саму их постановку, вводя в нее дополнительную априорную информацию о строении решения. 2. Классификация уравнений гиперболического типа в контексте классификации уравнений математической физики Уравнения математической физики, дифференциальные уравнения с частными производными, а также некоторые родственные уравнения иных типов (интегральные, интегро-дифференциальные ...
... была построена теория вложения функциональных пространств, которые в настоящее время носят название пространств Соболева. А.Н. Тихоновым была построена теория некорректных задач. Выдающийся вклад в современную теорию дифференциальных уравнений внесли российские математики Н.Н. Боголюбов, А.Н. Колмогоров, И.Г. Петровский, Л.С. Понтрягин, С.Л. Соболев, А.Н. Тихонов и другие. Влияние на развитие ...
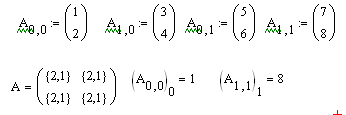

0 комментариев