Навигация
Описание логики программного модуля
2.2 Описание логики программного модуля
Листинг программы приведен в приложении 1. Ниже будут описаны функции программного модуля и их назначение.
Функция main() является базовой. Она реализует алгоритм метода сеток, описанного в предыдущих разделах работы.
Функция f (x, y) представляет собой свободную функцию двух переменных дифференциального уравнения (1.29). В качестве аргумента в нее передаются два вещественных числа с плавающей точкой типа float. На выходе функция возвращает значение функции ![]() , вычисленное в точке
, вычисленное в точке ![]() .
.
Функции mu_1 (t) и mu_2 (t) представляют собой краевые условия. В них передается по одному аргументу (t) вещественного типа (float).
Функция phi() является ответственной за начальный условия.
В функции main() определены следующие константы:
![]() – правая граница по
– правая граница по ![]() для области
для области ![]() ;
;
![]() – правая граница по
– правая граница по ![]() для области
для области ![]() ;
;
![]() – шаг сетки по оси
– шаг сетки по оси ![]() ;
;
![]() – шаг сетки по оси
– шаг сетки по оси ![]() ;
;
Варьируя ![]() и
и ![]() можно изменять точность полученного решения
можно изменять точность полученного решения ![]() от менее точного к более точному. Выше было доказано, что используемая вычислительная схема устойчива для любых комбинаций параметров
от менее точного к более точному. Выше было доказано, что используемая вычислительная схема устойчива для любых комбинаций параметров ![]() и
и ![]() , поэтому при устремлении их к нуля можем получить сколь угодно близкое к точному решение.
, поэтому при устремлении их к нуля можем получить сколь угодно близкое к точному решение.
Программа снабжена тремя механизмами вывода результатов работы: на экран в виде таблицы, в текстовый файл, а также в файл списка математического пакета Waterloo Maple. Это позволяет наглядно представить полученное решение.
Программа написана на языке программирования высокого уровня Borland C++ 3.1 в виде приложения MS-DOS. Обеспечивается полная совместимость программы со всеми широко известными операционными системами корпорации Майкрософт: MS-DOS 5.x, 6.xx, 7.xx, 8.xx, Windows 9x/Me/2000/NT/XP.
2.3 Пример работы программы
В качестве примера рассмотрим численное решение следующего дифференциального уравнения параболического типа:
![]()
в области
![]() ,
,
удовлетворяющее условиям
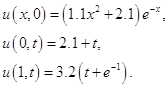
Задав прямоугольную сетку с шагом оси ![]() 0.1 и по оси
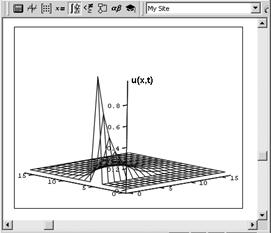
0.1 и по оси ![]() 0.01, получим следующее решение:
0.01, получим следующее решение:
2.10 1.91 1.76 1.63 1.53 1.44 1.37 1.31 1.26 1.22 1.18
2.11 1.75 1.23 1.20 1.15 1.10 1.07 1.04 1.04 1.07 1.21
2.12 1.61 0.95 0.96 0.93 0.91 0.90 0.90 0.94 1.03 1.24
2.13 1.51 0.79 0.81 0.81 0.80 0.81 0.83 0.89 1.03 1.27
2.14 1.45 0.69 0.73 0.74 0.74 0.76 0.80 0.88 1.04 1.31
2.15 1.41 0.64 0.69 0.70 0.71 0.74 0.79 0.89 1.05 1.34
В таблице ось x расположена горизонтально, а ось t расположена вертикально и направлена вниз.
На выполнение программы на среднестатистическом персональном компьютере тратится время, равное нескольким миллисекундам, что говорит о высокой скорости алгоритма.
Подробно выходной файл output.txt, содержащий таблицу значений функции ![]() представлен в приложении 3.
представлен в приложении 3.
Заключение
В работе был рассмотрен метод сеток решения параболических уравнений в частных производных. Раскрыты основные понятия метода, аппроксимация уравнения и граничных условий, исследована разрешимость и сходимость получаемой системы разностных уравнений.
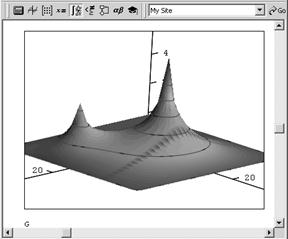
На основании изученного теоретического материала была разработана программная реализация метода сеток, проанализирована ее сходимость и быстродействие, проведен тестовый расчет, построен графики полученного численного решения.
Список источников
1. Березин И.С., Жидков Н.П. Методы вычислений. Т.2. – М.: Физматгиз, 1962.
2. Тихонов А.Н., Самарский А.А. Уравнения математической физики. – М.: Наука, 1972.
3. Пирумов У.Г. Численные методы. – М.: Издательство МАИ, 1998.
4. Калиткин Н.Н. Численные методы. – М.: Наука, 1976.
Приложение
Текст программы
// – //
#include <stdio.h>
#include <conio.h>
#include <math.h>
void main(void);
float f (float x, float t);
float mu_1 (float t);
float mu_2 (float t);
float phi (float x);
// – //
void main(void)
{
clrscr();
FILE *myfile;
FILE *plotter;
float a[120] [120];
float b[120] [120];
float u[120] [120];
float T = 0.05;
float l = 1;
float h = 0.1;
float tau = 0.01;
int n, i, j, k;
float s = pow (h, 2) / tau;
n = ceil (l / h);
for (i = 0; i <= 119; i++)
{
for (j = 1; j <= 119; j++)
{
u[i] [j] = 0;
a[i] [j] = 0;
b[i] [j] = 0;
}
}
for (i = 0; i <= n; i++)
{
u[i] [0] = phi (i * h);
}
for (j = 0; j <= floor (T /tau); j++)
{
u[0] [j] = mu_1 (tau * j);
u[n] [j] = mu_2 (tau * j);
}
for (j = 0; j <= floor (T / tau); j++)
{
a[1] [j + 1] = 1 / (2 + s);
for (i = 2; i <= n – 1; i++)
{
a[i] [j + 1] = 1 / (2 + s – a [i – 1] [j + 1]);
}
b[1] [j + 1] = mu_1 ((j + 1) * tau) + s * u[1] [j] + pow (h, 2) * f (h, (j + 1) * tau);
for (i = 2; i <= n – 1; i++)
{
b[i] [j + 1] = a [i – 1] [j + 1] + s * u[i] [j] + pow (h, 2) * f (i * h, (j + 1) * tau);
}
u[n] [j + 1] = mu_2 ((j + 1) * tau);
for (k = 1; k <= n – 1; k++)
{
u [n – k] [j + 1] = a [n – k] [j + 1] * (b [n – k] [j + 1] + u [n – k + 1] [j + 1]);
}
}
myfile = fopen («output.txt», «w+»);
plotter = fopen («3dplot.txt», «w+»);
fprintf (myfile, «Таблица значений функции u=u (x, t) в области D={0<=X<=%g, 0<=T<=%g}:\n», l, T);
printf («Значения функции u (x, t) в области D={0<=X<=%g, 0<=T<=%g}:\n\n», l, T);
for (j = 0; j <= floor (T / tau); j++)
{
for (i = 0; i <= n; i++)
{
printf («%.2f», u[i] [j]);
fprintf (myfile, «u(%g) (%g)=%g;\n», i * h, j * tau, u[i] [j]);
if (i < n && j < floor (T / tau))
{
fprintf (plotter, «[[%g, %g, %g], [%g, %g, %g], [%g, %g, %g], [%g, %g, %g]]», i * h, j * tau, u[i] [j], (i + 1) * h, j * tau, u [i + 1] [j], i * h, (j + 1) * tau, u[i] [j + 1], (i + 1) * h, (j + 1) * tau, u [i + 1] [j + 1]);
if (i >= n – 1 && j >= floor (T / tau) – 1)
{
}
else
{
fprintf (plotter,»,»);
}
}
}
printf («\n»);
}
fclose(myfile);
fclose(plotter);
printf («\nОсь x расположена горизонтально; ось t расположена вертикально и направлена вниз»);
printf («Шаг по оси x равен % g; шаг по оси t равен % g.\n», h, tau);
printf («\nДля выхода нажмите ENTER…»);
while (getch()!= 13);
}
// – //
float f (float x, float t)
{
return x * t;
}
// – //
float mu_1 (float t)
{
return 2.1 + t;
}
// – //
float mu_2 (float t)
{
return 3.2 * (t + 1 / 2.71828);
}
// – //
float phi (float x)
{
return (1.1 * pow (x, 2) + 2.1) * exp(-x);
}
Похожие работы
... ОПИСАНИЕ ПРОГРАММЫ Поставленная задача была программно реализована на языке программирования Turbo-Pascal 7.0. В состав программы входят следующие файлы: basis.pas - PAS-файл основной части программы (решение системы уравнений методом скалярной прогонки); basis.v&v - EXE-файл основной части программы (вызывается из START.PAS); fun.bmp - BMP-фаил с изображением функций; inform.v& ...
... с единицами измерений физических величин в системе MathCAD? 11. Подробно охарактеризуйте текстовые, графические и математические блоки. Лекция №2. Задачи линейной алгебры и решение дифференциальных уравнений в среде MathCAD В задачах линейной алгебры практически всегда возникает необходимость выполнять различные операции с матрицами. Панель операторов с матрицами находится на панели Math. ...
... менять саму их постановку, вводя в нее дополнительную априорную информацию о строении решения. 2. Классификация уравнений гиперболического типа в контексте классификации уравнений математической физики Уравнения математической физики, дифференциальные уравнения с частными производными, а также некоторые родственные уравнения иных типов (интегральные, интегро-дифференциальные ...
... была построена теория вложения функциональных пространств, которые в настоящее время носят название пространств Соболева. А.Н. Тихоновым была построена теория некорректных задач. Выдающийся вклад в современную теорию дифференциальных уравнений внесли российские математики Н.Н. Боголюбов, А.Н. Колмогоров, И.Г. Петровский, Л.С. Понтрягин, С.Л. Соболев, А.Н. Тихонов и другие. Влияние на развитие ...

0 комментариев