Навигация
2. Реализация метода
2.1 Разработка программного модуля
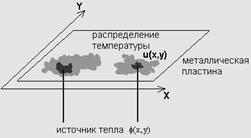
Поставлена цель: разработать программный продукт для нахождения приближенного решения параболического уравнения:
(1.29)
в области
,
удовлетворяющее условиям
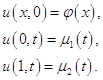(1.30)
Разобьем область 
прямыми
где
– шаг по оси 
,
– шаг по оси 
.
Заменив в каждом узле производные конечно-разностными отношениями по неявной схеме, получим систему вида:
. (1.31)
Преобразовав ее, получим:
, (1.32)
где
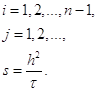
В граничных узлах
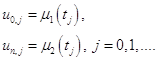(1.33)
В начальный момент
. (1.34)
Эта разностная схема устойчива при любом 
. Будем решать систему уравнений (1.32), (1.33) и (1.34) методом прогонки. Для этого ищем значения функции в узле 
в виде
, (1.35)
где 
– пока неизвестные коэффициенты.
Аналогично
. (1.36)
Подставив значение (1.35) в (1.32) получим:
.
Откуда
. (1.37)
Из сравнения (1.35) и (1.37) видно, что
. (1.38)
. (1.39)
Для 
из (1.32) имеем:
.
Откуда
или
.
Откуда, используя (1.35), получим:
, (1.40)
. (1.41)
Используя данный метод, мы все вычисления проведем в следующем порядке для всех 
.
1) Зная значения функции 
на границе (1.33), найдем значения коэффициентов 
по (1.40) и 
по (1.38) для всех 
.
2) Найдем 
по (1.41), используя для 
начальное условие (1.34).
3) Найдем по формулам (1.39) для .
4) Найдем значения искомой функции на 
слое, начиная с 
:
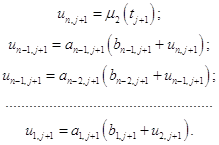
Похожие работы
... ОПИСАНИЕ ПРОГРАММЫ Поставленная задача была программно реализована на языке программирования Turbo-Pascal 7.0. В состав программы входят следующие файлы: basis.pas - PAS-файл основной части программы (решение системы уравнений методом скалярной прогонки); basis.v&v - EXE-файл основной части программы (вызывается из START.PAS); fun.bmp - BMP-фаил с изображением функций; inform.v& ...
... с единицами измерений физических величин в системе MathCAD? 11. Подробно охарактеризуйте текстовые, графические и математические блоки. Лекция №2. Задачи линейной алгебры и решение дифференциальных уравнений в среде MathCAD В задачах линейной алгебры практически всегда возникает необходимость выполнять различные операции с матрицами. Панель операторов с матрицами находится на панели Math. ...
... менять саму их постановку, вводя в нее дополнительную априорную информацию о строении решения. 2. Классификация уравнений гиперболического типа в контексте классификации уравнений математической физики Уравнения математической физики, дифференциальные уравнения с частными производными, а также некоторые родственные уравнения иных типов (интегральные, интегро-дифференциальные ...
... была построена теория вложения функциональных пространств, которые в настоящее время носят название пространств Соболева. А.Н. Тихоновым была построена теория некорректных задач. Выдающийся вклад в современную теорию дифференциальных уравнений внесли российские математики Н.Н. Боголюбов, А.Н. Колмогоров, И.Г. Петровский, Л.С. Понтрягин, С.Л. Соболев, А.Н. Тихонов и другие. Влияние на развитие ...
0 комментариев