Навигация
Семейства решений с постоянной четной частью
Министерство образования Республики Беларусь
Учреждение образования Гомельский государственный университет имени Франциска Скорины
Курсовая работа
"Семейства решений с постоянной четной частью"
Гомель, 2005
Реферат
В данной курсовой работе 17 листов. Работа состоит из пяти разделов. Ключевые слова: ДУ, решение, система, общее решение, четность, функция.
В работе содержится исследование семейства решений линейной системы. Выясняется связь семейства решений этой системы с её отражающей функцией и её свойствами. Устанавливаются условия, при которых линейная система имеет общее решение, четная часть которого не зависит от времени.
Библиография – 5 названий.
Содержание
Введение
1. Определение и свойства отражающей функции
2. Простейшая система
3. Система чет-нечет
4. Примеры систем, семейства решений которых имеют постоянную четную часть
5. Семейства решений с постоянной четной частью
Заключение
Литература
Введение
Основным инструментом нашего исследования является понятие «отражающей функции».
При изучении вопросов существования периодических решений дифференциальных систем и уравнений используются свойства симметричности (четность, нечетность и т.п.) как функций, задающих изучаемую систему, так и самих решений.
В данной работе мы будем изучать семейства решений с постоянной четной частью, когда четная часть будет представлена в виде константы.
Исследования с помощью отражающей функции позволяет получить новые результаты даже для уже хорошо изученных линейных систем.
1. Определение и свойства отражающей функции
Рассмотрим систему
![]()
![]() , (1.1)
, (1.1)
считая, что её правая часть непрерывна и имеет непрерывные частные производные по ![]() . Общее решение этой системы в форме Коши обозначим через
. Общее решение этой системы в форме Коши обозначим через ![]() . Через
. Через ![]() обозначим интервал существования решения
обозначим интервал существования решения ![]()
Пусть
![]() .
.
Определение: Отражающей функцией системы (1.1) назовем дифференцируемую функцию ![]() , определяемую формулой
, определяемую формулой ![]() (*) или формулами
(*) или формулами ![]() .
.
Для отражающей функции справедливы свойства:
1). Для любого решения ![]() , системы
, системы ![]() верно тождество
верно тождество
![]() ; (1.2)
; (1.2)
2). Для отображающей функции ![]() любой системы выполнены тождества:
любой системы выполнены тождества:
![]() ; (1.3)
; (1.3)
3). Дифференцируемая функция ![]() будет отражающей функцией системы (1.1) тогда и только тогда, когда она удовлетворяет уравнениям в частных производных
будет отражающей функцией системы (1.1) тогда и только тогда, когда она удовлетворяет уравнениям в частных производных
![]() (1.4)
(1.4)
и начальному условию
![]() . (1.5)
. (1.5)
Уравнение (1.4) будем называть основным уравнением (основным соотношением) для отражающей функции.
► Свойство 1) следует непосредственно из определения (*). Для доказательства свойства 2) заметим, что согласно свойству 1) для любого решения ![]() системы (1) верны тождества
системы (1) верны тождества ![]() . Из этих тождеств в силу того, что через каждую точку
. Из этих тождеств в силу того, что через каждую точку ![]() проходит некоторое решение
проходит некоторое решение ![]() системы (1.1), и следуют тождества (1.3).
системы (1.1), и следуют тождества (1.3).
Приступим к доказательству свойства 3). Пусть ![]() – отражающая функция системы (1.1). Тогда для неё верно тождество (1.2). Продифференцируем это тождество по
– отражающая функция системы (1.1). Тогда для неё верно тождество (1.2). Продифференцируем это тождество по ![]() и воспользуемся тем, что
и воспользуемся тем, что ![]() – решение системы (1.1), и самим тождеством (1.2). Получим тождество
– решение системы (1.1), и самим тождеством (1.2). Получим тождество
![]()
из которого в силу произвольности решения ![]() следует, что
следует, что ![]() – решение системы (1.4). Начальное условие согласно свойству 2) так же выполняется.
– решение системы (1.4). Начальное условие согласно свойству 2) так же выполняется.
Пусть некоторая функция ![]() удовлетворяет системе (1.4) и условию (1.5). Так как этой системе и этому условию удовлетворяет так же и отражающая функция, то из единственности решения задачи (1.4) – (1.5) функция
удовлетворяет системе (1.4) и условию (1.5). Так как этой системе и этому условию удовлетворяет так же и отражающая функция, то из единственности решения задачи (1.4) – (1.5) функция ![]() должна совпадать с отражающей функцией. Свойство 3) доказано.
должна совпадать с отражающей функцией. Свойство 3) доказано.
Основная лемма. Пусть правая часть системы (1.1) ![]() – периодична по
– периодична по ![]() , непрерывна и имеет непрерывные частные производные по переменным
, непрерывна и имеет непрерывные частные производные по переменным ![]() . Тогда отображение за период для системы (1.1) можно найти по формуле
. Тогда отображение за период для системы (1.1) можно найти по формуле
![]() ,
,
и поэтому решение ![]() системы (1.1) будет
системы (1.1) будет ![]() – периодическим тогда и только тогда, когда
– периодическим тогда и только тогда, когда ![]() есть решение недифференциальной системы
есть решение недифференциальной системы
![]() (1.6)
(1.6)
В качестве следствия этой леммы докажем следующее предположение. Пусть непрерывно дифференцируемая функция ![]()
![]() – периодична и нечетна по
– периодична и нечетна по ![]() , т. е.
, т. е. ![]() и
и ![]() . Тогда всякое продолжение на отрезок
. Тогда всякое продолжение на отрезок ![]() решение системы (1.1) будет
решение системы (1.1) будет ![]() – периодическим и четным по
– периодическим и четным по ![]() .
.
Для доказательства достаточно заметить, что функция ![]() удовлетворяет уравнению (1.4) и условию (1.5). Поэтому она согласно свойству 3) является отражающей функцией рассматриваемой системы. Уравнение (1.6) в нашем случае вырождается в тождество, и ему удовлетворяет любое
удовлетворяет уравнению (1.4) и условию (1.5). Поэтому она согласно свойству 3) является отражающей функцией рассматриваемой системы. Уравнение (1.6) в нашем случае вырождается в тождество, и ему удовлетворяет любое ![]() , для которого определено значение
, для которого определено значение ![]() . Согласно основной лемме любое продолжимое на
. Согласно основной лемме любое продолжимое на ![]() решение системы (1.1) будет
решение системы (1.1) будет ![]() – периодическим. Четность произвольного решения
– периодическим. Четность произвольного решения ![]() системы (1.1) следует из тождеств
системы (1.1) следует из тождеств ![]() , справедливых в силу свойства 1) отражающей функции.
, справедливых в силу свойства 1) отражающей функции.
Похожие работы
... , имеющие постоянную четную часть Пусть нам дана система (14) Перед нами стоит следующий вопрос о том, когда семейство решений этой системы будут иметь постоянную четную часть. (15) То есть, когда не будет зависеть от времени . Возьмем отражающую функцию системы (14) и используя получим четную часть следующим образом: ...
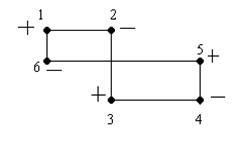
... . Система векторов условий транспортной задачи линейно независима тогда и только тогда, когда из соответствующих им клеток таблицы нельзя образовать ни одного цикла. Следовательно, допустимое решение транспортной задачи , i=1,2,…,m; j=1,2,…,n является опорным только в том случае, когда из занятых им клеток таблицы нельзя образовать ни одного цикла. Метод вычеркивания. Для проверки возможности ...
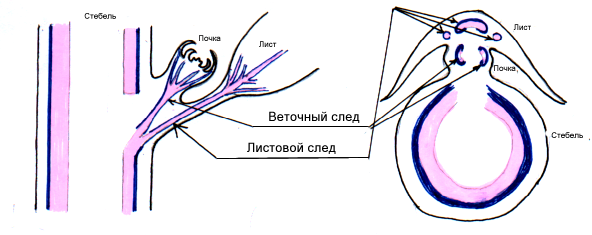
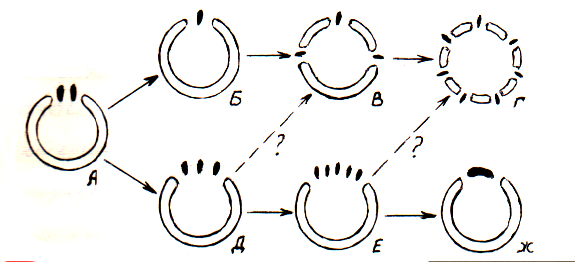
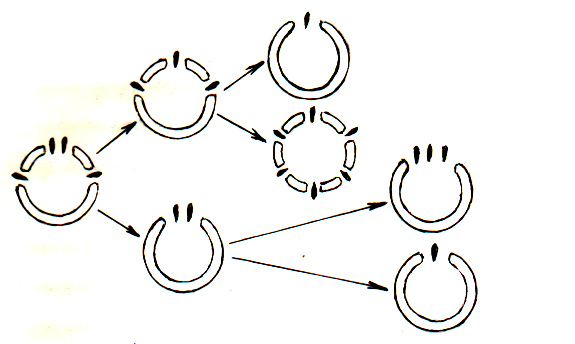
... , когда в три пучка листового следа объединяются при внедрении в лакуну центрального цилиндра. Полученные данные еще раз подтверждают ошибочность утверждения Шулькиной (1980) о том, что все представители семейства Campanulaceae обладают однолакунными однопучковыми узлами. Дальнейшие выводы можно стоить только определив строение узла у предков Campanulaceae. Если принять утверждение, что предок ...
... пользоваться и которая не подведет; - операционная система Windows XP Home Edition более удобная и более быстрая. 2. Разработка компьютерной сети на предприятии по разработке программного обеспечения 2.1 Постановка задачи Необходимо разработать локальную сеть из 70 компьютеров. Выбор технологии подключения к Интернет произволен. Удаленный участок сети необходимо разместить в диаметре 1 ...

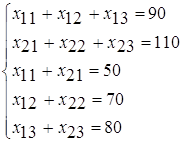
0 комментариев