Навигация
Примеры систем, семейства решений которых имеют постоянную четную часть
4. Примеры систем, семейства решений которых имеют постоянную четную часть
1![]() .
. 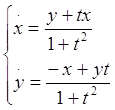
Найдем решение:
![]() ;
;
![]() ;
;
![]()
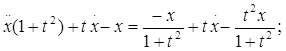
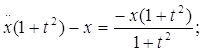
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Таким образом: 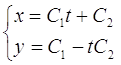
Сделаем проверку: 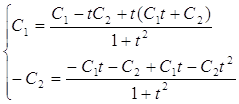
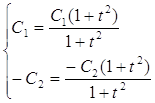 ;
; 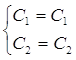
Четная часть общего решения: ![]()
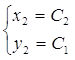
2![]() .
.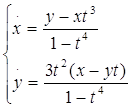
Найдем решение:
![]()
![]()
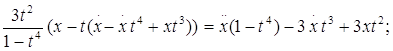
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Таким образом: 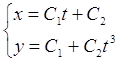
Сделаем проверку: 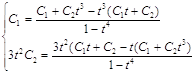 ;
;
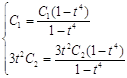 ;
;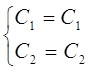 , четная часть общего решения
, четная часть общего решения 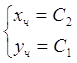
3![]() .
. 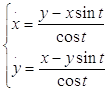
Найдем решение:
![]()
![]()
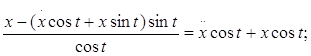
![]()
![]()
![]()
![]()
![]()
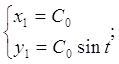
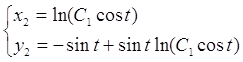 .
.
Сделаем проверку:
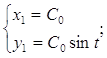
![]()
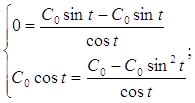
![]()
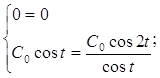
![]()
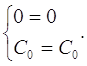
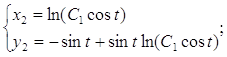
![]()
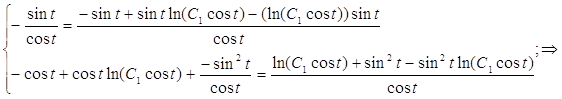
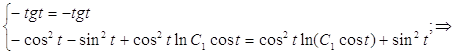
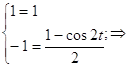
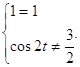 Таким образом:
Таким образом: 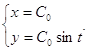 Четная часть общего решения
Четная часть общего решения
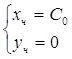
Из данных примеров можем заметить, что решения систем записывается в виде:
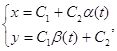
где ![]() и
и ![]() – нечетные функции, а четная часть представлена константой.
– нечетные функции, а четная часть представлена константой.
![]()
![]()
![]()
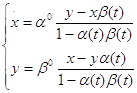 (4.1)
(4.1)
Системы вида (4.1) будут иметь семейства решений с постоянной четной частью.
5. Семейства решений с постоянной четной частью
Рассмотрим систему
![]() (5.1)
(5.1)
Надо выяснить, когда и при каких условиях семейства решений этой системы будут иметь постоянную четную часть ![]() . Иначе говоря, когда
. Иначе говоря, когда ![]() не будет зависеть от
не будет зависеть от ![]() .
.
Рассмотрим уравнение ![]() . Его решение
. Его решение
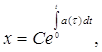
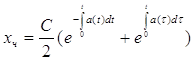 .
.
Возьмем отражающую функцию ![]() системы (5.1), тогда, используя (1.2) можем записать четную часть следующим образом:
системы (5.1), тогда, используя (1.2) можем записать четную часть следующим образом:
![]() (5.2)
(5.2)
Если четная часть будет представлена константой, то
![]() . (5.3)
. (5.3)
Продифференцируем (5.2) и прировняем к (5.3). Получаем: ![]() . Учитывая (5.1), имеем:
. Учитывая (5.1), имеем:
![]() .
.
Воспользуемся соотношением (1.4)
![]()
![]()
![]() (5.4)
(5.4)
Таким образом, приходим к теореме:
Теорема: Если система вида ![]() (5.1) имеет семейства решений с постоянной четной частью, то выполнено тождество
(5.1) имеет семейства решений с постоянной четной частью, то выполнено тождество
![]() (5.4)
(5.4)
Заключение
Мы исследовали понятие «отражающей функции».
Для периодических решений дифференциальных систем и уравнений были использованы свойства симметричности (четность, нечетность и т.д.) как функций, задающих изучаемую систему, так и самих решений.
Были изучены семейства решений с постоянной четной частью.
На примерах мы убедились, что для различных систем, семейства решений которых имеет постоянную четную часть, была получена одинаковая четная часть общего решения.
Таким образом, в работе мы исследовали семейства решений линейной системы. Выяснили связь семейства решений этой системы с её отражающей функцией и её свойствами. Установили условия, при которых линейная система имеет общее решение, четная часть которого не зависит от времени.
Литература
1. Арнольд В.И. «Обыкновенные дифференциальные уравнения», М.: Наука, 1971–240 с.
2. Бибиков Ю.Н. «Общий курс дифференциальных уравнений», изд. Ленинградского университета, 1981–232 с.
3. Еругин Н.П. «Книга для чтения по общему курсу дифференциальных уравнений. 3-е издание», М. изд. Наука и Техника, 1979–744 с.
4. Мироненко В.И. «Отражающая функция и периодические решения дифференциальных уравнений», г. Минск: изд. «Университетское», 1986–76 с.
5. Понтрягин Л.С. «Обыкновенные дифференциальные уравнения», М.: Наука, 1970–331 с.
Похожие работы
... , имеющие постоянную четную часть Пусть нам дана система (14) Перед нами стоит следующий вопрос о том, когда семейство решений этой системы будут иметь постоянную четную часть. (15) То есть, когда не будет зависеть от времени . Возьмем отражающую функцию системы (14) и используя получим четную часть следующим образом: ...
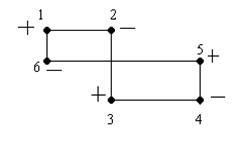
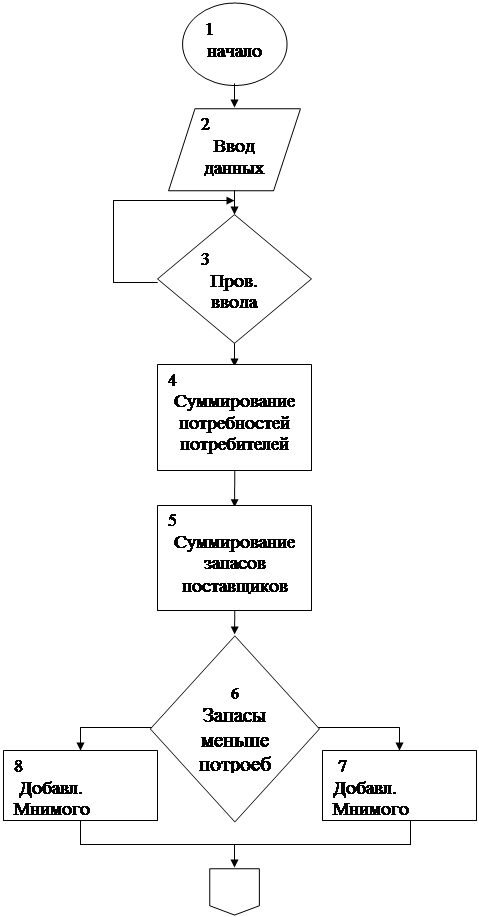
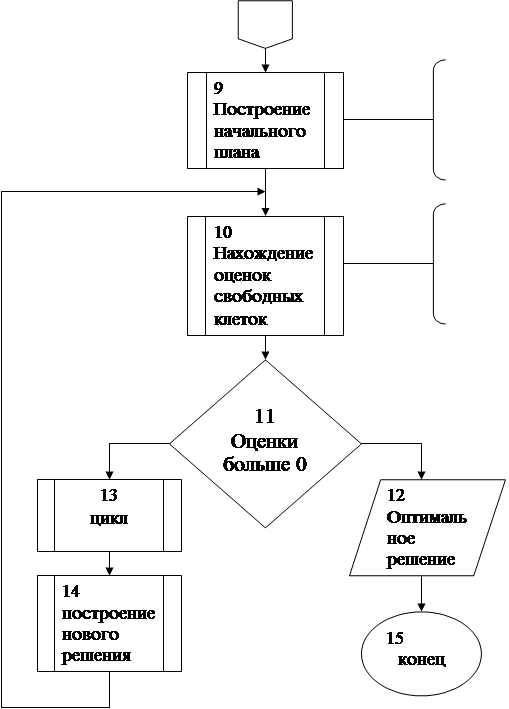
... . Система векторов условий транспортной задачи линейно независима тогда и только тогда, когда из соответствующих им клеток таблицы нельзя образовать ни одного цикла. Следовательно, допустимое решение транспортной задачи , i=1,2,…,m; j=1,2,…,n является опорным только в том случае, когда из занятых им клеток таблицы нельзя образовать ни одного цикла. Метод вычеркивания. Для проверки возможности ...
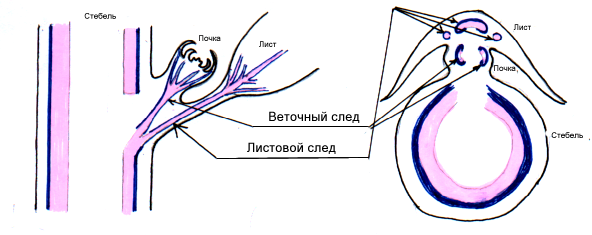
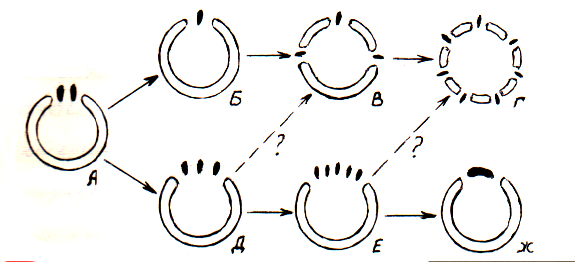
... , когда в три пучка листового следа объединяются при внедрении в лакуну центрального цилиндра. Полученные данные еще раз подтверждают ошибочность утверждения Шулькиной (1980) о том, что все представители семейства Campanulaceae обладают однолакунными однопучковыми узлами. Дальнейшие выводы можно стоить только определив строение узла у предков Campanulaceae. Если принять утверждение, что предок ...
... пользоваться и которая не подведет; - операционная система Windows XP Home Edition более удобная и более быстрая. 2. Разработка компьютерной сети на предприятии по разработке программного обеспечения 2.1 Постановка задачи Необходимо разработать локальную сеть из 70 компьютеров. Выбор технологии подключения к Интернет произволен. Удаленный участок сети необходимо разместить в диаметре 1 ...
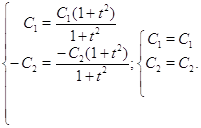
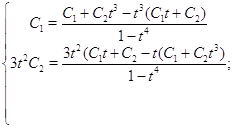

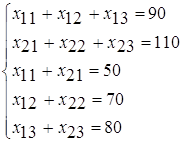
0 комментариев