Навигация
2. Простейшая система
Простейшей называют систему вида
![]() (2.1),
(2.1),
где ![]() – отражающая функция этой системы.
– отражающая функция этой системы.
Теорема: Пусть ![]() (2.2) простейшая система, тогда
(2.2) простейшая система, тогда ![]() , где
, где ![]() - отражающая функция системы (2.2).
- отражающая функция системы (2.2).
Если система простейшая,
![]() ;
;
![]() .
.
Замечание. Доказанная теорема позволяет нам определять, является данная нам система (2.2.) простейшей или нет. Для этого следует по системе (2.2.) записать соотношение (2.3.), из него определить функцию ![]() , обладающую свойством
, обладающую свойством ![]() и для неё проверить все соотношения. Если соотношения выполнены, то система простейшая.
и для неё проверить все соотношения. Если соотношения выполнены, то система простейшая.
3. Система чет-нечет
Рассмотрим систему
![]() (3.1)
(3.1)
Будем считать, что всюду в дальнейшем эта система удовлетворяет условиям:
а.) Функция ![]() непрерывно дифференцируема, и поэтому, задача Коши для системы (3.1) имеет единственное решение;
непрерывно дифференцируема, и поэтому, задача Коши для системы (3.1) имеет единственное решение;
б.) Правая часть системы (3.1) ![]() – периодична по
– периодична по ![]() .
.
Лемма. Пусть система (3.1) удовлетворяет условиям а). и б). Тогда продолжимое на отрезок ![]() решение
решение ![]() этой системы будет
этой системы будет ![]() – периодическим тогда и только тогда, когда
– периодическим тогда и только тогда, когда
![]() ,
,
где ![]() – есть нечетная часть решения
– есть нечетная часть решения ![]() .
.
Пусть ![]() –
– ![]() – периодическое решение системы (3.1). Тогда
– периодическое решение системы (3.1). Тогда ![]() . Необходимость доказана.
. Необходимость доказана.
Пусть ![]() – решение системы (3.1), для которого
– решение системы (3.1), для которого ![]() . Тогда
. Тогда ![]() , и поэтому
, и поэтому ![]() . Таким образом, точка
. Таким образом, точка ![]() есть неподвижная точка отображения за период, а решение
есть неподвижная точка отображения за период, а решение ![]() –
– ![]() – периодическое.
– периодическое.
Доказанная лемма вопрос о периодичности решения ![]() , сводит к вычислению одного из значений нечетной части
, сводит к вычислению одного из значений нечетной части![]() . Иногда относительно
. Иногда относительно ![]() можно сказать больше, чем о самом решении
можно сказать больше, чем о самом решении ![]() . Это позволяет в таких случаях делать различные заключения относительно существования периодических решений у систем вида (3.1). Дифференцируемые функции
. Это позволяет в таких случаях делать различные заключения относительно существования периодических решений у систем вида (3.1). Дифференцируемые функции ![]() ;
; ![]() , удовлетворяют некоторой системе дифференциальных уравнений. Прежде, чем выписать эту систему, заметим:
, удовлетворяют некоторой системе дифференциальных уравнений. Прежде, чем выписать эту систему, заметим:
![]() (3.2)
(3.2)
Так как ![]() решение системы (3.1). Заменяя в тождестве (3.2)
решение системы (3.1). Заменяя в тождестве (3.2) ![]() на
на ![]() и учитывая, что производная четной функции – функция нечетная, а производная нечетной функции – функция четная, получаем тождество
и учитывая, что производная четной функции – функция нечетная, а производная нечетной функции – функция четная, получаем тождество
![]() (3.3)
(3.3)
Из тождеств (3.2) и (3.3) найдем производные:
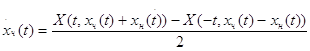 ;
;
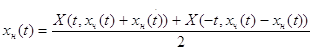 .
.
Таким образом, вектор-функция
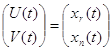 (3.4)
(3.4)
Удовлетворяет следующей системе дифференциальных уравнений порядка
![]() :
: ![]() ;
;
![]()
При этом ![]() . Систему (3.5) будем называть системой чет-нечет, соответствующей системе (3.1) решение системы чет-нечет, как следует из условия а), однозначно определяется своими начальными условиями.
. Систему (3.5) будем называть системой чет-нечет, соответствующей системе (3.1) решение системы чет-нечет, как следует из условия а), однозначно определяется своими начальными условиями.
Похожие работы
... , имеющие постоянную четную часть Пусть нам дана система (14) Перед нами стоит следующий вопрос о том, когда семейство решений этой системы будут иметь постоянную четную часть. (15) То есть, когда не будет зависеть от времени . Возьмем отражающую функцию системы (14) и используя получим четную часть следующим образом: ...
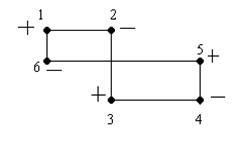
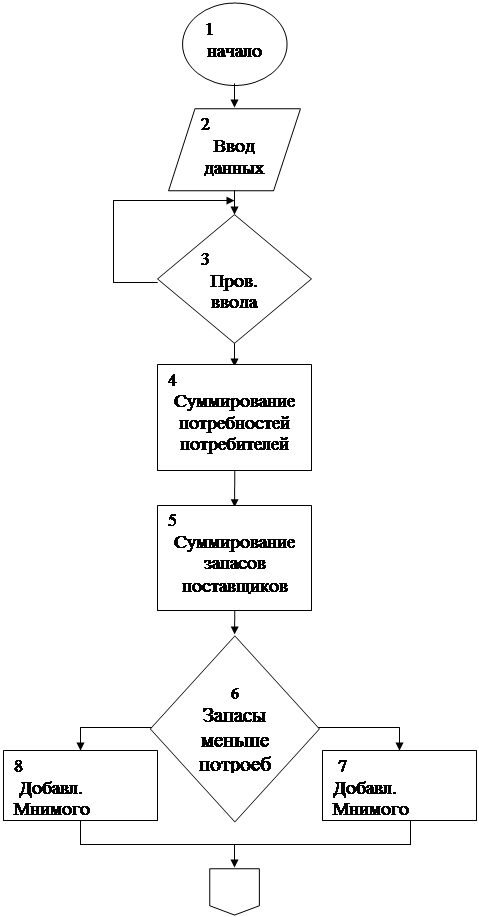
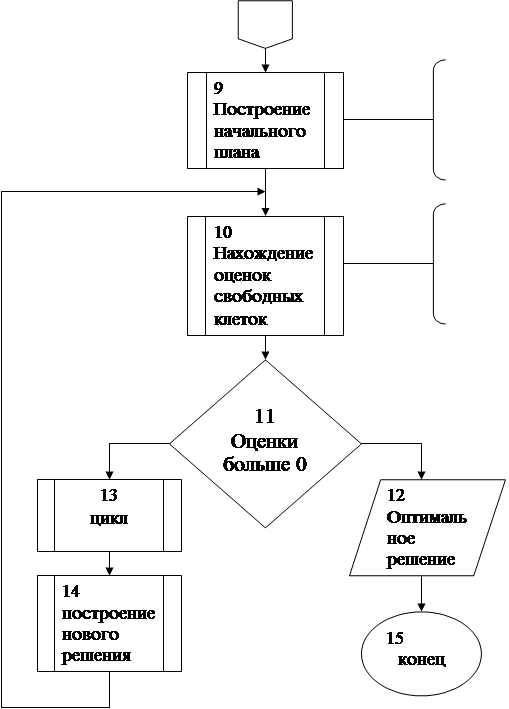
... . Система векторов условий транспортной задачи линейно независима тогда и только тогда, когда из соответствующих им клеток таблицы нельзя образовать ни одного цикла. Следовательно, допустимое решение транспортной задачи , i=1,2,…,m; j=1,2,…,n является опорным только в том случае, когда из занятых им клеток таблицы нельзя образовать ни одного цикла. Метод вычеркивания. Для проверки возможности ...
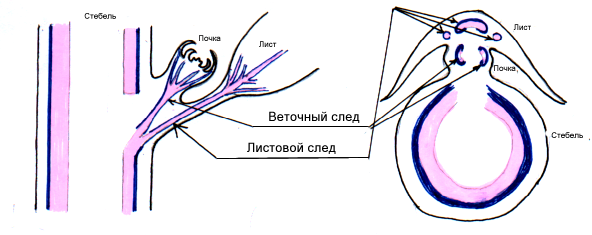
... , когда в три пучка листового следа объединяются при внедрении в лакуну центрального цилиндра. Полученные данные еще раз подтверждают ошибочность утверждения Шулькиной (1980) о том, что все представители семейства Campanulaceae обладают однолакунными однопучковыми узлами. Дальнейшие выводы можно стоить только определив строение узла у предков Campanulaceae. Если принять утверждение, что предок ...
... пользоваться и которая не подведет; - операционная система Windows XP Home Edition более удобная и более быстрая. 2. Разработка компьютерной сети на предприятии по разработке программного обеспечения 2.1 Постановка задачи Необходимо разработать локальную сеть из 70 компьютеров. Выбор технологии подключения к Интернет произволен. Удаленный участок сети необходимо разместить в диаметре 1 ...

0 комментариев