Навигация
3. Системы чёт-нечет
Рассмотрим систему
![]() (8)
(8)
Будем считать, что всюду в дальнейшем эта система удовлетворяет условиям:
а) Функция ![]() непрерывно дифференцируема, и поэтому, задача Коши для системы (8) имеет единственное решение;
непрерывно дифференцируема, и поэтому, задача Коши для системы (8) имеет единственное решение;
б) Правая часть системы (8) ![]() -периодична по
-периодична по ![]() .
.
Лемма 8 Пусть система (8) удовлетворяет условиям а) и б). Тогда продолжимое на отрезок ![]() решение
решение ![]() этой системы будет
этой системы будет ![]() -периодическим тогда и только тогда, когда
-периодическим тогда и только тогда, когда
![]()
где
![]()
– есть нечетная часть решения ![]() .
.
Доказательство. Пусть ![]() –
– ![]() -периодическое решение системы (8). Тогда
-периодическое решение системы (8). Тогда
![]()
Необходимость доказана.
Пусть ![]() – решение системы (8), для которого
– решение системы (8), для которого ![]() . Тогда
. Тогда
![]()
и поэтому
![]()
Таким образом, точка ![]() есть неподвижная точка отображения за период, а решение
есть неподвижная точка отображения за период, а решение ![]() –
– ![]() -периодическое.
-периодическое.
Доказанная лемма, вопрос о периодичности решения
![]()
сводит к вычислению одного из значений нечетной части ![]() . Иногда относительно
. Иногда относительно ![]() можно сказать больше, чем о самом решении
можно сказать больше, чем о самом решении ![]() . Это позволяет в таких случаях делать различные заключения относительно существования периодических решений у систем вида (8). Дифференцируемые функции
. Это позволяет в таких случаях делать различные заключения относительно существования периодических решений у систем вида (8). Дифференцируемые функции
![]()
![]()
удовлетворяют некоторой системе дифференциальных уравнений. Прежде, чем выписать эту систему, заметим:
![]() (9)
(9)
так как
![]()
решение системы (8). Заменяя в тождестве (9) ![]() на
на ![]() и учитывая, что производная четной функции – функция нечетная, а производная нечетной функции – функция четная, получаем тождество –
и учитывая, что производная четной функции – функция нечетная, а производная нечетной функции – функция четная, получаем тождество –
![]() (10)
(10)
Из тождеств (9) и (10) найдем производные:
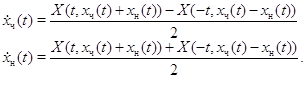
Таким образом вектор-функция
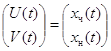 (11)
(11)
удовлетворяет следующей системе дифференциальных уравнений порядка ![]() :
:
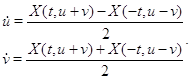 (12)
(12)
При этом
![]()
Систему (12) будем называть системой чет-нечет, соответствующей системе (8). решение системы чет-нечет, как следует из условия а), однозначно определяется своими начальными условиями.
4. Построение примеров систем, четная часть общего решения которых постоянная
Пример
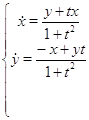
Найдем решение: будем использовать метод исключения, возьмем первое уравнение системы и выразим из него ![]() :
:
![]()
теперь продифференцируем его
![]()
Мы можем приравнять левую часть полученного уравнения с левой частью второго уравнения исходной системы
![]()
Сделаем преобразования и приведем подобные
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Таким образом:
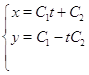
Сделаем проверку, для этого в исходную систему подставим полученное решение:
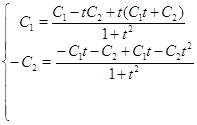
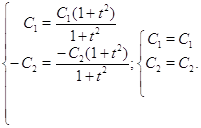
Получили верные равенства. Значит было найдено правильное решение исходной системы.
Четная часть общего решения:
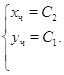
Пример
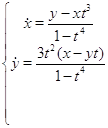
Найдем решение: будем использовать метод исключения, возьмем первое уравнение системы и выразим из него ![]() :
:
![]()
теперь продифференцируем его
![]()
Мы можем приравнять левую часть полученного уравнения с левой частью второго уравнения исходной системы
![]()
Сделаем преобразования и приведем подобные
![]()
![]()
![]()
![]()
![]()
![]()
Таким образом:
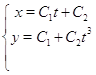
Сделаем проверку:
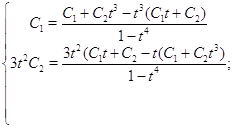
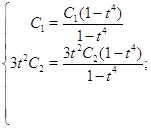
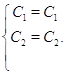
Четная часть общего решения
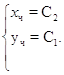
Пример
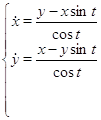
Найдем решение: будем использовать метод исключения, возьмем первое уравнение системы и выразим из него ![]() :
:
![]()
теперь продифференцируем его
![]()
Мы можем приравнять левую часть полученного уравнения с левой частью второго уравнения исходной системы
![]()
![]()
![]()
![]()
Получили два решения ![]() и
и ![]() .
.
1) ![]() ;
;
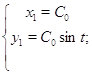
2) ![]() ;
;
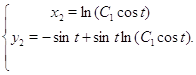
Сделаем проверку для ![]() :
:
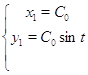
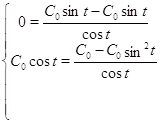
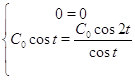
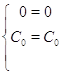
Получили верные равенства. Значит было найдено правильное решение исходной системы.
Сделаем проверку для ![]() :
:
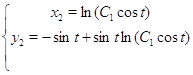

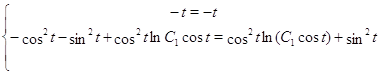
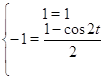
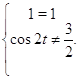
Отсюда видно, что ![]() не являются решением для исходной системы.
не являются решением для исходной системы.
Таким образом:
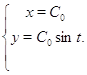
Четная часть общего решения
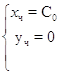
Из данных примеров можем заметить, что решения систем записывается в виде:
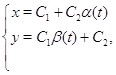
где ![]() и
и ![]() – нечетные функции, а четная часть представлена константой.
– нечетные функции, а четная часть представлена константой.
![]()
![]() ;
; ![]() ;
;
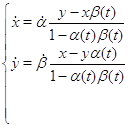 (13)
(13)
Системы вида (13) будут иметь семейства решений с постоянной четной частью. В этом легко убедится, проделав вычисления, аналогичные предыдущим примерам.
Похожие работы
... . Воспользуемся соотношением (1.4) (5.4) Таким образом, приходим к теореме: Теорема: Если система вида (5.1) имеет семейства решений с постоянной четной частью, то выполнено тождество (5.4) Заключение Мы исследовали понятие «отражающей функции». Для периодических решений дифференциальных систем и уравнений ...
... рисунков в формате А0-А1 со скоростью 10-30 мм/с. Фотонаборный аппарат Фотонаборный аппарат можно увидеть только в солидной полиграфической фирме. Он отличается своим высоким разрешением. Для обработки информации фотонаборный аппарат оборудуется процессором растрового изображения RIP, который функционирует как интерпретатор PostScript в растровое изображение. В отличие от лазерного принтера в ...
... от переподъемов, нулевую и максимальную защиты. - предусматривать остановку сосудов в промежуточных точках ствола. световую сигнализацию о режимах работы подъемной установки в здании подъемной машины, у оператора загрузочного устройства, у диспетчера. Современные регулируемые электроприводы постоянного тока для автоматизированных подъемных установок выполняют на основе двигателей постоянного ...
... . Реакции узлов более высокого уровня менее зависят от позиции и более устойчивы к искажениям. Структура Неокогнитрон имеет иерархическую структуру, ориентированную на моделирование зрительной системы человека. Он состоит из последовательности обрабатывающих слоев, организованных в иерархическую структуру (рис. 10.8). Входной образ подается на первый слой и передается через плоскости, ...
0 комментариев