Навигация
Построение множества систем, четная часть общего решения которых постоянна
6. Построение множества систем, четная часть общего решения которых постоянна
6.1 Системы, имеющие постоянную четную часть
Пусть нам дана система
![]() (14)
(14)
Перед нами стоит следующий вопрос о том, когда семейство решений этой системы будут иметь постоянную четную часть.
![]() (15)
(15)
То есть, когда ![]() не будет зависеть от времени
не будет зависеть от времени ![]() .
.
Возьмем отражающую функцию системы (14) ![]() и используя
и используя
![]()
получим четную часть следующим образом:
![]() (16)
(16)
Теорема 15 Если выполнено тождество
![]()
где ![]() – отражающая функция, для линейной системы вида (14), то любое решение этой системы имеет постоянную четную часть.
– отражающая функция, для линейной системы вида (14), то любое решение этой системы имеет постоянную четную часть.
Доказательство. Возьмем любое решение ![]() системы (14). Его производная
системы (14). Его производная
![]()
Поэтому можем записать
![]()
Из условия теоремы имеем
![]()
Таким образом получили, что ![]() – четная вектор-функция. Тогда
– четная вектор-функция. Тогда
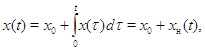
Рассмотрим систему (14). Будем строить систему с заданной четной частью.
Пусть нам известна четная часть ![]() . Воспользуемся формулой (15) и преобразуем ее
. Воспользуемся формулой (15) и преобразуем ее
![]()
Следовательно, можем записать
![]()
Отсюда зная (3), получим
![]()
где ![]() – отражающая функция системы. Исключая
– отражающая функция системы. Исключая ![]() из предыдущего соотношения, с произвольной отражающей функцией
из предыдущего соотношения, с произвольной отражающей функцией ![]() , удовлетворяющей условию
, удовлетворяющей условию
![]()
получим требуемую систему.
Пример 16 Пусть
![]()
где ![]() – заданная четная часть,
– заданная четная часть, ![]() . Продифференцируем обе части равенства
. Продифференцируем обе части равенства
![]()
Преобразуем правую часть
![]()
Перепишем полученное в виде:
![]()
Выразим ![]() :
:
![]() (17)
(17)
Для всех систем вида (17) должно быть выполнено условие
![]()
Возьмем
![]()
Найдем ![]() ,
, ![]() .
. ![]() ;
;
![]()
Подставим значения ![]() ,
, ![]() в систему (17):
в систему (17):
![]()
![]()
![]()
Получаем требуемую систему:
![]()
Пример 17 Пусть
![]()
где ![]() – заданная четная часть,
– заданная четная часть, ![]() . Продифференцируем обе части равенства
. Продифференцируем обе части равенства
![]()
и преобразуем правую часть
![]()
Перепишем полученное в виде:
![]()
Выразим ![]() :
:
![]() (18)
(18)
Для всех таких систем должно быть выполнено условие ![]() .
.
Возьмем ![]() . Найдем
. Найдем ![]() ,
, ![]() .
. ![]() ,
,
![]()
Подставим найденные значения в систему (18) и сделав преобразования аналогичные примеру 16, получаем:
![]()
Рассмотрим теперь общий случай, когда нам задана четная часть ![]() общего решения системы с отражающей функцией
общего решения системы с отражающей функцией ![]() . В этом случае
. В этом случае
![]()
Поэтому, если ![]() нам задана, то из соотношения
нам задана, то из соотношения
![]()
при заданной ![]() мы найдем общее решение
мы найдем общее решение ![]() искомой системы. Саму систему мы построим исключая
искомой системы. Саму систему мы построим исключая ![]() из соотношений
из соотношений
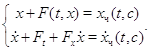
Таким образом, мы пришли к
Теорема 18 Всякая система
![]() (19)
(19)
где ![]() находятся из системы
находятся из системы
![]()
при любой заданной дифференцируемой функции ![]() , удовлетворяющей соотношениям
, удовлетворяющей соотношениям
![]()
имеет общее решение с четной частью ![]() .
.
Если
![]()
то система (19) имеет вид:
![]()
Таким образом, мы пришли к выводу:
Следствие 19 Общее решение дифференциальной системы имеет постоянную четную часть тогда и только тогда, когда эта система простейшая.
Заключение
Основным результатом данной работы является построение дифференциальных систем, семейство решений которых имеет заданную четную часть. А так же теорема о связи простейшей системы и системы, семейство решений которой имеет постоянную четную часть.
Теорема. Общее решение дифференциальной системы имеет постоянную четную часть тогда и только тогда, когда эта система простейшая.
Список использованных источников
[1] Арнольд В.И., Обыкновенные дифференциальные уравнения, М.: Наука, 1971 – 240 с.
[2] Бибиков Ю.Н., Общий курс дифференциальных уравнений, изд. Ленинградского университета, 1981 – 232 с.
[3] Еругин Н.П., Книга для чтения по общему курсу дифференциальных уравнений. 3-е издание, М. изд. Наука и Техника, 1979 – 744 с.
[4] Мироненко В.И., Отражающая функция и периодические решения дифференциальных уравнений, г. Минск: изд. Университетское, 1986 – 76 с.
[5] Понтрягин Л.С., Обыкновенные дифференциальные уравнения, М.: Наука, 1970 – 331 с.
Похожие работы
... . Воспользуемся соотношением (1.4) (5.4) Таким образом, приходим к теореме: Теорема: Если система вида (5.1) имеет семейства решений с постоянной четной частью, то выполнено тождество (5.4) Заключение Мы исследовали понятие «отражающей функции». Для периодических решений дифференциальных систем и уравнений ...
... рисунков в формате А0-А1 со скоростью 10-30 мм/с. Фотонаборный аппарат Фотонаборный аппарат можно увидеть только в солидной полиграфической фирме. Он отличается своим высоким разрешением. Для обработки информации фотонаборный аппарат оборудуется процессором растрового изображения RIP, который функционирует как интерпретатор PostScript в растровое изображение. В отличие от лазерного принтера в ...
... от переподъемов, нулевую и максимальную защиты. - предусматривать остановку сосудов в промежуточных точках ствола. световую сигнализацию о режимах работы подъемной установки в здании подъемной машины, у оператора загрузочного устройства, у диспетчера. Современные регулируемые электроприводы постоянного тока для автоматизированных подъемных установок выполняют на основе двигателей постоянного ...
... . Реакции узлов более высокого уровня менее зависят от позиции и более устойчивы к искажениям. Структура Неокогнитрон имеет иерархическую структуру, ориентированную на моделирование зрительной системы человека. Он состоит из последовательности обрабатывающих слоев, организованных в иерархическую структуру (рис. 10.8). Входной образ подается на первый слой и передается через плоскости, ...
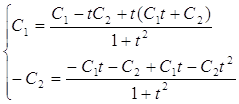
0 комментариев