Простые и простейшие системы

5. Простые и простейшие системы

Лемма 9 Для всякой непрерывно дифференцируемой функции

для которой выполнены тождества (4), имеют место соотношения

Теорема 10 Для всякой дважды непрерывно дифференцируемой функции  определенной в симметричной области , содержащей гиперплоскость  для которой выполнены тождества (4), существует дифференциальная система

c непрерывно дифференцируемой правой частью, отражающая функция которой совпадает с .

Теорема 11 Для всякой дважды непрерывно дифференцируемой функции

определенной в области  содержащей гиперплоскость , для которой выполнены тождества (4), при всех  и достаточно малых  существует дифференциальная система

отражающая функция которой совпадает с  а общий интеграл задается формулой

Следствие 12 Дважды непрерывно дифференцируемая функция

является отражающей функцией хотя бы одной дифференциальной системы тогда и только тогда, когда для нее выполнены тождества (4).

Системы, существование которых гарантируется теоремами 10 и 11, называются соответственно простой и простейшей.

Теорема 13 Пусть

простейшая система, тогда

где  – отражающая функция системы (1).

Доказательство. Если система простейшая,

Теорема 14 Пусть

есть отражающая функция некоторой дифференциальной системы, решения которой однозначно определяются своими начальными данными, а для непрерывно дифференцируемой функции

выполнены тождества (4). Тогда для того, чтобы в области  функция  совпадала с  необходимо и достаточно, чтобы рассматриваемая система имела вид

или вид

где

есть некоторая непрерывная вектор-функция.

Будем говорить, что множество систем вида (1) образует класс эквивалентности, если существует дифференцируемая функция

со свойствами:

1) Oтражающая функция

любой системы из рассматриваемого множества совпадает в своей области определения  с функцией

2) Любая система вида (1), отражающая функция

которой совпадает в области  с функцией  содержится в рассматриваемом множестве.

Две системы вида (1), принадлежащие одному классу эквивалентности, будем называть эквивалентными. Допуская определенную вольность речи, будем говорить также, что они имеют одну и ту же отражающую функцию. Функцию  при этом будем называть отражающей функцией класса, а класс – соответствующим отражающей функции .

Из третьего свойства отражающей функции следует, что система (1) и система

принадлежат одному классу эквивалентности тогда и только тогда, когда система уравнений

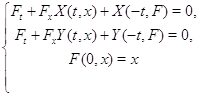
совместна.

Необходимым условием совместности этой системы является тождество .