Навигация
1 спосіб.
Нехай ![]() - точка перетину прямих, що містять бокові сторони
- точка перетину прямих, що містять бокові сторони ![]() і
і ![]() трапеції
трапеції ![]() ,
, ![]() - середина основи
- середина основи ![]() ,
, ![]() – точка перетину прямої
– точка перетину прямої ![]() з основою
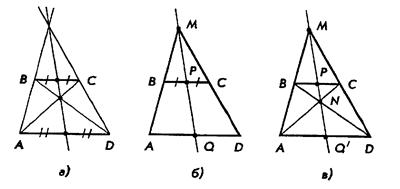
з основою ![]() (див. рис. б). Доведемо, що
(див. рис. б). Доведемо, що ![]() – середина відрізку
– середина відрізку ![]() , тобто точка
, тобто точка ![]() лежить на прямій, яка проходить через середини основ трапеції.
лежить на прямій, яка проходить через середини основ трапеції.
Оскільки трикутник ![]() подібний до трикутника
подібний до трикутника ![]() за першою ознакою подібності трикутників (
за першою ознакою подібності трикутників (![]() – спільний,
– спільний, ![]() ), то відношення
), то відношення
![]() . Аналогічно, трикутник
. Аналогічно, трикутник ![]() подібний до трикутника
подібний до трикутника ![]() , тому
, тому ![]() . З цих рівностей одержуємо, що
. З цих рівностей одержуємо, що ![]() . Так як
. Так як ![]() , то
, то ![]() , тобто
, тобто ![]() – середина основи
– середина основи ![]() .
.
Позначимо через ![]() точку перетину діагоналей
точку перетину діагоналей ![]() і
і ![]() , а через
, а через ![]() – точку перетину прямих
– точку перетину прямих ![]() і
і ![]() (див. рис. в). Аналогічно до попереднього, використовуючи подібність: трикутник
(див. рис. в). Аналогічно до попереднього, використовуючи подібність: трикутник ![]() подібний до трикутника
подібний до трикутника ![]() і трикутник
і трикутник ![]() подібний до трикутника
подібний до трикутника ![]() , доводиться, що
, доводиться, що ![]() – середина основи
– середина основи ![]() . Тобто точка
. Тобто точка ![]() лежить на прямій, що проходить через середини основ трапеції.
лежить на прямій, що проходить через середини основ трапеції.
2 спосіб.
Нехай ![]() задана трапеція з основами
задана трапеція з основами ![]() і
і ![]() . Застосуємо теорему Менелая до трикутника
. Застосуємо теорему Менелая до трикутника ![]() і трьом точкам
і трьом точкам ![]() (середина основи
(середина основи ![]() ),
), ![]() (точка перетину діагоналей
(точка перетину діагоналей ![]() і
і ![]() ),
), ![]() (точка перетину прямих
(точка перетину прямих ![]() і
і ![]() ) (див. рис. в).
) (див. рис. в).
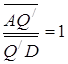 ,
, 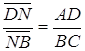 ,
, 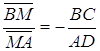 ,
,
так як трикутник ![]() подібний до трикутника
подібний до трикутника ![]() . Звідси випливає, що
. Звідси випливає, що
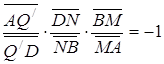 ,
,
тому точки ![]() лежать на одній прямій. Аналогічно доводиться, що середина
лежать на одній прямій. Аналогічно доводиться, що середина ![]() відрізка
відрізка ![]() лежить на прямій
лежить на прямій ![]() .
.
Задача 1.22 Через точку ![]() перетину діагоналей чотирикутника проведена січна. Відрізок цієї січної, що замкнений між однією парою протилежних сторін чотирикутника, поділяється точкою
перетину діагоналей чотирикутника проведена січна. Відрізок цієї січної, що замкнений між однією парою протилежних сторін чотирикутника, поділяється точкою ![]() навпіл. Довести, що відрізок січної, що замкнений між продовженнями іншої пари протилежних сторін чотирикутника поділяється точкою
навпіл. Довести, що відрізок січної, що замкнений між продовженнями іншої пари протилежних сторін чотирикутника поділяється точкою ![]() також навпіл.
також навпіл.
Доведення.
Нехай січна ![]() зустрічає сторони
зустрічає сторони ![]() і
і ![]() чотирикутника
чотирикутника ![]() в точках
в точках ![]() і
і ![]() , а продовження сторін
, а продовження сторін ![]() і
і ![]() – в точках
– в точках ![]() і
і ![]() . Тоді скориставшись теоремою Менелая для трикутників
. Тоді скориставшись теоремою Менелая для трикутників ![]() і
і ![]() , які перетинаються прямими
, які перетинаються прямими ![]() і
і ![]() , одержуємо, що
, одержуємо, що
![]() і
і ![]() .
.
Тоді
![]() .
.
Але за умовою ![]() , і для чотирикутника
, і для чотирикутника ![]() і січної
і січної ![]() згідно з теоремою Менелая маємо
згідно з теоремою Менелая маємо
![]() .
.
Отже, ![]() або
або ![]() . Звідси
. Звідси ![]() і
і ![]() .
.
РОЗДІЛ 2
ТЕОРЕМА МЕНЕЛАЯ ДЛЯ ДОВІЛЬНОГО ТЕТРАЕДРА
Досить ефективно при розв’язанні деяких задач застосовується мало відома стереометрична теорема Менелая для довільного тетраедра.
Теорема Менелая для тетраедра. У довільному тетраедрі ![]() точки
точки
![]() належать ребрам
належать ребрам ![]() і
і ![]() відповідно (див. рис. 2.1). Для того, щоб точки
відповідно (див. рис. 2.1). Для того, щоб точки ![]() належали однієї площині, необхідно і достатньо, щоб виконувалось співвідношення
належали однієї площині, необхідно і достатньо, щоб виконувалось співвідношення
![]() (2.1)
(2.1)

Рис 2.1 До формулювання теореми Менелая для довільного тетраедра
Доведення. Необхідність. Нехай чотирикутник ![]() – перетин даного тетраедра деякою площиною
– перетин даного тетраедра деякою площиною ![]() . Проведемо
. Проведемо ![]() – перпендикуляри до площи-ни
– перпендикуляри до площи-ни ![]() . Розглянемо «фрагмент» – перетин ребра
. Розглянемо «фрагмент» – перетин ребра ![]() площиною
площиною ![]() (див. рис. 2.2).
(див. рис. 2.2).
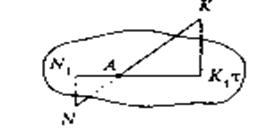
Рис 2.2 До доведення теореми Менелая
Трикутники ![]() та
та ![]() подібні, тому
подібні, тому 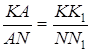 .
.
Трикутники ![]() та
та ![]() подібні, тому
подібні, тому 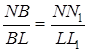 .
.
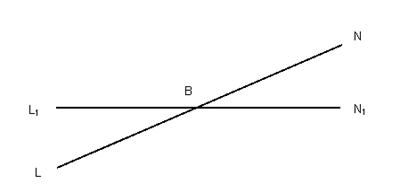
Трикутники ![]() та
та ![]() подібні, тому
подібні, тому 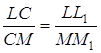 .
.
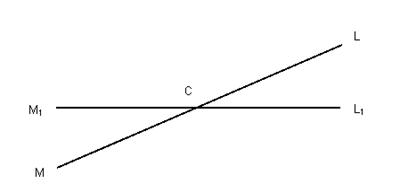
Трикутники ![]() та
та ![]() подібні, тому
подібні, тому 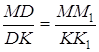 .
.
Перемножуючи знайдені пропорції, приходимо до рівності:
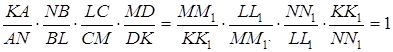 .
.
Достатність. Припустимо, що виконується співвідношення (2.1), але точки ![]() не лежать в одній площині. Проведемо через точки
не лежать в одній площині. Проведемо через точки ![]() площину
площину ![]() , що перетинає ребро
, що перетинає ребро ![]() в деякій точці
в деякій точці ![]() , відмінної від
, відмінної від ![]() . Тому
. Тому 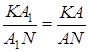 ,
,
отже, співвідношення (2.1) для точок ![]() виконуватися не буде. Оскільки ми прийшли до протиріччя з вихідною умовою (не виконується рівність (2.1)), то наше припущення невірне й площина
виконуватися не буде. Оскільки ми прийшли до протиріччя з вихідною умовою (не виконується рівність (2.1)), то наше припущення невірне й площина ![]() пройде через точку
пройде через точку ![]() .
.
Теорема доведена.
Наведемо застосування цієї теореми до розв’язання стереометричних задач.
Задача 2.1 У тетраедрі ![]() точки
точки ![]() належать ребрам
належать ребрам ![]() і
і ![]() відповідно (див. рис. 2.3), причому
відповідно (див. рис. 2.3), причому ![]() і
і ![]() . Через точки
. Через точки ![]() проведена площина
проведена площина ![]() . У якому відношенні ця площина поділяє об’єм тетраедра?
. У якому відношенні ця площина поділяє об’єм тетраедра?
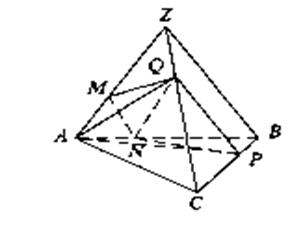
Рис. 2.3 До задачі 2.1
Розв’язок. Нехай площина ![]() перетинає ребро
перетинає ребро ![]() в точці
в точці ![]() . Чотирикутник
. Чотирикутник ![]() – переріз даного тетраедра площиною
– переріз даного тетраедра площиною ![]() . Визначимо, у якому відношенні точка
. Визначимо, у якому відношенні точка ![]() поділяє ребро
поділяє ребро ![]() . На підставі співвідношення (2.1) та умови задачі маємо
. На підставі співвідношення (2.1) та умови задачі маємо
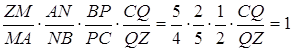 ,
,
звідки ![]() .
.
У багатограннику
![]() проведемо переріз через ребро
проведемо переріз через ребро ![]() і вершину
і вершину ![]() . Цей переріз розбиває розглянутий багатогранник на трикутну піраміду
. Цей переріз розбиває розглянутий багатогранник на трикутну піраміду ![]() і чотирикутну піраміду
і чотирикутну піраміду ![]() , яка
діагональним перерізом
, яка
діагональним перерізом ![]() розбивається на дві трикутні піраміди:
розбивається на дві трикутні піраміди: ![]() .
.
Нехай ![]() – площа грані
– площа грані ![]() ,
, ![]() – довжина висоти тетраедра, проведена з вершини
– довжина висоти тетраедра, проведена з вершини ![]() ,
, ![]() – об’єм даного тетраедра. Визначимо об’єми трьох отриманих вище трикутних пірамід. Для піраміди
– об’єм даного тетраедра. Визначимо об’єми трьох отриманих вище трикутних пірамід. Для піраміди ![]() :
:
![]()
де ![]() – довжина висоти трикутної піраміди
– довжина висоти трикутної піраміди ![]() , проведена з вершини
, проведена з вершини ![]() на площину грані
на площину грані ![]() (
(![]() ). Тоді
). Тоді
![]()
![]()
Нехай далі ![]() – площа грані
– площа грані ![]() ,
, ![]() – довжина висоти даного тетраедра, проведена з вершини
– довжина висоти даного тетраедра, проведена з вершини ![]() на площину грані
на площину грані ![]() . Тоді
. Тоді
![]()
де ![]() – довжина перпендикуляра, проведеного з вершини
– довжина перпендикуляра, проведеного з вершини ![]() на площину грані
на площину грані ![]() (
(![]() ) і
) і
![]()
Знайдемо тепер об’єм багатогранника ![]() :
:
![]()
Отже, ![]() .
.
У такий спосіб шукане відношення дорівнює 23:40.
Відповідь: 23:40.
Задача 2.2. Об’єм тетраедра ![]() дорівнює 5. Через середини ребер
дорівнює 5. Через середини ребер ![]() проведена площина, яка перетинає ребро
проведена площина, яка перетинає ребро ![]() в точці
в точці ![]() . При цьому відношення довжини відрізка
. При цьому відношення довжини відрізка ![]() до довжини відрізка
до довжини відрізка ![]() дорівнює
дорівнює ![]() . Знайдіть площу перерізу тетраедра зазначеною площиною, якщо відстань до неї від вершини
. Знайдіть площу перерізу тетраедра зазначеною площиною, якщо відстань до неї від вершини ![]() дорівнює 1.
дорівнює 1.
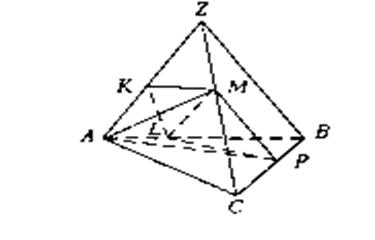
Рис. 2.4 До задачі 2.2
Розв’язок.
Нехай ![]() і
і ![]() – середини ребер
– середини ребер ![]() відповідно і
відповідно і ![]() .
.
Чотирикутник ![]() – заданий за умовою переріз. На підставі теореми Менелая
– заданий за умовою переріз. На підставі теореми Менелая
![]() ,
,
![]() ,
,
звідки ![]() .
.
З'єднаємо точки ![]() і
і ![]() ,
, ![]() і
і ![]() ,
, ![]() і
і ![]() .
.
Нехай ![]() і довжина висоти тетраедра, проведена з вершини
і довжина висоти тетраедра, проведена з вершини ![]() На рисунку не наведено), дорівнює
На рисунку не наведено), дорівнює ![]() . Згідно з умовою задачі
. Згідно з умовою задачі ![]() . Висота
піраміди
. Висота
піраміди ![]() , проведена з вершини
, проведена з вершини ![]() дорівнює
дорівнює ![]() .
.
Знайдемо тепер об’єм піраміди ![]() :
:
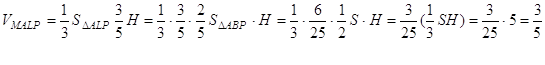
Далі нехай ![]() і довжина висоти тетраедра, проведена з вершини
і довжина висоти тетраедра, проведена з вершини ![]() на грань
на грань ![]() дорівнює
дорівнює ![]() . Тоді об’єм піраміди
. Тоді об’єм піраміди ![]() дорівнює
дорівнює
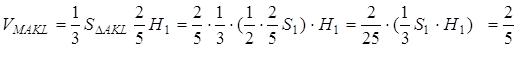
![]() .
.
З іншої сторони (враховуючи, що відстань від вершини ![]() до площини перерізу за умовою задачі дорівнює 1), маємо
до площини перерізу за умовою задачі дорівнює 1), маємо
![]()
Отже, ![]() .
.
Відповідь: 3.
Задача 2.3 В піраміді ![]() проведений переріз
проведений переріз ![]() так, що точка
так, що точка ![]() лежить на ребрі
лежить на ребрі ![]() точка
точка ![]() – на ребрі
– на ребрі ![]() , точка
, точка ![]() – на ребрі
– на ребрі ![]() , точка
, точка ![]() – на ребрі
– на ребрі ![]() . Відомо, що
. Відомо, що ![]() ,
, ![]() .
.
Знайти відношення об’ємів частин, на які площина ![]() поділяє піраміду.
поділяє піраміду.
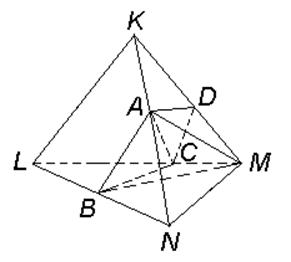
Рис 2.5 До задачі 2.3
Розв’язок.
З умови задачі безпосередньо випливає, що
![]() (2.3.1)
(2.3.1)
![]() (2.3.2)
(2.3.2)
Нехай ![]() ,
, ![]() .
.
Згідно з теоремою Менелая маємо
![]()
Враховуючи (2.3.1) і (2.3.2) й прийняті вище позначення одержуємо
![]() ,
,
звідки ![]() (2.3.3)
(2.3.3)
Розділивши обидві частини останньої рівності з умови задачі на ![]() , одержуємо
, одержуємо
![]()
або
![]() (2.3.4)
(2.3.4)
З (2.3.3) і (2.3.4) складаємо систему
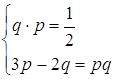
Розв’язуємо цю систему:
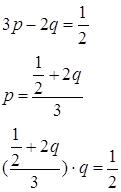
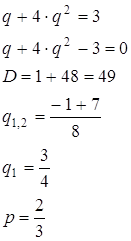
![]() і
і ![]()
Розбиваємо багатогранник ![]() на три трикутні піраміди:
на три трикутні піраміди: ![]() ,
, ![]() .
.
Нехай ![]() – площа трикутника
– площа трикутника ![]() ,
, ![]() – довжина висоти даної піраміди, проведена з вершини
– довжина висоти даної піраміди, проведена з вершини ![]() ,
, ![]() – об’єм даної піраміди,
– об’єм даної піраміди, ![]() – довжина висоти піраміди
– довжина висоти піраміди ![]() , проведена з вершини
, проведена з вершини ![]() . Тоді маємо
. Тоді маємо
![]()
![]()
Нехай ![]() – площа грані
– площа грані ![]() ,
, ![]() – довжина висоти даної піраміди, проведена з вершини
– довжина висоти даної піраміди, проведена з вершини ![]() на площину грані
на площину грані ![]() ,
, ![]() – довжина перпендикуляра, опущеного з точки
– довжина перпендикуляра, опущеного з точки ![]() на площину грані
на площину грані ![]() . Тоді маємо
. Тоді маємо
![]()
Знайдемо об’єм багатогранника ![]() :
:
![]()
Отже, ![]() .
.
Таким чином, шукане відношення дорівнює 17:18.
Відповідь: 17:18.
Задача 2.4 Задана піраміда ![]() , основа якої має форму опуклого чотирикутни-ка
, основа якої має форму опуклого чотирикутни-ка ![]() зі взаємно перпендикулярними діагоналями
зі взаємно перпендикулярними діагоналями ![]() і
і ![]() . Основа перпендикуляра, опущеного з вершини
. Основа перпендикуляра, опущеного з вершини ![]() на основу піраміди, збігається з точкою
на основу піраміди, збігається з точкою ![]() – перетином діагоналей
– перетином діагоналей ![]() і
і ![]() . Довести, що основи перпендикулярів, опущених із точки
. Довести, що основи перпендикулярів, опущених із точки ![]() на бічні грані піраміди, лежать на одному колі.
на бічні грані піраміди, лежать на одному колі.
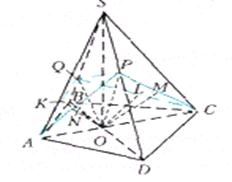
Рис. 2.6 До задачі 2.4
Розв’язок.
Нехай ![]() – перпендикуляр до площини
– перпендикуляр до площини ![]() ,
, ![]() – перпендикуляр до площини
– перпендикуляр до площини ![]() ,
, ![]() – перпендикуляр до площини
– перпендикуляр до площини ![]() . Покажемо, наприклад, що точка
. Покажемо, наприклад, що точка ![]() – ортоцентр грані
– ортоцентр грані ![]() . В площині грані
. В площині грані ![]() проведемо промінь
проведемо промінь ![]() до перетину з ребром
до перетину з ребром ![]() в точці
в точці ![]() . Згідно з умовою,
. Згідно з умовою, ![]() і
і ![]() . Тому
. Тому ![]() .
.
Згідно з теоремою про три перпендикуляри (![]() ,
, ![]() – похила,
– похила, ![]() –її проекція на
–її проекція на ![]() ) маємо, що
) маємо, що ![]() . Аналогічно доводиться, що
. Аналогічно доводиться, що ![]() . Отже, точка
. Отже, точка ![]() – ортоцентр грані
– ортоцентр грані ![]() .
.
Аналогічно доводиться, що точки ![]() і
і ![]() також є ортоцентрами відповідних граней.
також є ортоцентрами відповідних граней.
З'єднаємо точки ![]() і
і ![]() . Згідно з теоремою про три перпендикуляри
. Згідно з теоремою про три перпендикуляри ![]() . З'єднаємо точки
. З'єднаємо точки ![]() і
і ![]() . Згідно з теоремою про три перпендикуляри
. Згідно з теоремою про три перпендикуляри ![]() .
.
Оскільки з точки ![]() в грані
в грані ![]() на
на ![]() можна провести тільки один перпендикуляр, то відрізок
можна провести тільки один перпендикуляр, то відрізок ![]() пройде через точку
пройде через точку ![]() . Отже, висоти, проведені в гранях
. Отже, висоти, проведені в гранях ![]() і
і ![]() з вершин
з вершин ![]() і
і ![]() на ребро
на ребро ![]() , проходять через точки
, проходять через точки ![]() і
і ![]() відповідно і перетинають ребро
відповідно і перетинають ребро ![]() в точці
в точці ![]() .
.
Аналогічно доводиться, що висоти граней ![]() і
і ![]() , проведені з вершин
, проведені з вершин ![]() і
і ![]() на ребро
на ребро ![]() , проходять через точки
, проходять через точки ![]() і
і ![]() відповідно і попадають в ту саму точку
відповідно і попадають в ту саму точку ![]() на ребрі
на ребрі ![]() .
.
Розглянемо трикутник ![]() , у якому
, у якому ![]() і
і ![]() (див. рис 2.7)
(див. рис 2.7)
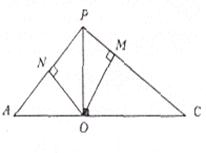
Рис 2.7
Нехай ![]() і
і ![]() . Тоді
. Тоді ![]() і
і ![]() .
.
З ![]() :
:
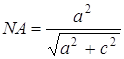 ;
; 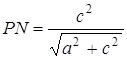 ;
; 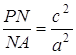 .
.
З ![]() :
:
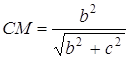 ;
; 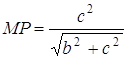 ;
; 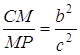 .
.
Аналогічно розглянемо ![]() , нехай
, нехай ![]() (див. рис. 2.8).
(див. рис. 2.8).
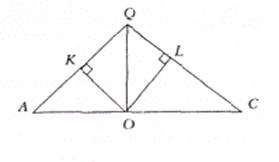
Рис 2.8
З ![]()
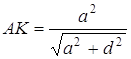 ;
; 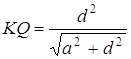 ;
; 
З ![]()
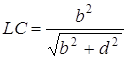 ;
; 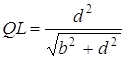 ;
; 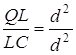
Точки ![]() і
і ![]() належать відповідно ребрам
належать відповідно ребрам ![]() і
і ![]() тетраедра
тетраедра ![]() . Розглянемо добуток
. Розглянемо добуток
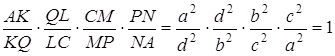
З того, що розглянутий добуток дорівнює 1, випливає, що точки ![]() і
і ![]() належать однієї площини (назвемо неї
належать однієї площини (назвемо неї ![]() ). Побудуємо на
). Побудуємо на ![]() , як на діаметрі сферу (на рисунку не наведено). Оскільки
, як на діаметрі сферу (на рисунку не наведено). Оскільки ![]() , то вершини цих кутів лежать на побудованій сфері. А так як точки
, то вершини цих кутів лежать на побудованій сфері. А так як точки ![]() і
і ![]() належать також площині
належать також площині ![]() , то ці точки лежать на перетині площини
, то ці точки лежать на перетині площини ![]() зі сферою тобто на колі.
зі сферою тобто на колі.
Задача 2.5 В тетраедрі ![]() через середини
через середини ![]() та
та ![]() ребер
ребер ![]() та
та ![]() проведена площина, яка перетинає ребра
проведена площина, яка перетинає ребра ![]() та
та ![]() відповідно в точках
відповідно в точках ![]() та
та ![]() . Площа чотирикутника
. Площа чотирикутника ![]() дорівнює 16, а відношення довжини відрізка
дорівнює 16, а відношення довжини відрізка ![]() до довжини відрізка
до довжини відрізка ![]() дорівнює 0,5. Обчислити
відстань від вершини
дорівнює 0,5. Обчислити
відстань від вершини ![]() до площини
до площини ![]() , якщо об’єм багатогранника
, якщо об’єм багатогранника ![]() дорівнює 8.
дорівнює 8.
Розв’язок.
Згідно з теоремою Менелая для тетраедра![]() ,
,
![]() ,
, ![]() .
.
Знайдемо об’єм ![]() :
:
![]()
Знаходимо ![]() , де
, де ![]() - площа
- площа ![]() ,
, ![]() - висота
- висота ![]() проведена з вершини
проведена з вершини ![]() ,
, ![]() - об’єм
- об’єм ![]() .
.
Знаходимо висоту ![]() :
:
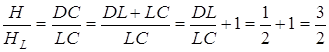
![]()
![]()
Знаходимо площу ![]() .
.
![]() ,
, ![]()
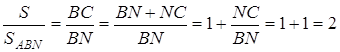
![]() ,
, ![]()
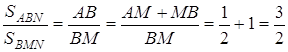
![]()
Тоді ![]()
![]()
![]()
Знайдемо об’єм ![]()
![]() ,
,
де ![]() - висота, проведена з вершини
- висота, проведена з вершини ![]() до
до ![]() ,
, ![]() - висота проведена з вершини
- висота проведена з вершини ![]() до
до ![]() .
.
Знаходимо висоту ![]() :
:
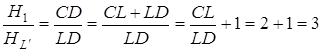
![]()
Знаходимо площу ![]() .
.
![]() ,
, ![]()
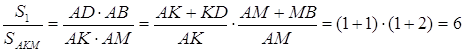
![]()
Тоді ![]()
Отже, ![]()
Тоді ![]()
![]()
Залишилось знайти ![]()
![]() ,
,
де ![]() .
.
Знайдемо площу ![]() .
.
![]() ,
, ![]()
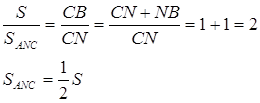
Тоді ![]()
Отже
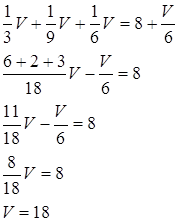
Знаходимо відстань від вершини ![]() до площини
до площини ![]()
![]()
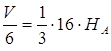
![]()
Відповідь: ![]() .
.
Задача 2.6 В тетраедрі ![]() проведено переріз
проведено переріз ![]() так, що точка
так, що точка ![]() лежить на ребрі
лежить на ребрі ![]() , точка
, точка ![]() – на ребрі
– на ребрі ![]() , точка
, точка ![]() – на ребрі
– на ребрі ![]() , точка
, точка ![]() - на ребрі
- на ребрі ![]() . Переріз
. Переріз ![]() ділить піраміду на дві частини. Знайти відношення об’ємів цих частин, якщо відомі наступні співвідношення між довжинами відрізків
ділить піраміду на дві частини. Знайти відношення об’ємів цих частин, якщо відомі наступні співвідношення між довжинами відрізків
![]() та
та ![]() .
.
Розв’язок.
Нам треба знайти 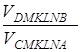 .
.
Нехай ![]() , відомо
, відомо ![]() .
.
Згідно з теоремою Менелая для тетраедра
![]() ,
,
![]() ,
, ![]() .
.
З умови задачі маємо
![]()
![]()
![]()
![]()
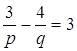
![]()
Складаємо систему : 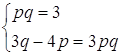
![]()

Отже, ![]() .
.
Розбиваємо багатогранник ![]() на три трикутні піраміди:
на три трикутні піраміди:
![]() .
.
Знайдемо об’єм піраміди ![]() . Нехай
. Нехай ![]() – площа трикутника
– площа трикутника ![]() ,
, ![]() – довжина висоти даної піраміди, проведена з вершини
– довжина висоти даної піраміди, проведена з вершини ![]() ,
, ![]() – об’єм піраміди
– об’єм піраміди ![]() ,
, ![]() –довжина висоти піраміди
–довжина висоти піраміди ![]() .
.
Тоді
![]()
Знайдемо ![]() та
та ![]() .
.
![]() ,
, ![]()
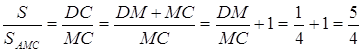
![]()
![]()
Знайдемо висоту
![]() :
: 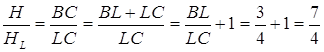
![]()
![]()
Отже, ![]()
Знайдемо об’єм піраміди ![]() :
:
![]()
Відомо, що ![]() . Знайдемо
. Знайдемо ![]() .
.
![]() ,
, ![]()
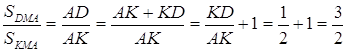
Відомо, що ![]()
![]()
![]()
Отже,
![]()
Знайдемо об’єм піраміди ![]() . Нехай
. Нехай ![]() - площа грані
- площа грані ![]() ,
, ![]() – довжина висоти даної піраміди проведена з вершини
– довжина висоти даної піраміди проведена з вершини ![]() на площину грані
на площину грані ![]() ,
, ![]() –довжина перпендикуляра, опущеного з точки
–довжина перпендикуляра, опущеного з точки ![]() на площину грані
на площину грані ![]() .
.
Тоді
![]()
Знайдемо ![]() та
та ![]()
![]() ,
, ![]()
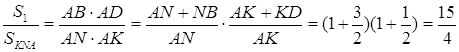
![]()
![]()
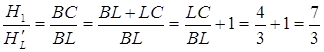
![]()
![]()
Отже, ![]()
Об’єм багатогранника
![]() .
.
Отже, ![]() .
.
Остаточно 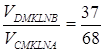
Відповідь: 37:68.
Задача 2.7 Точки ![]() не належать одній площині. Відрізки
не належать одній площині. Відрізки ![]() і
і ![]() поділені точками
поділені точками ![]() та
та ![]() так, що
так, що ![]() , а відрізки
, а відрізки ![]() і
і ![]() поділені точками
поділені точками ![]() та
та ![]() так, що
так, що 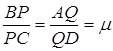 . Довести, що точки
. Довести, що точки ![]() та
та ![]() належать одній площині.
належать одній площині.
Доведення.
Розглянемо добуток 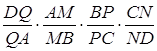 . Підставляємо відомі відношення з умови
. Підставляємо відомі відношення з умови
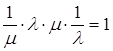
Це і є необхідна й достатня умова належності точок ![]() та
та ![]() одній площині.
одній площині.
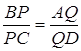 .
. Доведення.
За умовою задачі ![]() . Згідно з теоремою Менелая для тетраедра
. Згідно з теоремою Менелая для тетраедра
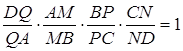
 ,
, 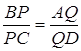 .
.
Задача 2.9 Сфера дотикається сторін ![]() просторового чотирикутника в точках
просторового чотирикутника в точках ![]() відповідно. Довести, що точки
відповідно. Довести, що точки ![]() лежать в одній площині.
лежать в одній площині.
Доведення.
З рівності відрізків дотичних випливає, що
![]()
Проведемо площину через точки ![]() . Нехай вона перетинає
. Нехай вона перетинає ![]() в точці
в точці ![]() . Тоді
. Тоді
![]() .
.
Знаходимо, що ![]() , але тоді
, але тоді ![]() . Отже, точки
. Отже, точки ![]() лежать в одній площині.
лежать в одній площині.
РОЗДІЛ 3
ТЕОРЕМИ ЧЕВИ ДЛЯ ТРИКУТНИКА ТА ТЕТРАЕДРА.ТЕОРЕМА ЧЕВИ В ФОРМІ СИНУСІВ
0 комментариев