Застосування теорем Чеви для розв’язання задач

3.2 Застосування теорем Чеви для розв’язання задач

Задача 3.1. Задано трикутник АВС. Як слід побудувати точку О всередині трикутника, щоб площі трикутників АОС, ВОС та АОВ відносилися як 7 : 11 : 13.

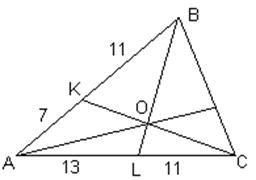
Розв’язок.

1 спосіб.

Розглянемо трикутник АВС й побудуємо точку K, яка ділить сторону AB у відношенні 7 : 11, рахууючи від вершини A, та точку L, яка ділить сторону CA у відношенні 11 : 13, рахууючи від вершини C.

Нехай O – точка перетину відрізків CK та BL. Покажемо, що O – шукана точка. Зазначимо, що у трикутників ACK та BCK спільна висота, яка опущена з вершини С, тому відношення їх площин дорівнює відношенню основ

S_ACK : S_BCK = AK : BK.

Аналогічно, S_AOK : S_BOK = AK : BK.

Застосовуючи властивість пропорції ( Û ), одержуємо

S_AOС : S_BOС = AK : BK = 7 : 11.

Аналогічно, розглядаючи дві пари трикутників з основами AL та СL, доводимо, що

S_BOС : S_AOВ = CL : AL = 11 : 13.

Отже, S_AOС : S_BOС : S_AOВ = 7 : 11 : 13, що і необхідно було довести.

2 спосіб.

З теореми Чеви випливає, що пряма АO розділить сторону ВС у відношенні 13 : 7, рахууючи від вершини В. Якщо застосовувати теорему Чеви в обернену сторону, то до розв’язку задачі можна було підійти інакше.

Нехай задано відрізок PQ, точка E, яка ділить його у відношенні p : q, де p та q – задані числа, й точка F, яка не належить прямій PQ. Аналогічно з наведеним розв’язком можна довести, що геометричним місцем точок М площини, для яких S_PFM : S_QFM = p : q є пряма EF (за виключенням точок E та F).

Отже, для того, щоб побудувати шукану точку О можна розділити сторони АВ, ВС та СА трикутника АВС відповідно точками K, N та L так, щоб

AK : BK = 7 : 11; BN : CN = 13 : 7; CL : AL = 11 : 13.

Тоді, згідно з теоремою Чеви , отже, відрізки AN, BL та CK перетинаються в одній точці, яка й буде шуканою.

Задача 3.2. В трикутник  вписано півколо так, що його діаметр лежить на стороні , а дуга дотикається сторін  та відповідно в точках  та . Довести, що прямі  та  перетинаються на висоті  трикутника.

Доведення.

З умови задачі випливає, що точки  та  лежать на сторонах трикутника . Отже, достатньо довести, що

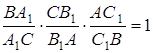
Центр  півкола з'єднаємо з точками дотику  та  (див. рисунок). Позначимо через радіус кола, з прямокутних трикутників  та  знаходимо

.

З прямокутних трикутників та  маємо

.

Зазначимо, що відрізки  та дотичних до кола рівні, отже отримаємо

.

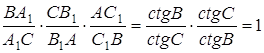Отже, згідно з теоремою Чеви прямі  та  перетинаються в одній точці.

 

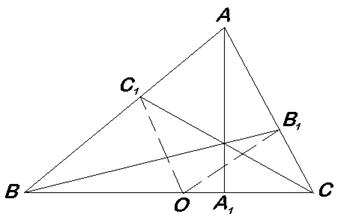
Задача 3.3. Через вершини трикутника і точку , яка лежить всередині трикутника, проведені прямі, що перетинають сторони відповідно в точках , при цьому .

Довести, що 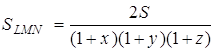 , де – площа трикутника .

Як належить обрати точку , щоб площа трикутника  була найбільшою?

Розв’язок.

Позначимо площі трикутників ,  через .

Так як площі двох трикутників, які мають спільний кут, відносяться як добуток сторін, що утворюють цей кут, то

.

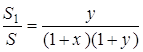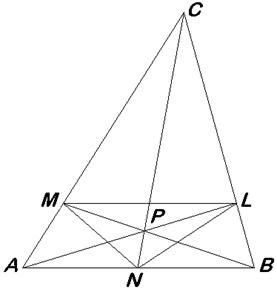
Аналогічно , .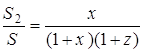

Далі знаходимо

.

Підставив в цю рівність знайдені вище значення та прийняв до уваги, що в силу теореми Чеви , одержуємо:

.

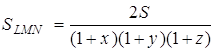Площа трикутника буде найбільшою при мінімальному значенні . Проведемо оцінку цього добутку.

Скористаємося нерівністю нерівність :

,

при цьому рівність має місце тоді й тільки тоді, коли .

Отже, шукана точка  – точка перетину медіан трикутника , для якої .

Задача 3.4. Знайти в трикутнику таку точку , щоб добуток  мав найбільшу величину ( – точки перетину прямих  зі сторонами ).

Розв’язок.

Проведемо медіани  трикутника , які перетинаються в точці . Оскільки середнє геометричне двох величин не більше їх середнього арифметичного, то

, , .

Піднесемо кожну нерівність до квадрата та перемножимо:

Згідно з теоремою Чеви маємо

.

Отже,

.

Нерівність перетворюється в рівність у випадку збігу основ прямих Чеви з серединами відповідних сторін, отже, в цьому випадку добуток  має найбільшу величину , де – сторони трикутника.Отже, шуканою точкою є точка перетину медіан трикутника.

Задача 3.5. Прямі  перетинають сторони трикутника  (або їхні продовження) у точках . Довести, що:

а) прямі, що проходять через середини сторін  паралельно прямим , перетинаються в одній точці;

б) прямі, що з'єднують середини сторін  із серединами відрізків , перетинаються в одній точці.

Доведення.

Нехай  – середини сторін . Розглянуті прямі проходять через вершини трикутника , при цьому в задачі а) вони ділять його сторони в таких же відношеннях, у яких прямі  ділять сторони трикутника , а в задачі б) – вони ділять їх у зворотних відношеннях. Залишається скористатись теоремою Чеви.

Задача 3.6. На сторонах  трикутника  взяті точки  так, що відрізки  перетинаються в одній точці. Прямі  і  перетинають пряму, що проходить через вершину  паралельно стороні , в точках  і  відповідно. Довести, що .

Доведення.

Оскільки  і , то

Тому

 

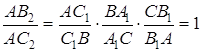
Задача 3.7. а) Нехай  – довільні кути, при цьому сума будь-яких двох з них менше 180. На сторонах трикутника  зовнішнім чином побудовані трикутники , що мають при вершинах  кути . Довести, що прямі  перетинаються в одній точці.

б) довести аналогічне твердження для трикутників, побудованих на сторонах трикутника  внутрішнім чином.

Доведення.

Нехай прямі  перетинають прямі в точках .

Якщо  і , то

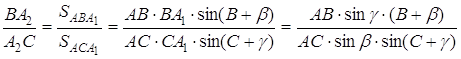
Останній вираз дорівнює  у всіх випадках.

Аналогічно записуються вирази для  і . Перемножуємо всі вирази і залишається скористатися теоремою Чеви.

Задача 3.8. Прямі  перетинають прямі  в точках  відповідно. Точки  обрані на прямих  так, що

, , .

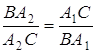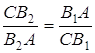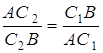Довести, що прямі  також перетинаються в одній точці  (або паралельні). Такі точці  і  називають ізотомічно спряженими відносно трикутника .

Доведення очевидним чином випливає з теореми Чеви.

Задача 3.9. На сторонах  трикутника  взяті точки , при цьому прямі  перетинаються в одній точці . Довести, що прямі

 симетричні цим прямим відносно відповідних бісектрис, також перетинаються в одній точці . Такі точки  і  називають ізогонально спряженими відносно трикутника .

Доведення.

Можна вважати, що точки  лежать на сторонах трикутника .

Згідно з теоремою Чеви в формі синусів

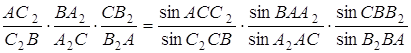
Оскільки прямі  симетричні прямим  відносно бісектрис, то ,  і т.д., тому

Отже,

,

тобто прямі  перетинаються в одній точці.

Задачі для самостійної роботи

Задача 3.10. Протилежні сторони опуклого шестикутника попарно паралельні. Довести, що прямі, які з'єднують середини протилежних сторін, перетинаються в одній точці.

Доведення

Нехай діагоналі  і  даного шестикутника  перетинаються в точці ;  і  – середини сторін  і . Оскільки  - трапеція, відрізок  проходить через точку . Згідно з теоремою синусів

, .

Оскільки  і , то .

Аналогічні співвідношення можна записати і для відрізків, які з'єднують середини двох інших пар протилежних сторін. Перемножуючи ці співвідношення, одержуємо необхідне.

Задача 3.11. Через точки  і , що лежать на колі, проведено дотичні, які перетина-ються в точці . На дузі  взяті точки  і . Прямі  і  перетинаються в точці ,  і  – у точці . Довести, що пряма  проходить через точку .

Доведення.

Згідно з теоремою Чеви у формі синусів

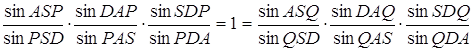
Але.

Тому .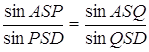

З цього випливає, що точки  лежать на одній прямій, оскільки функція  монотонна по :

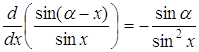
Задача 3.12. а) На сторонах  рівнобедреного трикутника  з основою  взяті точки  так, що прямі  перетинаються в одній точці. Довести, що

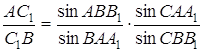
б) В середині рівнобедреного трикутника  з основою  взяті точки  і  так, що  і . Довести, що точки  лежать на одній прямій.

Доведення.

а) Згідно з теоремою Чеви

,

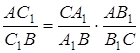а по теоремі синусів

Підставляючи ці чотири рівності в попередню рівність, і враховуючи, що , одержуємо необхідне.

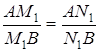б) Позначимо точки перетину прямих  і  з основою  через  і . Потрібно довести, що . З а) випливає, що , тобто .

Задача 3.13. У трикутнику  проведені бісектриси . Бісектриси  перетинають відрізки  та  в точках . Довести, що .

Доведення.

Нехай відрізки  і  перетинають сторону  в точках  і . Тоді

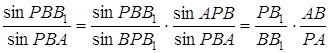
Якщо  – точка перетину бісектрис трикутника , то

,

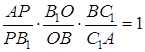отже,

.

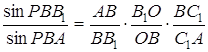Помітивши, що 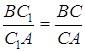, і проводячи аналогічні обчислення для 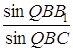, одержимо .

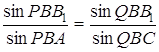Оскільки , то .

Задача 3.14. На сторонах  трикутника  взяті точки , при цьому  перетинаються в одній точці. Довести, що .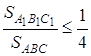

Доведення

Нехай . Тоді

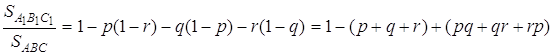
Згідно з теоремою Чеви

,

тобто .

Крім того,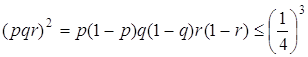

Отже, .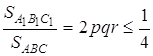

Задача 3.15. На сторонах трикутника  у зовнішню сторону побудовані квадрати.  – середини протилежних сторін квадратів, побудованих на  відповідно. Довести, що прямі  перетинаються в одній точці.

Доведення.

Нехай  – точки перетину прямих  зі сторонами  відповідно.

Відношення  дорівнює відношенню висот, які опущено з точок  та  на сторону , тобто дорівнює відношенню .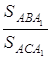

Далі,

,

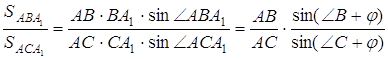де .

Аналогічно,

, .

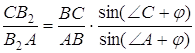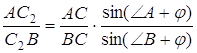Перемножуючи ці рівності, маємо

.

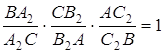Згідно з теоремою Чеви прямі  перетинаються в одній точці.

Задача 3.16. Нехай з точки , яка взята зовні кола, проведені дві дотичні  і  до кола та дві січні, і нехай  та  – точки перетину кола з першою січною, а точки  та  – з другою. Тоді прямі  і  перетинаються в одній точці.

Доведення.

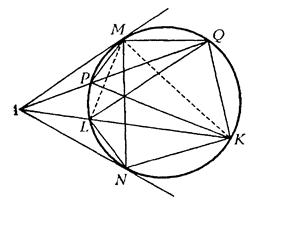
Застосуємо теорему Чеви до трикутника . Прямі  і  перетинаються в одній точці, якщо виконується рівність

(*)

Всі кути, що фігурують в останньому співвідношенні, – вписані в задане коло; синуси цих кутів пропорційні довжинам хорд, що стягаються ними (наприклад, , де  – радіус кола).Тому рівність (*) еквівалентна такій рівності:

(**)

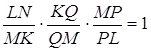Покажемо, що (**) насправді виконується. З подоби трикутників  й  одержуємо 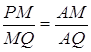. З подоби трикутників  і  маємо , і нарешті, з подоби трикутників  і  знаходимо .

Перемножуючи останні три рівності, маємо (*)

.

 

Задача 3.17. Трикутник  вписано в трикутник : вершини  лежать на сторонах  відповідно. Довести, що якщо прямі, які проведені через вершини трикутника  перпендикулярно до відповідних сторін трикутника , перетинаються в одній точці, то прямі, які проведені через вершини трикутника  перпендикулярно до відповідних сторін трикутника  перетинаються в одній точці.

Доведення.

Нехай прямі, які проходять через вершини трикутника  перпендикулярно до відповідних сторін трикутника , перетинаються в точці .

Оскільки точки  лежать на колі, побудованому на відрізку  як на діаметрі, то . Опустимо з точки  перпендикуляр  на пряму . Оскільки , то , тобто пряма  симетрична прямій  відносно бісектриси кута .

Аналогічні міркування для інших кутів показують, що перпендикуляри , які опущені з вершин трикутника  на сторони трикутника  симетричні прямим  відносно бісектрис трикутника . Згідно з задачею 3.9 прямі  перетинають в одній точці.

Задача 3.18 (теорема Ван Обеля). На сторонах  трикутника  взято точки , так що прямі  перетинаються в одній точці. Довести, що

.

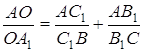Доведення.

Нехай прямі  перетинають пряму, яка проходить через точку  паралельно прямій , в точках  і .

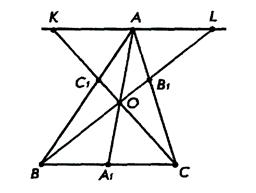
Оскільки трикутник  подібний до трикутника , трикутник  подібний до трикутника  за першою ознакою подібності трикутників, то 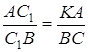; 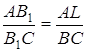. Додавши ці рівності і, враховуючи, що , одержуємо:

.

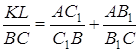Далі, трикутник  подібний до трикутника  і трикутник  подібний до трикутника .

Тому ; .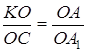

Звідси випливає, що 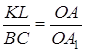. З цієї рівності і рівності  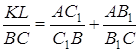безпосередньо випливає, що

.

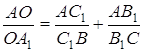Задача 3.19 Задано трикутник . Довести, що чевіани , які ділять його периметр навпіл, перетинаються в одній точці.

Доведення.

Нехай довжини сторін  відповідно , тоді число  згідно з нерівністю трикутника додатнє і менше .

Нехай точка  лежить на стороні  і така, що . Зрозуміло, що пряма  ділить периметр трикутника  навпіл, аналогічно з точками  і  (можна помітити, що  – точки дотику вневписаних кіл трикутника ).

Переконавшись в існуванні потрібних точок, розв’яжемо основну задачу.

Для цього обчислюємо довжини всіх необхідних відрізків.

, , ,

, , .

Зрозуміло, що 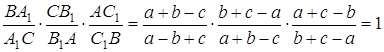, отже чевіани  перетинаються в одній точці.

РОЗДІЛ 4

ТЕОРЕМИ ЧЕВИ ТА МЕНЕЛАЯ НА ПЛОЩИНІ

 

Означення. Під кутом  між двома векторами  і  будемо розуміти кут, на який необхідно повернути вектор у додатньому напрямку (проти ходу годинної стрілки) до збігу з напрямком вектора (див. рис. 4.1).

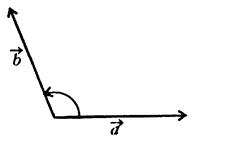
Рис. 4.1 До визначення кута між двома векторами

Нехай для визначеності, що . З означення і властивостей функції  випливає, що

.

Розглянемо два трикутники: (позначимо його через ) і , вершини  і  якого лежать на прямих  і  відповідно; позначимо трикутник  через . Зрозуміло, що вектори і коллінеарні; також коллінеарні й вектори . Введемо для коллінеарних векторів  і  величину 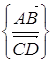, яка дорівнює відношенню довжин векторів  і , взятому зі знаком “+” , якщо вектори і співнаправлені, і зі знаком “–“ у супротивному випадку.

 

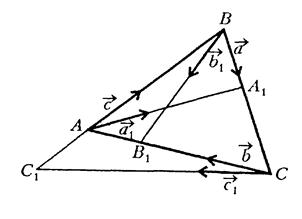
Рис. 4.2

Визначимо для трикутників  і  величину :

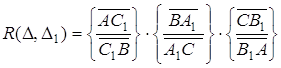(4.1)

Нехай далі  – трійка векторів , які коллінеарні векторам  (сторонам трикутника )  – трійка векторів , які коллінеарні векторам і . Визначимо для  і  величину

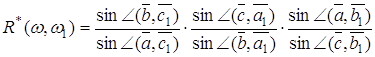(4.2)

 

Лема. (4.3)

Доведення. Спочатку перевіримо, що  та  одного знака. Легко переконатися, що зміна напрямку одного з векторів , не змінить величини , тому можна обрати напрямок кожного з них певним чином; наприклад, можна вважати вектори , такими, що збігаються за напрямком з векторами , ,і  (див. рис. 4.2) .

У цьому випадку кожний з трьох дробів, що входять у вираз  має той самий знак, що і відповідний дріб, який входить у вираз .

Наприклад, дроби

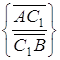 і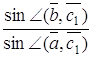

будуть додатними, якщо точка  розташована між точками  і , і від’ємними супротивному випадку (див. рис. 4.2, 4.3).

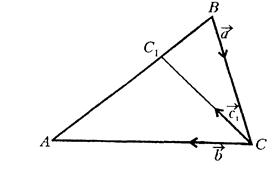
Рис. 4.3

Залишилось довести, що . Маємо

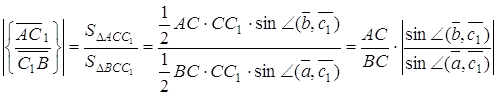
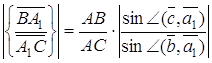
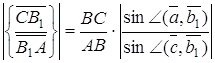
Перемножуючи ці три рівності, одержимо, що . Лема доведена.

Далі буде необхідна рівність, що безпосередньо випливає з означення :

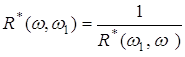. (4.4)

Сформулюємо тепер теореми Чеви та Менелая.

Теорема Чеви. Для того, щоб прямі  і  перетиналися в одній точці, необхідно і достатньо, щоб виконувалась рівність

(4.5)

або еквівалентна рівність

(4.5^/)

 

Теорема Менелая. Для того, щоб точки  лежали на одній прямій, необхідно і достатньо, щоб виконувалась рівність

 (4.6)

або еквівалентна рівність

(4.6^/)

Доведення теореми Чеви.

Необхідність. Нехай прямі ,  перетинаються в одній точці. Доведемо, що виконуються умови (4.5) і (4.5^/).

Якщо прямі і  перетинаються в одній точці, то або всі три точки  і  лежать на сторонах трикутника , або одна з точок лежить на стороні трикутника, а дві інші – на продовженнях відповідних сторін.

У першому випадку всі дроби, що входять у вираз , додатні, а в другому випадку один із трьох дробів, що входить у вираз , додатний, а два інші – від’ємні, так що знову вираз (а отже, і  – див. лему) більше нуля.

Доведемо, що  (оскільки >0, то з цього буде випливати, що  дорівнює одиниці).

Позначимо точку перетину прямих  і  через (рис. 4.4а).

а)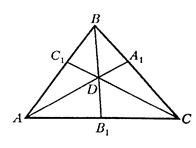

б)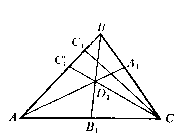

Рис. 4.4

Застосовуючи теорему синусів, одержимо

,

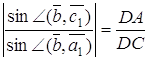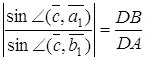
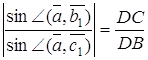
Перемножуючи ці рівності, знаходимо , тим самим необхідність доведена.

Достатність. Доведення достатності проведемо методом від супротивного.

Припустимо, що , але прямі  , і  не проходять через одну крапку (див. рис. 4.4б).

Позначимо точку перетину прямих і  через  , а через  – точку перетину прямих  і . Оскільки прямі  , і  перетинаються в одній точці, то

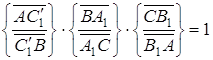
Але за умовою

,

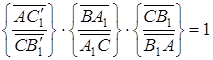звідки 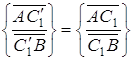. Так як і точка  і точка лежать на прямій , то з цього випливає, що точки  та  збігаються.

Теорема Чеви доведена.

Доведення теореми Менелая

Необхідність. Відомо, що точки  і  лежать на одній прямій. Необхідно довести рівності (4.6) та (4.).

Якщо точки  і  лежать на одній прямій, то або усі вони знаходяться на продовженнях  і  сторін трикутника , або ж дві з точок  знаходяться на відповідних ним сторонах, а третя – на продовженні.

В обох випадках вираження  буде від’ємним. Доведемо тепер, що якщо точки  – на одній прямій, то  (оскільки <0, з цього буде випливати, що ).

Проведемо через точку  пряму, паралельну , і позначимо точку її перетину з прямою  через  (див. рис. 4.5).

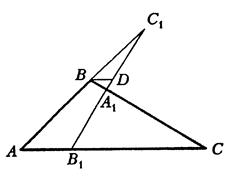
Рис. 4.5

Використовуючи подібність, одержимо

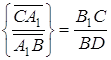
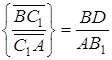
Додавши рівність 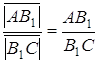 і перемноживши всі три рівності, одержимо, що . Необхідність умов теореми Менелая доведена.

Достатність. Доведення достатності умов (4.6) і (4.) теореми Менелая проводиться аналогічно доведенню достатності умов (4.5) і (4.) теореми Чеви.

Теорема доведена.

ВИСНОВКИ

Розв’язок задач складає суттєву сторону процесу навчання математиці: рівень математичної підготовки в більшості визначається глибиною навиків у розв’язанні задач.

Ці обставини спонукають з особливою увагою відноситись до організації в середніх школах, гімназіях та ліцеях ретельно продуманих занять, які мають за мету надати учням не тільки теоретичні знання в області геометрії, але й навчити їх вільно застосовувати здобуті знання до розв’язання нестандартних задач середньої та підвищенної складності.

Останнім часом у варіантах вступних іспитів все частіше зустрічаються задачі, розв’язок яких суттєво спрощується за допомогою теорем Чеви та Менелая.

Дипломна робота присвячена вивченню теорем Чеви та Менелая на площині та в просторі, доведенню нетривіальних наслідків цих теорем та розв’язанню задач за допомогою цих теорем.

Теорема Менелая має широке застосування при доведенні теорем (наприклад, теорем Дезарга, Паппа, Паскаля, Гаусса та інших) та розв’язанні задач. Теорема Менелая дозволяє знаходити відношення відрізків, а також доводити належність трьох точок одній прямій. В роботі наведено багато задач, розв’язаних двома способами: традиційним і за допомогою теореми Менелая, при цьому останній спосіб розв’язання задач виявляється більш раціональним (розв’язок задачі займає всього кілька рядків). Зазначимо, що при розв’язку задач найскладнішою справою є пошук трикутника, до якого слід застосувати теорему Менелая.

Теореми Чеви використовується при розв’язуванні задач про трійки прямих, що проходять через одну точку, а також при доведенні теорем про перетин трійок прямих в одній точці.

В роботі також розглянуто аналоги теорем Чеви та Менелая в просторі.

Наведені в дипломній роботі задачі (розв’язано 50 задач) можуть бути використані при позакласній роботі з учнями (на заняттях гуртків, при проведенні математичних олімпіад, для індивідуальної роботи з найбільш здатними учнями).

СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ

 

1. Атанасян Л.С., Денисова Н.С., Силаев Е.В. Курс элементарной геометрии. 1 часть. Планиметрия. – М.: Сантакс-Пресс, 1997. – 304 с.

2. Буник І. Теорема Менелая // Математика. – №15(315), квітень, 2005. – с.17-21.

3. Габович И. Теорема Менелая для тетраэдра // КВАНТ, №6, 1996, с. 34-36.

4. Готман Э.Г., Скопец З.А. Задача одна – решения разные.–К.: Рад. шк.–1988.–173с.

5. Егоров А. Теоремы Чевы и Менелая // КВАНТ, №3, 2004, с.35-38.

6. Зетель С.И. Новая геометрия треугольника. – М., – 1962. – С. 151.

7. Карп А.П. Даю уроки математики…: Кн. для учителя: Из опыта работы. – М.: Просвещение, 1992. – 191 с.

8. Коксетер Г.С., Грейтцер С.Л. Новые встречи с геометрией. – М.: Наука, 1978. – 223 с.

9. Куланин Е. Об одной трудной геометрической задаче // КВАНТ, №7,1992.–с.46-50

10. Орач Б. Теорема Менелая // КВАНТ, №3, 1991, с. 52-55.

11. Прасолов В.В. Задачи по планиметрии, ч.1. – М.: Наука, 1986. – 272 с.

12. Прасолов В.В. Задачи по планиметрии, ч.2. – М.: Наука, 1991. – 240 с.

13. Прасолов В.В., Шарыгин И.Ф. Задачи по стереометрии.–М.: Наука, 1989. – 288 с.

14. Скопец З.А., Жаров В.А. Задачи и теоремы по геометрии (планиметрия). – М., 1962. – 162 с.

15. Скопец З.А., Понарин Я.П. Геометрия тетраэдра и его элементов. – Ярославль, 1974. – 239 с.

16. Страшевич С., Бровкин Е. Польские математические олимпиады. Пер. с польск. Ю.А. Данилова под ред. В.М. Алексеева. – М.: Мир, 1978. – 338 с.

17. Шарыгин И. Ф. Теоремы Чевы и Менелая // КВАНТ, №11, 1976.

18. Шарыгин И.Ф. Задачи по геометрии: Планиметрия. – М.: Наука, 1986.

19. Шклярский Д.О., Ченцов Н.Н., Яглом И.М. Избранные задачи и теоремы планиметрии. – М.: Наука, 1967.

20. Эрдниев Б., Манцаев Н. Теоремы Чевы и Менелая // КВАНТ, №3, 1990, с. 56-59.