Поиски более рационального способа решения систем линейных уравнений с двумя переменными - методом подстановки

Министерство образования и науки Республики Казахстан

Алматинская область Карасайский район

Секция: математическая

ТЕМА: Поиски более рационального способа решения систем линейных уравнений с двумя переменными - методом подстановки

Школа им. Ш. Кудайбердыулы

Ученик 8 класса

Басов Ярослав Андреевич

Научный Руководитель:

Нигматуллина Ирина Ильдаровна

Научный консультант:

Поселок Нурлытау 2009 г.

План

Введение

Глава 1. Цель исследования

Глава 2. Методика исследования данной работы

Глава 3. Результаты исследования и их практическая значимость

Список использованной литературы

Приложение

Введение

Основная цель при решении систем линейных уравнений - решить систему уравнений, то есть найти все ее решения или доказать, что решений нет. Для решения системы уравнений с двумя переменными используются:

1-графический способ,

2. способ подстановки,

3 - способ сложения.

Практическое применение этих способов - это решение задач, по алгебре, физике, химии, геометрии.

1 - Кроме этого умение определить без построения графиков число решений системы линейных уравнений с числовыми коэффициентами. Основная цель, которая ставится при изучении темы - понять, то, что вопрос о числе решений системы двух линейных уравнений (если исключить выраженный случай а=0, в=0 для линейного уравнения ах + ву = с) сводиться к определению числа общих точек прямых, являющимися графиками уравнений системы.

Известно, что графиком линейного уравнения является прямая.

Рассмотрим три случая расположения прямой.

Случай 1.

Прямые, являющиеся графиком уравнения, входящих в эту систему, пересекаются. Решим систему уравнений:

 

Уравнениями у = - 1, Iх + 12 и у = - 6х + 18 задаются линейные функции. Угловые коэффициенты прямых, являющихся графиками этих функций, различны. Значит, эти прямые пересекаются, и система имеет единственное решение. Прировняв правые части уравнений, найдем точку пересечения Данная система имеет единственное решение: пара чисел.

Случай 2.

Прямые, являющиеся графиками уравнений системы, параллельны. Решим систему уравнений:

 

Прямые, являющиеся графиками линейных функций у = - О,4х+О,15 и

У = - О,4х+3,2, параллельны, так как их угловые коэффициенты одинаковы, а точки пересечения с осью у различны. Отсюда следует, что данная система уравнений не имеет решений

Случай 3.

Прямые, являющиеся графиками уравнений системы, совпадают.

 

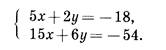
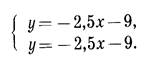
Очевидно, что графики уравнений совпадают. Это означает, что любая пара чисел (х; у), в которой х - произвольное число, а у = - 2,5х - 9, является решением системы. Система имеет бесконечно много решений.

Главная проблема при решении системы линейных уравнений графическим способом у учащихся это?

не умения, выражать одну переменную через другую.

не правильное построение системы координат (различный единичный отрезок на осях ординат и абсцисс).

Рассмотрим способ решения систем линейных уравнений с двумя переменными, называемый способом подстановки. Начнем с задачи.

Ученик задумал два числа. Первое число на 7 больше второго. Если от утроенного первого числа вычесть удвоенное второе число, то получится 27 Какие числа задумал ученик?

Решение: Пусть х - первое число, у - второе число. По условию задачи составим систему уравнений.

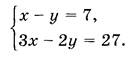
В первом уравнении выразим х через у: х = у + 7.

Подставив во второе уравнение вместо переменной х выражение х = у + 7, получим систему

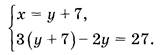
Второе уравнение системы представляет собой уравнение с одной переменной.

Решим его:

Зу+2I-2у=27; у=6.

Подставив в первое уравнение системы вместо переменной у ее значение, равное 6, получим:

х=6+ 7;

х= 13.

Пара чисел (13;

6) является решением системы. Ответ: (13;

6).

Главная проблема при решении системы линейных уравнений способом подстановки у учащихся это?

не умения, выражать одну переменную через другую.

не умение, подставить уже полученную переменную (не видят)

Рассмотрим еще один способ решения систем линейных уравнений - способ сложения. При решении систем этим способом, как и при решении способом подстановки, мы переходим от данной системы к другой, равносильной ей системе, в которой одно из уравнений содержит только одну переменную.

Решим систему уравнений:

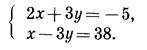
В уравнениях этой системы коэффициенты при у являются противоположными числами. Сложив почтенно левые и правые части уравнений, получим уравнение с одной переменной:

3х = 33.

Заменим одно из уравнений системы (1), например первое, уравнением 3х=33. Получим систему:

Система (2) равносильна системе (1). Решим систему (2). Из уравнения 3х=33 находим, что х=11. Подставив это значение х в уравнение х-3у=38, получим уравнение с переменной у:

Решим это уравнение:

II-Зу=38.

3у=27,у= - -9.

Пара (11; - 9) - решение системы (2), а значит, и данной системы (1).

Воспользовавшись тем, что в уравнениях системы (1) коэффициенты при у являются противоположными числами, мы свели ее решение к решению равносильной системы (2), в которой одно из уравнений содержит только одну переменную.

Геометрически равносильность систем (1) и (2) означает, что графики уравнений 2х+3у= - 5 и х-3у=38 пересекаются.

Главная проблема при решении системы линейных уравнений способом подстановки у учащихся это?

1) не умение, подставить уже полученную переменную (не видят)

Проанализировав основные проблемы решение линейных систем уравнений с двумя переменными, можно сделать вывод:

Главная проблема при решении систем линейных уравнений различными способами у учащихся это?

не умения, выражать одну переменную через другую. (в трех случаях)

не умение, подставить уже полученную переменную (в двух случаях)

И обе эти проблемы встречаются при решении линейных систем уравнений способом подстановки.

Почему я решил проводить исследование в этой области?

Проанализировав основные проблемы решение линейных систем уравнений с двумя переменными, можно сделать вывод.

Главная проблема при решении систем линейных уравнений различными способами у учащихся это?

не умения, выражать одну переменную через другую. (в трех случаях)

не умение, подставить уже полученную переменную (в двух случаях)

И обе эти проблемы встречаются при решении линейных систем уравнений способом подстановки.

Кроме этого, решение задач составлением систем уравнений, по физике, алгебре, геометрии и химии для таких учащихся останутся недоступными. Поэтому я решил, заняться, поиском более рационального способа решения систем линейных уравнений с двумя переменными - методом подстановки.

Я считаю, что моя работа, в этом направлении очень актуальна.

Глава 1. Цель исследования