Навигация
Рассмотрим систему 3-х линейных уравнений с тремя неизвестными
1. Рассмотрим систему 3-х линейных уравнений с тремя неизвестными.
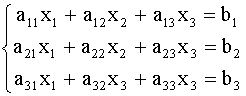 (2).
(2).
Метод Гаусса решения системы (2) состоит в следующем: Разделим все члены первого уравнения на ![]() , а затем, умножив полученное уравнение на
, а затем, умножив полученное уравнение на ![]() , вычтем его соответственно из второго и третьего уравнений системы (2). Тогда из второго и третьего уравнений неизвестное
, вычтем его соответственно из второго и третьего уравнений системы (2). Тогда из второго и третьего уравнений неизвестное ![]() будет исключено, и получиться система вида:
будет исключено, и получиться система вида:
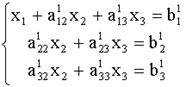 (3)
(3)
Теперь разделим второе уравнение системы (3) на ![]() , умножим полученное уравнение на
, умножим полученное уравнение на ![]() и вычтем из третьего уравнения. Тогда из третьего уравнения неизвестное
и вычтем из третьего уравнения. Тогда из третьего уравнения неизвестное ![]() будет исключено и получиться система треугольного вида:
будет исключено и получиться система треугольного вида:
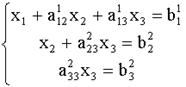 (4)
(4)
Из последнего уравнения системы (4) находим ![]() , подставляя найденное
, подставляя найденное
подставляя найденное значение в первое уравнение, находим ![]() .
.
Методом Гаусса решить систему:
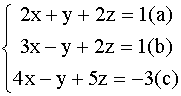
Решение: Разделив уравнение (а) на 2, получим систему
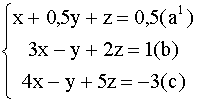
Вычтем из уравнения (b) уравнение ![]() , умноженное на 3, а из уравнения (c) - уравнение
, умноженное на 3, а из уравнения (c) - уравнение ![]() , умноженное на 4.
, умноженное на 4.
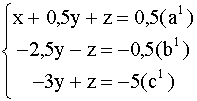
Разделив уравнение ![]() (
(![]() ) на - 2,5, получим:
) на - 2,5, получим:
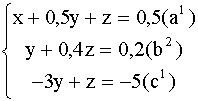
Вычтем из уравнения (![]() ) уравнение
) уравнение ![]() , умноженное на - 3:
, умноженное на - 3:
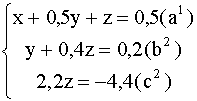
Из уравнения ![]() находим Z=-2; подставив это значение в уравнение
находим Z=-2; подставив это значение в уравнение ![]() , получим Y=0,2-0,4Z=0,2-0,4 (-2) =1; наконец, подставив значение Z=-2 и Y=1 в уравнение (a 1), находим X=0,5-0,5Y-Z=0,5-0,5 1 - (-2) =2. Итак, получаем ответ X=2, Y=1, Z=-2.
, получим Y=0,2-0,4Z=0,2-0,4 (-2) =1; наконец, подставив значение Z=-2 и Y=1 в уравнение (a 1), находим X=0,5-0,5Y-Z=0,5-0,5 1 - (-2) =2. Итак, получаем ответ X=2, Y=1, Z=-2.
Проверка:
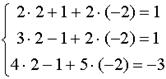
Линейные уравнения.
Уравнения вида ax+b=0, где a и b - некоторые постоянные, называется линейным уравнением.
Если a¹0, то линейное уравнение имеет единственный корень: x = - b /a.
Если a=0; b¹0, то линейное уравнение решений не имеет.
Если a=0; b=0, то, переписав исходное уравнение в виде ax = - b, легко видеть, что любое x является решением линейного уравнения.
Уравнение прямой имеет вид: y = ax + b.
Если прямая проходит через точку с координатами X0 и Y0, то эти координаты удовлетворяют уравнению прямой, т.е. Y0 = aX0 + b.
Пример 1.1 Решить уравнение
2x - 3 + 4 (x - 1) = 5.
Решение. Последовательно раскроем скобки, приведём подобные члены и найдём x: 2x - 3 + 4x - 4 = 5, 2x + 4x = 5 + 4 + 3,6x = 12, x = 2.
Ответ: 2.
Пример 1.2 Решить уравнение 2x - 3 + 2 (x - 1) = 4 (x - 1) - 7.
Решение.2x + 2x - 4x = 3 +2 - 4 - 7, 0x = - 6.
Ответ: Æ.
Пример 1.3 Решить уравнение.
2x + 3 - 6 (x - 1) = 4 (x - 1) + 5.
Решение.
2x - 6x + 3 + 6 = 4 - 4x + 5,- 4x + 9 = 9 - 4x,
4x + 4x = 9 - 9,0x = 0.
Ответ: Любое число.
Системы линейных уравнений.
Уравнение вида
a1x1 + a2x2 + … + anxn = b,
где a1, b1, …,an, b - некоторые постоянные, называется линейным уравнением с n неизвестными x1, x2, …, xn.
Система уравнений называется линейной, если все уравнения, входящие в систему, являются линейными. Если система из n неизвестных, то возможны следующие три случая:
система не имеет решений;
система имеет ровно одно решение;
система имеет бесконечно много решений.
Пример: решить систему уравнений
![]() x + y - z = 2,2
x + y - z = 2,2
x - y + 4z = 1,
x + 6y + z = 5.
Решение. При решении систем линейных уравнений удобно пользоваться методом Гаусса, который состоит в преобразовании системы к треугольному виду.
Умножаем первое уравнение системы на - 2 и, складывая полученный результат со вторым уравнением, получаем - 3y + 6z = - 3. Это уравнение можно переписать в виде y - 2z = 1. Складывая первое уравнение с третьим, получаем 7y = 7, или y = 1.
Таким образом, система приобрела треугольный вид
![]() x + y - z = 2,
x + y - z = 2,
y - 2z = 1 ,y = 1.
Подставляя y = 1 во второе уравнение, находим z = 0. Подставляя y =1 и z = 0 в первое уравнение, находим x = 1.
Ответ: (1; 1; 0).
Системы уравнений второй степени.
В простейших случаях при решении систем уравнений второй степени удаётся выразить одно неизвестное через другое и подставить это выражение во второе уравнение.
При решении систем уравнений второй степени часто используется также способ замены переменных.
Пример. Среди решений (x; y) системы найти то, для которого сумма (x + y) максимальна. Вычислить значение этой суммы.
![]() 2x + y = 7,
2x + y = 7,
xy = 6.
Решение. Из первого уравнения получаем y = 7 - 2x. Подставляя значение y во второе уравнение, получаем систему уравнений
![]() y = 7 - 2x,
y = 7 - 2x,
7x - 2x2 = 6.
Квадратное уравнение - 2x2 + 7x - 6 = 0 имеет корни X1 = 2; X2 = 3/2. Из первого уравнения получаем Y1 = 3; Y2 = 4.
Решения имеют вид (2;3) и (1,5;4). Наибольшая сумма x + y = 1,5 + 4 = 5,5.
Ответ: 5,5.
Метод введения новых неизвестных при решении уравнений и систем уравнений.
При решении биквадратных и возвратных уравнений мы вводили новые неизвестные (у = х2 для биквадратных уравнений и у = х + 1/х для возвратных уравнений). Введение новых неизвестных применяется также при решении уравнений иного вида и систем уравнений.
Пример Решим уравнение 12/ (х2 + 2х) - 3/ (х2 + 2х - 2) = 1.
Решение. Если попробовать привести дробь в левой части уравнения к одному знаменателю, то получим уравнение четвёртой степени, которое мы умеем решать.
Чтобы решить заданное уравнение, заметим, что в обе дроби входит одно и то же выражение х2 + 2х. Поэтому введём новое неизвестное у, положив, что у = х2 + 2х. Тогда уравнение примет вид
12/у - 3/ (у - 2) = 1 или (у2 - 11у + 24) / (у (у - 2)) = 0,откуда y1 = 3; y2 = 8. Осталось решить уравнения х2 + 2х = 3 (его корни х1 = 1, х2 = -3) и х2 + 2х = 8 (его корни х3 = 2, х4 = -4).
Применённый метод называется методом введения новых неизвестных, и его полезно применять, когда неизвестное входит в уравнение всюду в виде одной и той же комбинации (особенно если эта комбинация содержит степени неизвестного выше первой).
Пример. Решим систему уравнений
![]()
2/х + 3/у = 8,5
/х - 2/у = 1.
Решение.
Обозначим 1/х через U, а 1/у через V.
Тогда система примет вид
![]() 2U + 3V = 8,5
2U + 3V = 8,5
U - 2V = 1,
т.е. получится система двух линейных уравнений с двумя неизвестными U и V. Из первого уравнения выражаем U через V: U = 4 - 3V / 2, и подставляя во второе: 5 (4 - 3V / 2) -2V = 1, откуда V = 2. Теперь находим U = 1 и решаем уравнения 1/x = 1, 1/y = 2.
Ответ: x = 1, y = 0,5.
Однородные уравнения.
Пример Решим систему уравнений
![]() 8х2 - 6ху + у2 = 0,
8х2 - 6ху + у2 = 0,
х2 + у2 = 5.
Решение. заметим, что для решения системы выполняется условие у ¹ 0. В самом деле, из первого уравнения следует, что если у = 0, то и х = 0, а числа х = 0 и у = 0 не удовлетворяют второму уравнению системы. Разделим первое уравнение на у2.
Получится уравнение
8х2/у2 - 6ху / у2 + у2/у2 = 0 или
8х2/у2 - 6х / у + 1 = 0.
Введём вспомогательное неизвестное U = х / у.
Уравнение примет вид
8U2 - 6U + 1 = 0.
Это квадратное уравнение, имеющее корни U1 = 0,5; U2 = 0,25. Таким образом, из первого уравнения мы получаем что либо x / y = 1/2, либо x / y = 1/4. Осталось подставить выражения у =2х и у = 4х (рассмотрев оба случая) во второе уравнение системы. В первом случае получается уравнение 5х2 = 5, откуда х1 = 1, х2 = - 1; соответственно у1 = 2, у2 = - 2.
Во втором случае получается уравнение17х2 = 5, откуда х3 = Ö (5/17), x4 = -Ö (5/17); соответственно y3 = 4Ö (5/17), y4 = - 4Ö (5 /17).
Первое уравнение системы нам удалось представить как уравнение относительно x / y благодаря тому, что степень всех членов, входящих слагаемыми в это уравнение (8x2, 6xy, y2), одна и та же - она равна двум. Поэтому после деления на y2 каждое слагаемое выразилось через x / y.
Многочлен от двух переменных x и y такой, что степень каждого его члена равна одному и тому же числу k, называется однородным многочленом степени k.
Уравнение вида P (x, y) = 0 называется однородным уравнением степени k относительно x и y, если P (x, y) - однородный многочлен степени k. Однородное уравнение относительно x и y делением на yk (если y = 0 не является корнем уравнения) превращается в уравнение относительно неизвестного x / y. Это свойство однородного уравнения помогает решать многие задачи.
Решение симметрических систем уравнений.
Напомним, что многочлен P (x, y) называется симметрическим, если P (x, y) = P (y, x).
При решении систем уравнений вида
![]() P1 (x, y) = 0,
P1 (x, y) = 0,
P2 (x, y) = 0,
где P1 (x, y) и P2 (x, y) - симметрические многочлены, полезной оказывается такая замена неизвестных: x + y = U, xy = V. Напомним, что любой симметрический многочлен P (x, y) можно представить как выражение от U и V.
Пример Решить систему уравнений
![]() x2 + xy + y2 = 49,
x2 + xy + y2 = 49,
x + y + xy = 23.
Решение. Заметим, что:
x2 + xy + y2 = x2 + 2xy + y2 - x
y = (x + y) 2 - xy.
Сделаем замену неизвестных: x + y = U, xy =V.
Система примет вид:
![]() U2 - V = 49,
U2 - V = 49,
U + V = 23.
Сложив эти уравнения, получим уравнение U2 + U - 72 = 0 с корнями U1 = 8,U2 = -9. Соответственно V1 = 15, V2 = 32. Остаётся решить системы уравнений:
![]() x + y = 8,xy = 15,
x + y = 8,xy = 15,
![]() x + y = - 9,xy = 32.
x + y = - 9,xy = 32.
![]() Система x + y = 8, имеет решения:
Система x + y = 8, имеет решения:
x1 = 3, y1 = 5; x2 = 5,
y2 = 3.xy = 15.
Система x + y = - 9, действительных решений не имеет. Ответ: x1 = 3, y1 = 5; x2 = 5, y2 = 3.
Глава 2. Методика исследования данной работыМетодика исследовании.
Моя основная цель, найти более рациональный способ решения систем линейных уравнений с двумя переменными - методом подстановки.
Поэтому я решил использовать метод “Искусство", т.е. решать примеры нестандартно, придумать “свой метод", догадаться что-то прибавить и отнять, выделить полный квадрат, на что-то разделить и умножить и т.д.
При решении систем уравнений второй степени часто используется также способ замены переменных - его я тоже решил применить.
Итак, для решения проблемы я решил использовать два методы решений:
Похожие работы
... ;[0; 1), тогда x – x +1 = 1; 1 = 1 Þ x — любое число из [0; 1). В) x Î[1; ¥), тогда x + x – 1 = 1; 2x = 2; x = 1 Î[1; ¥). Ответ: x Î[0; 1]. Основные методы решения рациональных уравнений. 1) Простейшие: решаются путём обычных упрощений — приведение к общему знаменателю, приведение подобных членов и так далее. Квадратные уравнения ax2 + bx + c = 0 решаются по ...
... на качественно новую ступень овладения содержанием школьной математики. Глава II. Методико - педагогические основы использования самостоятельной работы, как средство обучения решению уравнений в 5 - 9 классах. § 1. Организация самостоятельной работы при обучения решению уравнений в 5 - 9 классах. При традиционном способе преподавания учитель часто ставит ученика в положение объекта ...
... точек координатной оси. Занятие № 4. Тема: Аналитический метод. Метод «ветвлений». Цель занятия: познакомить учеников с основным методом решения уравнений, содержащих параметр. Литература для учителя: см. [1] , [5], [6], [7], [14] Литература для ученика: см. [3] Краткое содержание: рассмотрение различных значений, принимаемых параметром. Упрощение уравнения и приведение уравнения к произведению ...
... Келли), исследования экспериментального изучения относительно частных процессов и функций мыслительной деятельности (Ж. Пиаже), создания концепций когнитивной структуры личности, связанной с развитием интеллекта в процессе обучения (Дж. Брунер, Д. Озбел) появляется критическая информация в связи с отсутствием концептуального единства многочисленных теорий. В последнее время мы можем обнаружить ...
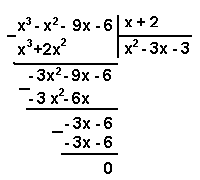


0 комментариев