Навигация
Найдите произведение корней уравнения
5. Найдите произведение корней уравнения
![]() Ответ:
Ответ: ![]() .
.
6. ![]() Ответ:
Ответ: ![]() .
.
7.  Ответ:
Ответ: ![]() .
.
8. ![]() Ответ:
Ответ: ![]() .
.
9. ![]() Ответ:
Ответ: ![]()
10. ![]() Ответ:
Ответ: ![]() .
.
11. ![]() Ответ: 2; 3; 4; 11.
Ответ: 2; 3; 4; 11.
12. ![]() Ответ:
Ответ: ![]() .
.
13. 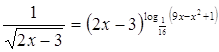 Ответ:
Ответ: ![]() .
.
14. ![]() Ответ:
-2; 0; 2.
Ответ:
-2; 0; 2.
15. 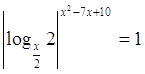 Ответ:
1; 4; 5.
Ответ:
1; 4; 5.
16. ![]() Ответ:
нет решений.
Ответ:
нет решений.
17. 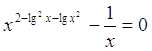 Ответ:
1; 10; 10-3.
Ответ:
1; 10; 10-3.
18. ![]() Ответ: 1; 8.
Ответ: 1; 8.
19. ![]() Ответ: -1; 1; 2.
Ответ: -1; 1; 2.
20. ![]() Ответ:
Ответ:
![]() .
.
21. ![]() Ответ:
2; 10-1; 10-3.
Ответ:
2; 10-1; 10-3.
22. ![]() Ответ:
0; 3.
Ответ:
0; 3.
23. 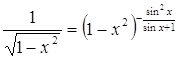 Ответ:
0.
Ответ:
0.
24. ![]() Ответ:
Ответ:
![]() .
.
25. ![]() Ответ:
Ответ:
![]() .
.
26. ![]()
Ответ:
![]() .
.
27. ![]() Ответ:
Ответ:
![]() .
.
28. ![]()
Ответ:
![]() .
.
29. ![]() Ответ:
Ответ: ![]() .
.
30. ![]() Ответ:
Ответ:
![]() .
.
31. 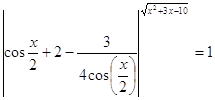
Ответ: ![]() .
.
32. 
Ответ: ![]() .
.
33. 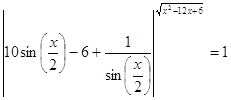
Ответ:
![]() .
.
34.![]() Ответ: 0; 1.
Ответ: 0; 1.
35. ![]() Ответ:
1; 3.
Ответ:
1; 3.
36. ![]() Ответ:
0; 1; 5.
Ответ:
0; 1; 5.
37. ![]() Ответ:
0; 5; 4.
Ответ:
0; 5; 4.
38. ![]()
Ответ:
![]() .
.
39. ![]() Ответ:
Ответ: ![]() .
.
40. ![]() Ответ:
Ответ: ![]() .
.
41. ![]() Ответ:
Ответ:
![]() .
.
42. ![]() Ответ:
Ответ: ![]() .
.
43. ![]() Ответ:
1; 0,1; 0,01.
Ответ:
1; 0,1; 0,01.
44. ![]()
45. ![]() Ответ: -2; -1; 3.
Ответ: -2; -1; 3.
46. ![]() Ответ: -2; 0,6.
Ответ: -2; 0,6.
47. ![]() Ответ:
Ответ: ![]() .
.
48. ![]() Ответ: -4; -3,5; -2; -1.
Ответ: -4; -3,5; -2; -1.
49. ![]() Ответ:
-0,2; 0,5; 1; 3.
Ответ:
-0,2; 0,5; 1; 3.
50. ![]() Ответ:
-2; 0,6.
Ответ:
-2; 0,6.
Решить системы уравнений
1.  Ответ:
Ответ:
![]() .
.
2. 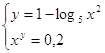 Ответ:
(5;-1).
Ответ:
(5;-1).
3. 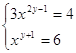 Ответ:
Ответ:
![]() .
.
4. 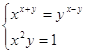 Ответ:
Ответ:
![]() .
.
5.  Ответ:
Ответ:
![]() .
.
6. 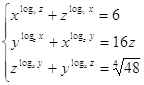 Ответ:
Ответ: ![]() .
.
7. 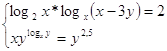 Ответ:
Ответ: ![]() .
.
8. 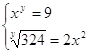 Ответ:
Ответ:
![]() .
.
9. 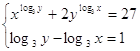 Ответ:
Ответ: ![]() .
.
10. 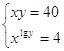 Ответ:
Ответ:
![]() .
.
11. 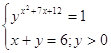
Ответ:
![]() .
.
12. 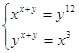 Ответ:
Ответ:
![]() .
.
13. 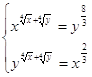
Ответ:
![]() .
.
14. 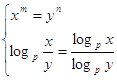
15. 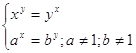
16. 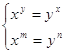
17. 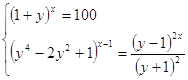
Ответ:
![]() .
.
18. 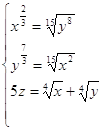
Ответ:
![]() .
.
19. 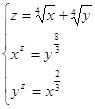
Ответ:
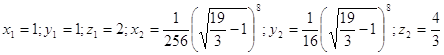 .
.
20. 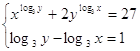 Ответ:
Ответ: ![]() .
.
21. 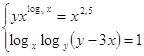 Ответ:
Ответ: ![]() .
.
22. 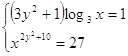 Ответ:
Ответ: ![]() .
.
23. 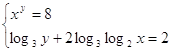 Ответ:
Ответ: ![]() .
.
Решить неравенства.
1. ![]()
Ответ:
если ![]() , то
, то ![]() если
если ![]() то
то ![]() .
.
2. ![]() Ответ:
Ответ: ![]() .
.
3. ![]() Ответ:
Ответ: ![]() .
.
4. ![]() Ответ:
Ответ:
![]() .
.
5. ![]() Ответ:
Ответ:
![]() .
.
6. ![]() Ответ:
Ответ:
![]() .
.
7. ![]() Ответ:
Ответ: ![]() .
.
8. ![]() Ответ:
Ответ: ![]() .
.
9. ![]() Ответ:
Ответ:
![]() .
.
10. ![]() Ответ:
Ответ: ![]() .
.
11. ![]() Ответ:
Ответ: ![]() .
.
12. ![]() Ответ:
Ответ: ![]() .
.
13. 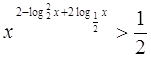 Ответ:
Ответ: ![]() .
.
14. 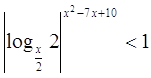 Ответ:
Ответ: ![]() .
.
15. ![]() Ответ:
Ответ: ![]() .
.
16. ![]() Ответ:
Ответ: ![]() .
.
17. ![]() Ответ:
Ответ: ![]() .
.
18. ![]() Ответ:
Ответ: ![]() .
.
19. 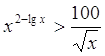 Ответ:
Ответ: ![]() .
.
20. ![]() Ответ:
Ответ: ![]() .
.
21. ![]() Ответ:
Ответ: ![]() .
.
Заключение.
Подводя итоги данного дипломного исследования, можно сделать следующие выводы:
1. Показательно-степенные уравнения и неравенства представляют интерес для их изучения и использования в курсах школьной математики и элементарной математики в ВУЗе. Между тем, почти во всех пособиях они, если и рассматриваются, то не полно или не точно.
2. Для этого вида уравнений и неравенств может быть предложен алгоритм решения. Наибольшие трудности могут встретиться при решении показательно-степенных уравнений и неравенств в случае, когда основание степени отрицательно.
3. Проведенные по теме: «Показательно-степенные уравнения и неравенства» на уроках и факультативных занятия в школе показали доступность этой темы для учеников, интересующихся математикой. Для таких занятий изготовлен задачник, содержащий более 70 показательно-степенных уравнений и неравенств.
Мое предложение – больше уделять времени решению показательно-степенных уравнений и неравенств, т.к. это поможет учащимся успешно сдать ЕГЭ и вступительные экзамены в ВУЗы.
Материал, приведенный в данной работе может служить методическим пособием в работе с учащимися на уроках и факультативах.
Список используемой литературы.
1. Авербух Б.Г., Рубинштейн А.И. Об определении степени и решении уравнений и неравенств, содержащих показательно степенную функцию.//Математика в школе. – 1996.-№2.-с.29-33.
2. Алгебра и начала анализа: Учебник для 10-11 классов общеобразовательных учреждений: Колмагоров А.Н., Абрамов А.М., Дудинцын Ю.П. и др.; Под редакцией Колмагорова А.Н. – 12-е изд. – М.: Просвещение, 2002.
3. Белоненко Т.В., Васильев А.Е., Васильева Н.И., Крымская .Д. Сборник конкурсных задач по математике. – СПб.: Спецлитература, 1997.
4. Василенко Ю.К. Тождества, уравнения, неравенства: Пособие для повышения квалификации учителей математики. – Белаидит. Белгород, 2003.
5. Василюк Л.И., Куваева Л.А. Математика для абитуриентов: Справочник в экзаменационных вопросах и ответах. – Мн. Амалфея, 1999.
6. Давыденко И.О. Пособие по математике. Для поступающих в высшие учебные заведения (с анализом ошибок абитуриентов).- 2-е изд. – Томск,из-во Томского университета, 1973.
7. Дорофеев Г.В., Потапов М.К., Розов Н.Х. Математика для поступающих в ВУЗы. – М.: Дрофа, 2000.
8. Дудинцын Ю.П., Смирнова В.К. Содержание и анализ письменных экзаменационных работ по алгебре и началам анализа: Пособие для учителя. – М.: Просвещение, 1995.
9. Единый государственный экзамен: Математика: Контрольно-измерительные материалы./ Денищева Л.О., Бойченко Е.М., Глазков6 под редакцией Ковалевой Г.С; М-во образования Российской Федерацию – М.: Просвещение, 2003.
10. Крамор В.С. Повторяем и систематизируем школьный курс алгебры и начал анализа. – 2-е изд. - М.: Просвещение, 1993.
11. Кутасов А.Д., Пиголкина Т.С., Чехлов В.И., Яковлева Т.Х.; под редакцией Яковлева Г.Н.. Пособие по математике для поступающих в ВУЗы.- 2-е изд.- М.: Наука, 1985.
12. Математика. Методические указания по подготовке к вступительным экзаменам./ СПбГИТМО. – СПб., 2000.
13. Нараленков М.И. Вступительные экзамены по математике. Алгебра: как решать задачи: Учебно-практическое пособие. – М.: Экзамен, 2003.
14. Норин А.В. Сборник задач по математике для поступающих в ВУЗы: Учебное пособие. – Спб.: Питер, 2003.
15. Потапов М.К., Олейник С.Н., Нестеренко Ю.В. Конкурсные задачи по математике: Справочное пособие. – 2-е изд. – М.: Физмалит, 2001.
16. Потапов М.К., Александров А.В., Пасиченко П.И. Алгебра и начала анализа. Современный курс для поступающих в ВУЗы. – М.: Экзамен, 1998.
17. Сборник задач по математике для поступающих в ВУЗы./ Под ред. Проф. Прилепко А.И. – М.: Высшая школа, 1983.
18. Симонов А.Я., Бакаев Д.С., Элельман А.Г. Система тренировочных задач и упражнений по математике. – М.: Просвещение, 1991.
19. Сканави М.И. Сборник задач по математике для поступающих в ВУЗы. - М.: Просвещение, 1988.
20. Цыпкин А.Г., Пинский А.И. Справочник пособие по методам решения задач по математике для средней школы. – М.: Наука. ГРФМЛ, 1984.
21. Черкасов О.Ю., Якушев А.Г. Математика. Интенсивный курс подготовки к экзаменам. – М.: Рольф, 1997.
22. Шарыгин И.Ф. Математика. Для поступающих в ВУЗы: Учебное пособие. – 4-е изд. –М.: Дрофа, 2002.
23. Шарыгин И.Ф., Голубев В.И. Решение задач: Учебное пособие для 11 класса общеобразовательных учреждений. – 2-е изд. – М.: Просвещение, 1995.
24. Шахно К.У. Сборник задач по элементарной математике повышенной трудности: Высшая школа, 1967.
25. Якушева Е.В., Попов А.В., Черкасов О.Ю., Якушев А.Г. Экзаменационные вопросы и ответы. Алгебра и начало анализа 9 и 11 выпускные классы: Учебное пособие.- М.: АСТ-Пресс, 2000.
Похожие работы
... проведении исследования были решены следующие задачи: 1) Проанализированы действующие учебники алгебры и начала математического анализа для выявления представленной в них методики решения иррациональных уравнений и неравенств. Проведенный анализ позволяет сделать следующие выводы: ·в средней школе недостаточное внимание уделяется методам решения различных иррациональных уравнений, в основном ...
... неравенств в школьном курсе не рассматри- вают, а на вступительных экзаменах эти задания часто дают. Я самостоятельно изучил правила решения иррациональных уравнений и неравенств. В реферате показаны решения как иррациональных уравнений и неравенств стандартного типа, так и повышенной сложности. Поэтому реферат можно использовать как учебное пособие для подготовки в ВУЗ, также рефератом можно ...
... сформулированной гипотезы необходимо было решить следующие задачи: 1. Выявить роль тригонометрических уравнений и неравенств при обучении математике; 2. Разработать методику формирования умений решать тригонометрические уравнения и неравенства, направленную на развитие тригонометрических представлений; 3. Экспериментально проверить эффективность разработанной методики. Для решения ...
... курс «Решение уравнений и неравенств с использованием свойств функций» Глава II. Разработка элективного курса «Решение уравнений и неравенств с использованием свойств функций» §1. Методические основы разработки элективного курса Пояснительная записка. Основная задача обучения математике в школе – обеспечить прочное и сознательное овладение учащимися системой математических знаний и ...
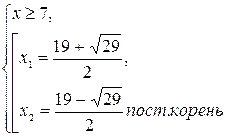


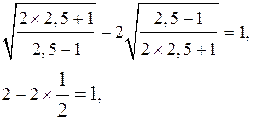
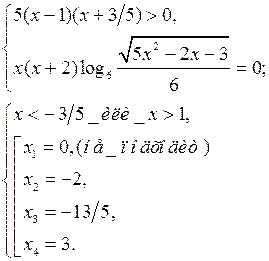





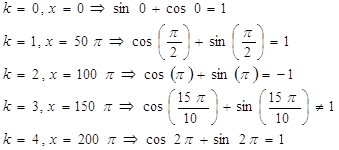
0 комментариев