Навигация
Нахождение пределов функций
Контрольная работа по дисциплине «Математика»
для студентов заочного отделения
1. Найти пределы функций:
а) ![]() =;
=; 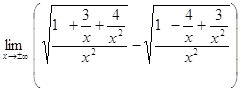 =
=
= 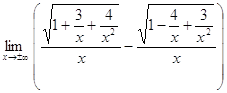 =
= 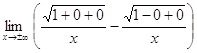 =
=
= ![]() =
= ![]() =
= ![]() = 0;
= 0;
б) 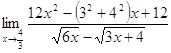 =
= 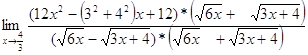 =
=
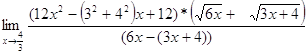 =
=
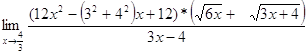 =
=
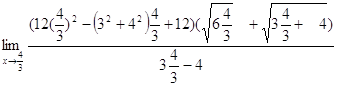 =
= 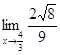 =
= ![]() =.6290;
=.6290;
в) ![]() =
= 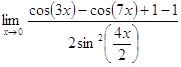 =
=
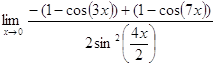 =
= 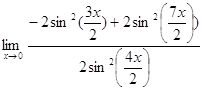 =
= ![]() = 0;
= 0;
г) ![]() =
= ![]() =
= 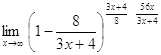 =
= ![]() =
=
= ln ![]() =
= 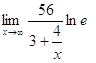 = ln e*
= ln e*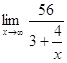 = 1*56/3 = 18.667;
= 1*56/3 = 18.667;
д) ![]() ;
; ![]() =
= ![]() =
=
= ![]() =
= ![]() ;
;![]() ;
;
е) ![]() =
= ![]() =
= 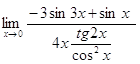 =
=
= ![]() =
= ![]() +
+ ![]() =
=
= 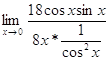 -
- 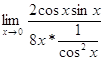 =
= ![]() -
- ![]() =
=
= ![]() = 2.
= 2.
2. Найти производные ![]() функций:
функций:
а) 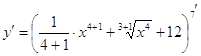 =
= ![]() =
=
= ![]() ;
;
б) ![]() =
= ![]() =
= ![]() =
= ![]() ;
;
в) 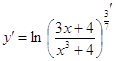 =
= 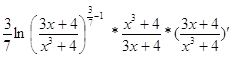 =
=
= 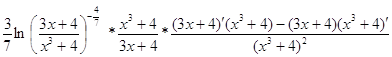 =
=
= 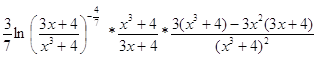 =
=
= 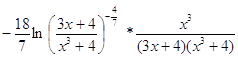 ;
;
г) ![]() =
=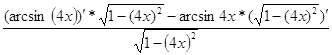 =
=
= 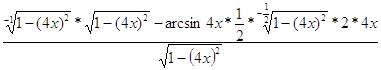 =
=
= 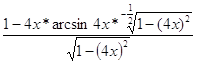 =
= 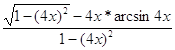 ;
;
д) ![]() =
= ![]() ;
;
е) ![]() ;
; ![]() ;
;
![]() ;
;![]()
ж) 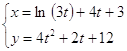 ;
;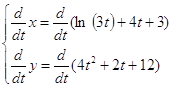 ;
; 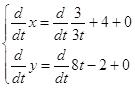 ;
;
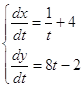 ;
; 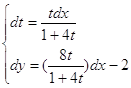 ;
;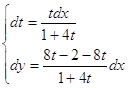 ;
; 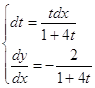 ;
;![]() ;
;
з) ![]() .
.![]() =
= ![]() =
=
= ![]() =
= ![]() ;
;
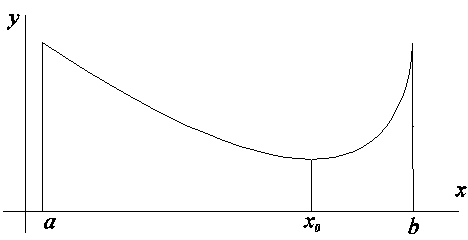
3. С помощью методов дифференциального исчисления построить график функции
![]() .
.
1 Знаменатель положительный не для всех значений Х, область определения функции имеет точку разрыва. ![]() отсюда IхI=7 или точки разрыва х = -7 и х=7.
отсюда IхI=7 или точки разрыва х = -7 и х=7.
Похожие работы
... функции в точке перегиба равна нулю, то есть = 0. Если вторая производная при переходе через некоторую точку меняет свой знак, то является точка перегиба ее графика. При исследовании функции и построении ее графика рекомендуется использовать следующую схему: Найти область определения функции. Исследовать функции на четность – нечетность (если функция четная или нечетная, то график ...
ывают определением на «языке последовательностей». Второе определение носит название «на языке ». Кроме понятия предела функции в точке, существует также понятие предела функции при стремлении аргумента к бесконечности: число А называется пределом функции при , если для любого числа существует такое число d, что при всех справедливо неравенство : . Теоремы о пределах функций являются базой для ...
... типов неопределенностей. Примеры для этого и последующего раздела были взяты из [Марон]. В четвертом разделе приведен вывод формулы Тейлора и показано применение формулы Тейлора для нахождения эквивалентных функций и вычисления пределов. 1. Бесконечно малые и их сравнения; символы "o малое" и "о большое" Определение. Бесконечно малой в x0 называется функция f (x) такая, что Свойства ...
... , что и ошибки эксперимента, то итерации надо прекращать. Поскольку вблизи минимума чаще всего ~, то небольшая погрешность функции приводит к появлению довольно большой области неопределенности ~. 2. Минимум функции многих переменных 2.1 Рельеф функции Основные трудности многомерного случая удобно рассмотреть на примере функции двух переменных . Она описывает некоторую поверхность в ...





0 комментариев