Навигация
Найти наибольшее и наименьшее значения функции при m=3, n=4
4640
знаков
3
таблицы
6
изображений
10. Найти наибольшее и наименьшее значения функции при m=3, n=4
в области, заданной неравенствами:
.
D=AC-B;
A=
B=
C=
D=AC-B=(
)(
) - 
;
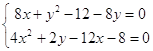
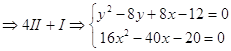
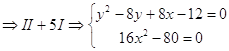
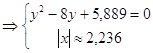
найдем
; 
Получим четыре точки: 1) (2,236:7,18), (1,236:0,82), (-2,236:7,18), (-2,236:0,82).
A=8+7,18*7,18-8*7,18=2,11 > 0;
= -114,74 < 0 – нет экстремума функции,
= 45097,12 > 0 – min функции 
= 12,279;
= 1767.38 > 0 - min функции = 65,94;
= -160,296 < 0 – нет экстремума функции.
11. Изменить порядок интегрирования при m=3, n=4:
.
= 
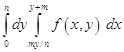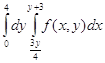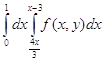, так как 
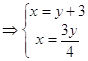
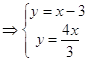
подставляя x = 0 x = 4 в последние уравнения получим
.
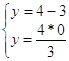
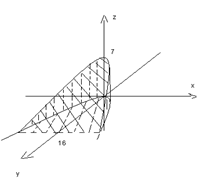
12. Сделать чертеж и найти объем тела, ограниченного поверхностями 
, 
и плоскостью, проходящей через точки 
, 
и 
.
А)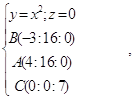
см. рис.
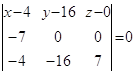
- получим уравнение плоскости, через которую проходят точки А, В и С.
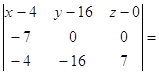7(х-4)+7*16*(z-0)-(y-16)*4+4(z-0)+49(y-16)+16(x-4)=
23x-812+116z-45y=0
Получим пределы интегрирования:
Для z – от 0 до z=7-0,198x+0,388y. Для у – от 0 до у=х^2. Для х – от 0 до х=76,81(объем фигуры разбиваем пополам).
= 
=
=
= 
=
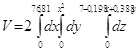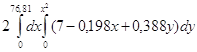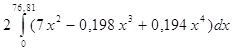=232,109 куб.ед.,
13. Вычислить при m=3, n=4 
, где 
, 
, а контур 
образован линиями 
, 
, 
.
а) непосредственно;
б) по формулам Грина.
,
P(x,y) = 4y+2x, Q(x,y) = 3x+2y, и контур С образован линиями 16y = 9x^3, y = 9, x = 0.
= 
=
= 
=
= 
=
= 
=
= 
=
= 
=
= 
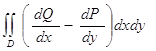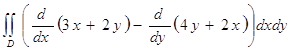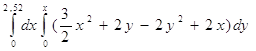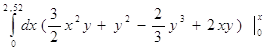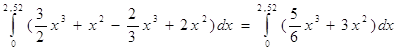=32,4060912,
где пределы интегрирования были получены:
и у = 9, то 
откуда х = 
2,52.
14. Даны поле 
и пирамида с вершинами 
, 
, 
,. Найти при m=3, n=4:
O(0:0:0), A(3:0:0), B(0:4:0), C(0:0:7).
а) поток поля 
через грань 
пирамиды в направлении нормали, составляющей острый угол с осью 
;
=
= 
=
=
=
=
=
=
=…
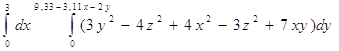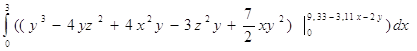после подстановки и преобразования однородных членов получим:
… = 8423,43 - 3336,03*у - 293,9*z^2 +118,98*у^2 – 24y^3 + 42y*z^2, т.е.
поток поля
= 8423,43 - 3336,03*у - 293,9*z^2 +118,98*у^2 – 24y^3 + 42y*z^2.
б) поток поля через внешнюю поверхность пирамиды с помощью теоремы Остроградского – Гаусса;
в) циркуляцию поля вдоль замкнутого контура ;
с помощью теоремы Стока (обход контура происходит в положительном направлении относительно внешней нормали к поверхности пирамиды).
rot(F) = 
,
в нашем случае 
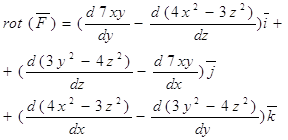
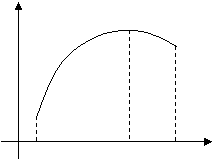
15. Найти первообразные и вычислить значение определенного интеграла:
= 
.
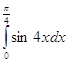Похожие работы
... функции в точке перегиба равна нулю, то есть = 0. Если вторая производная при переходе через некоторую точку меняет свой знак, то является точка перегиба ее графика. При исследовании функции и построении ее графика рекомендуется использовать следующую схему: Найти область определения функции. Исследовать функции на четность – нечетность (если функция четная или нечетная, то график ...
ывают определением на «языке последовательностей». Второе определение носит название «на языке ». Кроме понятия предела функции в точке, существует также понятие предела функции при стремлении аргумента к бесконечности: число А называется пределом функции при , если для любого числа существует такое число d, что при всех справедливо неравенство : . Теоремы о пределах функций являются базой для ...
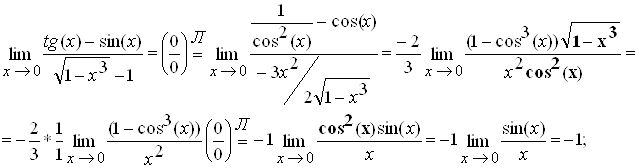
... типов неопределенностей. Примеры для этого и последующего раздела были взяты из [Марон]. В четвертом разделе приведен вывод формулы Тейлора и показано применение формулы Тейлора для нахождения эквивалентных функций и вычисления пределов. 1. Бесконечно малые и их сравнения; символы "o малое" и "о большое" Определение. Бесконечно малой в x0 называется функция f (x) такая, что Свойства ...
... , что и ошибки эксперимента, то итерации надо прекращать. Поскольку вблизи минимума чаще всего ~, то небольшая погрешность функции приводит к появлению довольно большой области неопределенности ~. 2. Минимум функции многих переменных 2.1 Рельеф функции Основные трудности многомерного случая удобно рассмотреть на примере функции двух переменных . Она описывает некоторую поверхность в ...
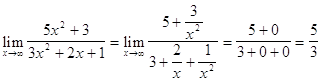
0 комментариев