Навигация
2.1 Выбор варианта задания
Вариант требующего минимизации выражения бинарного отношения образуется заданием и подстановкой для шаблонной формулы: набора операций над действительными числами; набора нетривиальных операндов; бинарного отношения.
«№операций» =9mod4+1=2
| №операц | a | b | g | d |
| Вариант2 | abs | - | Æ | * |
«№операндов»=9mod7+1=3
| №операн | оп-д1 | оп-д2 | оп-д3 | оп-д4 |
| Вариант3 | b-a | 5*a | 2*a+b | a/2 |
«№отношения»=24mod5+1=5
| №варианта | отношение |
| Варіант 5 | = |
2.2 Бинарное отношение
В шаблонную формулу
( (Оп1 Оп2)) Relation ( (Оп3 Оп4))
подставляются результаты, и получается:
(abs((b-a-5*a)) = (Æ((2*a+b)*a/2)
упрощение формулы :
| b – a – 5a | = ( 2a + b ) a/2
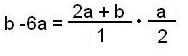
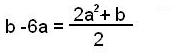
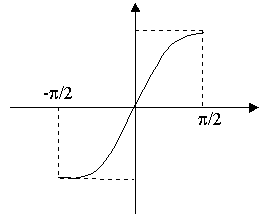
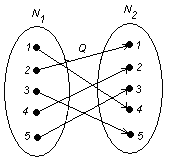
2.3 Построение графика
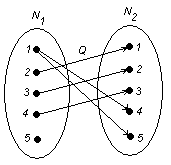
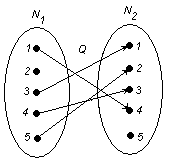
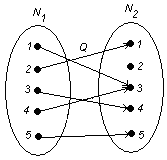
По данному отношению с помощью программ MathCad или MathLab, или же от руки, можно построить график:
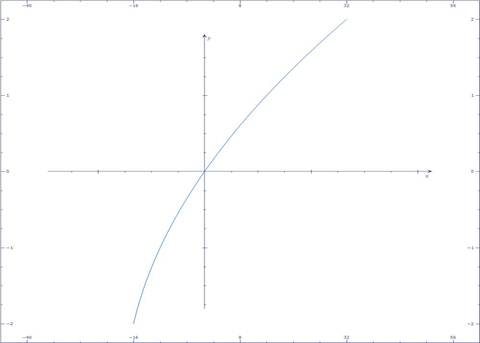
2.4 Исследование свойств отношения
Свойства отношений доказываются путём приведения примеров на графике:
1. Функционален, так как не содержит пары с одинаковыми первыми коэфициентами
2. Инъективен, так как не содержит пары с одинаковыми вторыми компонентами «b» и разными первыми компонентами «a».
3. Не всюду определен, так как область определения не совпадает с областью отправления
4. Сюрьективен так как его область значений равна области прибытия.
5. Биективен, так как функционален, инъективен и сюрьективен.
6. Не рефлексивен так как график не содержит прямую в = а.
7. Актирефлексивен так как график содержит точки , лежащие на прямой и = а.
8. Не иррефлексивен, так как найдутся точки, принадлежащие графику и лежащие на прямой в = а .
9. Не симметричен, так как найдутся точки, не принадлежащие графику и симметричные относительно прямой в = а.
10. Не анттисимметричен, так как найдутся точки, принадлежащие графику и не симметричные относительно прямой в = а.
11. Не ассиметричен, так как найдутся точки, принадлежащие графику и симметричные относительно прямой в = а, и одновременно найдутся точки, не принадлежащие графику и симметричные относительно прямой в = а.
12. Не транзитивен.
Свойства отношения внесены в таблицу
| Функциональность | + |
| Инъективность | + |
| Всюду определенность | – |
| Сюръективность | + |
| Биективность | + |
| Рефлексивность | – |
| Не рефлексивность | – |
| Антирефлексивность | + |
| Симметричность | – |
| Асимметричность | – |
| Антисимметричность | – |
| Транзитивность | – |
Задание № 3
Анализ заданной в определенном функциональном базисе логической схемыВариант исходной логической схемы образуется заданием функционального базиса логических функций, размещением логических элементов в сетке мест графического изображения логической схемы, списком связей входов и выходов логических элементов.
Номер варианта заданного функционального базиса логических функций {№Ф-ции1,№Ф-ции2,№Ф-ции3} из таблицы 6, обозначаемый как «№Базиса», получается следующим образом:
«№Базиса»=(«№Зачетки»%8)+1
где % - операция получения целочисленного остатка от деления.
«№Базиса»=(9%8)+1=2, т.е. из таблицы 6 следует, что
{№Ф-ции1,№Ф-ции2,№Ф-ции3}={2,9,14}
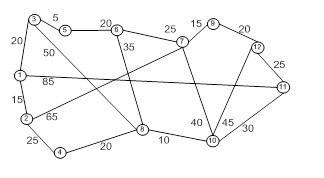
Графическое изображение логической схемы содержит пятнадцать мест для размещения (три ряда по пять элементов) логических элементов, реализующих логические функции базиса. Элементы пронумерованы с 5 по 19 включительно, номера с 1 по 4 принадлежат входам логической схемы, а номер 20 приписан выходу всей схемы.
Номер варианта размещения логических элементов в сетке мест графического изображения логической схемы из таблицы 7, обозначаемый как «№Размещения» получается следующим образом:
«№Размещения»= («№Зачетки»%3)+1
где % - операция получения целочисленного остатка от деления.
«№Размещения»=(9%3)+1=1, т.е из таблицы 7 получаем следующее расположение для базиса {№Ф-ции1,№Ф-ции2,№Ф-ции3}={4,6,8 }:
| №элем №вар | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| ф-я1 | x | x | x | x | x | ||||||||||
| ф-я2 | x | x | x | x | x | ||||||||||
| ф-я3 | x | x | x | x | x |
Номер варианта списка связей входов и выходов логических элементов логической схемы обозначаемый как «№Связей» получается следующим образом:
«№Связей»=(«№Зачетки»%13)+1
где % - операция получения целочисленного остатка от деления.
«№Связей»=(9%13)+1=10
В списке связей для каждого логического элемента указаны номера логических элементов, выходы которых соединены с его входами.
Для данного варианта список связей выглядит следующим образом:
5(1,2); 6(1,2); 7(3,4,6); 8(5,6,7); 9(4,6); 10(4,7); 11(1,8,10); 12(1,9); 13(9,10); 14(9,11); 15(10,12,14); 16(10,13); 17(11,14); 18(15,17); 19(16,18); 20(18).
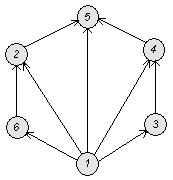
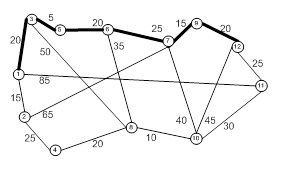
Полученная схема приведена ниже:
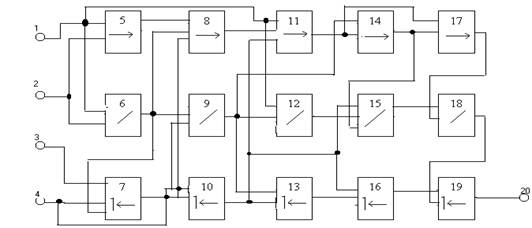
Анализ схемы.
Анализ схемы выполняется путем поэтапной подстановки выражений для реализации y
y5=x1~x2=ùx1ùx2+x1x2
y6=x1/x2=ùx1+ùx2
y7=x3ù→x4ù→y6=(x3ùx4) ù→y6=x3x4x1x2=x1x2x3x4
y8=y5~y6~y7=((x1+x2)( ùx1+ùx2)x1x2+(ùx1ùx2+x1x2)( ùx1+ùx2)) ~y7=
=(ùx1ùx2) ~y7=(x1+x2)( ùx1+ùx2+ùx3+ùx4)+( ùx1ùx2)x1x2x3x4=x1ùx2+x1ùx3+
+x1ùx4+ùx1x2+x2ùx3+x2ùx4
y9=x4/y6 =ùx4+x1x2
y10=x4ù→y7=x4(ùx1+ùx2+ùx3+ùx4)= ùx1x4+ùx2x4+ùx3x4
y11=x1~y8~y10=( ùx1(ùx1+x2)( ùx1+x3)( ùx1+x4)(x1+ùx2)( ùx2+x3)( ùx2+x4)+
+x1(x1ùx2+x1ùx3+x1ùx4+ùx1x2+x2ùx3+x2ùx4)) ~y10=((ùx1+ùx1x2) (ùx1+x3) (ùx1+x4)(x1+ùx2)( ùx2+x3)( ùx2+x4)+(x1ùx2+x1ùx3+x1ùx4+x1x2ùx3+x1x2ùx4)) ~y10=(ùx1ùx2(ùx1+x3)( ùx2+x3)( ùx2+x4)( ùx1+x4)+ (x1ùx2+x1ùx3+x1ùx4+ +x1x2ùx3+x1x2ùx4)) ~y10=((ùx1ùx2+ùx1ùx2x3) (ùx2+x3)( ùx2+x4)( ùx1+x4)+
+(x1ùx2+x1ùx3+x1ùx4+ +x1x2ùx3+x1x2ùx4)) ~y10=((ùx1ùx2+ùx1ùx2x3)
( ùx2+x4)( ùx1+x4)+ (x1ùx2+x1ùx3+x1ùx4+ x1x2ùx3+x1x2ùx4)) ~y10=
=((ùx1ùx2+ùx1ùx2x4+ùx1ùx2x3+ùx1ùx2x3x4)( ùx1+x4)+( x1ùx2+x1ùx3+
+ x1ùx4+ x1x2ùx3+x1x2ùx4)) ~y10=(ùx1ùx2+ùx1ùx2x4+ùx1ùx2x3x4+
+ x1ùx2+x1ùx3+ x1ùx4+ x1x2ùx3+x1x2ùx4)~y10=(ùx1ùx2+x1ùx2+x1ùx3+
+x1ùx4+x1x2ùx3+x1x2ùx4) ~y10=(ùx2+x1ùx3+x1ùx4+x1x2ùx3+x1x2ùx4) ~y10=
=(ùx2+x1ùx3+x1ùx4)~y10=x2(ùx1+x3)( ùx1+x4)(x1+ùx4)(x2+ùx4)(x3+ùx4)+
+(ùx2+x1ùx3+x1ùx4)( ùx1x4+ùx2x4+ùx3x4)=x2(ùx1+x3)( ùx1ùx4+x1x4)
(x2+ùx4)(x3+ùx4) +(ùx2+x1ùx3+x1ùx4)( ùx1x4+ùx2x4+ùx3x4)=
=x2(ùx1+x3)( ùx1x2ùx4+x1x2x4+ùx1ùx4)(x3+ùx4) +(ùx2+x1ùx3+x1ùx4)
( ùx1x4+ùx2x4+ùx3x4)=x2(ùx1+x3)( ùx1x2x3ùx4+x1x2x3x4+ùx1x2x4+
+ùx1x2ùx4) +(ùx2+x1ùx3+x1ùx4)( ùx1x4+ùx2x4+ùx3x4)=( ùx1+x3)( ùx1x2x4+
+x1x2x3x4+ùx1x2x3x4) +(ùx2+x1ùx3+x1ùx4)( ùx1x4+ùx2x4+ùx3x4)=
=(ùx1+x3) (ùx1x2x4+x1x2x3x4) +(ùx2+x1ùx3+x1ùx4)( ùx1x4+ùx2x4+ùx3x4)=
=ùx1x2x4+ùx1x2x3x4+x1x2x3x4+ùx1ùx2x4+ùx2x4+ùx2ùx3x4+x1ùx2ùx3x4+
+x1ùx3x4=ùx1x2x3+x1x2x3x4+ùx2x4+x1ùx3x4
y12=x1/y9 =ùx1+x4(ùx1+ùx2)= ùx1+ùx1x4+ùx2x4=x1+ùx2x4
y13= y9ù→y10=(ùx4+x1x2)(x1+ùx4)(x2+ùx4)(x3+ùx4)=(x1ùx4+ùx4+x1x2+
+x1x2ùx4)(x2+ùx4)(x3+ùx4)=( ùx4+x1x2)(x2+ùx4)(x3+ùx4)=(x2ùx4+ùx4+
+x1x2+x1x2ùx4)(x3+ùx4)=( ùx4+x1x2)(x3+ùx4)=x3ùx4+ùx4+x1x2x3+
+x1x2ùx4=ùx4+x1x2x3
y14=y9~y11 =x4(ùx1+ùx2)(x1+ùx2+ùx4)( ùx1+ùx2+ùx3+ùx4)(x2+ùx4)
(ùx1+x3+ùx4)+( ùx4+x1x2)( ùx1x2x4+x1x2x3x4+ùx2x4+x1ùx3x4)=
=x4(ùx1ùx2+ùx1ùx4+x1ùx2+ùx2)( ùx1+ùx2+ùx3+ùx4)(x2+ùx4)( ùx1+x3+ùx4)+
+( ùx4+x1x2)( ùx1x2x4+x1x2x3x4+ùx2x4+x1ùx3x4)=x4(ùx2+ùx1ùx4)( ùx1+ùx2+
+ùx3+ùx4)( ùx1x2+x2x3+x2ùx4+ùx1ùx4+ùx3ùx4+ùx4) +( ùx4+x1x2)( ùx1x2x4+
+ x1x2x3x4+ùx2x4+x1ùx3x4)= ùx2x4(ùx1+ùx2+ùx3+ùx4)( ùx1x2+x2x3+ùx4)+
+( ùx4+x1x2)( ùx1x2x4+x1x2x3x4+ùx2x4+x1ùx3x4)=( ùx1ùx2x4+ùx2x4+
+ùx2ùx3x4)( ùx1x2+x2x3+ùx4)+ ( ùx4+x1x2) (ùx1x2x4+x1x2x3x4+ùx2x4+
+x1ùx3x4)= ùx2x4(ùx1x2+x2x3+ùx4) +( ùx4+x1x2)( ùx1x2x4 +x1x2x3x4+ùx2x4+
x1ùx3x4)=( ùx4+x1x2)( ùx1x2x4+x1x2x3x4+ùx2x4+x1ùx3x4)=x1x2x3x4+
+x1x2ùx3x4=x1x2x4
y15=y10/y12/y14=((x1+ùx4)(x2+ùx4)(x3+ùx4)+x1(x2+ùx4))/y14=
=((x1x2+x1ùx4+x2ùx4+ùx4)+x1x2+x1ùx4)/y14=((x1x2x3+x1x2ùx4+x3ùx4+ùx4)+
+x1x2+x1ùx4)/y14=(x1x2+ùx4)/y14=(ùx1+ùx2)x4+(ùx1+ùx2+ùx4)=
=ùx1x4+ùx2x4+ùx1+ùx2+ùx4=ùx1+ùx2+ùx4
y16=y10ù→y13=(ùx1x4+ùx2x4+ùx3x4)x4(ùx1+ùx2+ùx3)= ùx1x4+ùx1ùx2x4+
+ùx1ùx3x4+ùx2x4+ùx1ùx2x4+ùx1ùx3x4+ùx3x4+ùx1ùx3x4+ùx2ùx3x4=
=ùx1x4+ùx2x4+ùx3x4
y17=y11~y14=(x1+ùx2+x4)( ùx1+ùx2+ùx3+ùx4)(x2+ùx4)( ùx1+x3+ùx4)
(ùx1+ùx2+ùx4)+( ùx1x2x4+x1x2x3x4+ùx2x4+x1ùx3x4)x1x2x4=
=(x1ùx2+x1ùx3+x1ùx4+ùx1ùx2+ùx2+ùx2ùx3+ùx2ùx4+ùx1x4+ùx2x4+ùx3x4)
(ùx1x2+x2x3+x2ùx4+ùx1ùx4+x3ùx4+ùx4)+x1x2x3x4+x1x2ùx3x4=
=ùx2ùx4+x1ùx3ùx4+x1x2x3ùx4+x1ùx4+ùx1x2x4+ùx1x2x3x4+ùx1x2ùx3x4+
+x1x2x3x4+x1x2ùx3x4=ùx2ùx4+x1ùx4+ùx1x2x4+ùx1x2x3x4+ùx1x2ùx3x4+
+x2x4=ùx2ùx4+x1ùx4+x2x4
y18=y15/y17=x1x2x4+(x2+x4)( ùx1+x4)( ùx2+ùx4)=x1x2x4+(ùx1x2+x2x4+
+ùx1x4+x4)( ùx2+ùx4)=x1x2x4+(ùx1x2+x4)( ùx2+ùx4)=x1x2x4+ùx1x2ùx4+
+ùx2x4=ùx1x2ùx4+x1x4+ùx2x4
y19=y16ù→y18 =(ùx1x4+ùx2x4+ùx3x4)( ùx1+ùx2+ùx4)(x1+ùx2+x4)(x2+ùx4)=
=(ùx1x4+ùx2x4+ùx3x4)( ùx1+ùx2+ùx4)(x1x2+x1ùx4+ùx2ùx4+x2x4)=
=(ùx1x4+ùx2x4+ùx3x4)( ùx1ùx2ùx4+ùx1x2x4+x1ùx2ùx4+ùx2ùx4+x1x2ùx4+
+x1ùx4+ùx2ùx4)= (ùx1x4+ùx2x4+ùx3x4)( ùx1x2x4+ùx2ùx4+x1ùx4)=
=ùx1x2x4+ùx1x2ùx3x4=ùx1x2x4
y20=y18=ùx1x2ùx4+x1x4+ùx2x4
Теперь выполним построение сводной таблицы. В левой части таблицы приводятся все возможные наборы из четырех аргументов – от нулевого до пятнадцатого, а в правой – значения функции для каждого элемента логической схемы.
| x1 | x2 | x3 | x4 | y5 | y6 | y7 | y8 | y9 | y10 | y11 | y12 | y13 | y14 | y15 | y16 | y17 | y18 | y19 | y20 |
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
Формула ùx1x2ùx4+x1x4+ùx2x4 , полученная для всей таблицы, записана в виде ДНФ. Для перевода ее в СДНФ, введем единицы для недостающих элементов в каждый минитерм:
СДНФ=(x3+ùx3)(x2+ùx2) x1x4+(x3+ùx3) ùx1x2ùx4+(x3+ùx3)(x1+ùx1)ùx2x4=
=x1x2x3x4+x1x2ùx3x4+ùx1x2x3ùx4+ùx1x2ùx3ùx4+x1ùx2x3x4+x1ùx2ùx3x4+
+ùx1ùx2x3x4+ùx1ùx2ùx3x4
Выполним перевод из CДНФ в CКНФ:
CКНФ=(ùx1+ùx2+ùx3+ùx4)( ùx1+ùx2+x3+ùx4)(x1+ùx2+ùx3+x4)(x1+ùx2+x3+x4)
(ùx1+x2+ùx3+ùx4)( ùx1+x2+x3+ùx4)(x1+x2+ùx3+ùx4)(x1+x2+x3+ùx4)
Задание № 4
Минимизация методами Квайна-МакКласки и Петрика, а также с помощью карт Карно булевой функции по исходной таблице истинности, полученной в п.4 Метод Квайна-Мак-КласкиРассмотрим функцию четырех переменных Q=f(x1,x2,x3,x4) заданную таблицей 2.
Ей соответствует дизъюнктивная совершенная нормальная форма
x1x2x3x4+x1x2ùx3x4+ùx1x2x3ùx4+ùx1x2ùx3ùx4+x1ùx2x3x4+x1ùx2ùx3x4+
+ùx1ùx2x3x4+ùx1ùx2ùx3x4
Множество 0-Кубов после разбиения и упорядочивания записывается следующим образом:
| 0001 0100 |
| 0110 1001 0011 |
| 1101 1011 |
| 1111 |
K0=
Будем попарно сравнивать S-кубы из соседних поясов, склеивая таковые, отличающиеся только по одной координате. Такая операция склеивания соответствует объединению двух S-кубов. Получим (S+1)-куб, в котором склеиваемую координату заместим символом «~». Склеиваемые кубы будем отмечать знаком «ü».
| 0001ü 0100ü |
| 0110ü 1001ü 0011ü |
| 1101ü 1011ü |
| 1111ü |
K’0=
| ~001ü 00~1ü 01~0 |
| 1~01ü 10~1ü ~011ü |
| 11~1ü 1~11ü |
K1 =
K
| ~0~1 |
| 1~~1 |
K2 =
K3= Æ
Очевидно, во множестве K2 склеивание S-кубов невозможно. Поэтому следующее множество K3 – пустое. Полученная сокращенная форма содержит четыре простые импликанты (неотмеченные кубы, то есть те, которые не склеились в процессе сравнения).
Теперь построим таблицу Квайна. Ее строкам соответствуют простые импликанты из сокращенной формы, столбцам – конституэнты булевой функции.
| 0001 | 0100 | 0110 | 1001 | 0011 | 1101 | 1011 | 1111 | ||
| 01~0 | a | ü | ü | ||||||
| ~0~1 | b | ü | ü | ü | ü | ||||
| 1~~1 | c | ü | ü | ü | ü |
Очевидно, каждая импликанта является существенной. В этом случае тупиковая форма единственна. Она же будет являться и минимальной формой.
МДНФ=ùx1x2ùx4+x1x4+ùx2x4
Полученная формула в точности равна полученной еще на этапе анализа логической схемы. Действительно, при анализе мы пользовались аналитической минимизацией, применяя те ли иные свойства. Универсальный метод Квайна-Мак-Класки показал, что полученная ДНФ действительно является минимальной.
Полученный вывод можно подтвердить также с помощью метода Петрика. Логическое условие покрытия всей таблицы Квайна имеет вид:
bÙaÙaÙ(bÚc)ÙbÙcÙ(bÚc)Ùc
Производя простые преобразования, получаем:
aÚbÚc
Таким образом, с помощью метода Петрика получаем следующее выражение для МДНФ:
МДНФ=ùx1x2ùx4+x1x4+ùx2x4
Видим, что оно совпадает с выражением, полученным с помощью метода Квайна-Мак-Класки.
Теперь рассмотрим минимизацию методом карты Карно:
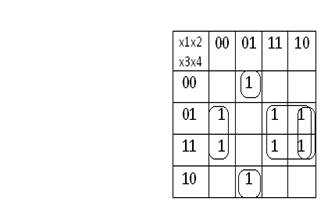
МДНФ=ùx1x2ùx4+x1x4+ùx2x4
Мы получили результат, который совпадает с двумя результатами, полученными раннее. Это говорит о правильности произведенных вычислений.
Минимизация методами Квайна-Мак-Класки и Петрика, а также с помощью карт Карно формулы частично определенной булевой функции, полученной из таблицы истинности п.4, пополненной заданными безразличными входными наборами.Выбор безразличных наборов
По построенной таблице истинности булевой функции заданной логической схемы строится таблица истинности частично определенной булевой функции выбором четырех случайно выбранных безразличных входных двоичных наборов, на которых частичная булева функция не определена (безразлична). В случае наложения безразличного набора на единичный набор (на котором функция принимает значение «1») для данного набора значений аргументов сохраняется значение функции, равное «1».
Номер варианта безразличных входных наборов частичной булевой функции {№Наб1, №Наб2, №Наб3, №Наб4} из таблицы 8, обозначаемый как «№Наборов», получается определением смещенного на «1» целочисленного остатка от деления «№Зачетки» на число «11»- число вариантов таблицы 8 по следующей формуле:
«№Наборов»= «№Зачетки»%9+1
где %- операция получения целочисленного остатка от деления.
«№Наборов»=(9 %11)+1=3, т.е. из таблицы 8 следует, что выбраны безразличные наборы {№Наб1, №Наб2, №Наб3, №Наб4}={8,10,11,12}=
={0111, 1001, 1010, 1011}.
Таким образом, понятно, что изменений не произойдет, так как все безразличные наборы уже присутствуют в наборах булевой функции, полученной из сводной таблицы. Значит вычисление минимизации для функции, пополненной безразличными наборами, даст результат, полученный раннее, т.е.
МДНФ= ùx1x2ùx4+x1x4+ùx2x4
Перевод полученных в пунктах 5 и 6 минимальных формул из булевого базиса в заданный функциональный базис.
Построим логическую схему для МДНФ:
МДНФ=ùx1x2ùx4+x1x4+ùx2x4
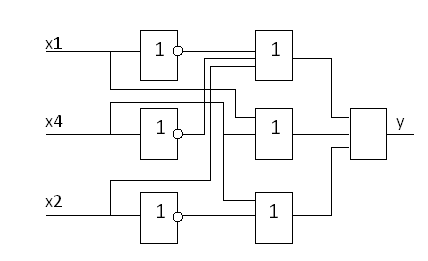
Преобразуем МДНФ из булевого базиса {Ú, Ù, ù} в заданный функциональный базис:
МДНФ=(((((x2ù→x4) ù→x1)/(x2ù→x4) ù→x1))/((x4ù→x2)/(x4ù→x2)))/
/(((x2ù→x4) ù→x1)/(x2ù→x4) ù→x1))/((x4ù→x2)/(x4ù→x2))))/(x1/x4)
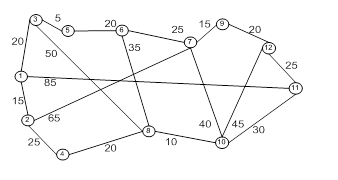
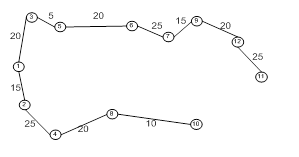
Логическая схема для полученной формулы булевой функции выглядит следующим образом:
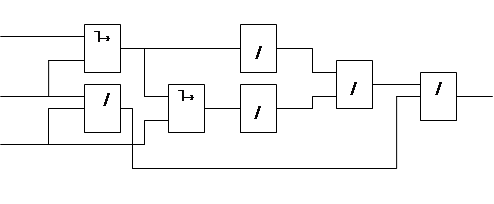
Выводы
В ходе выполнения расчетно-графической работы по дисциплине «Основы дискретной математики» были закреплены основные теоретические знания и практические навыки.
В процессе расчетно-графической работы для построенных в соответствии с индивидуальным вариантом множественной формулы, бинарного отношения и логической схемы выполнен анализ, минимизация множественных и булевых формул, перевод булевых формул в заданный базис и синтез схем в заданном базисе.
Литература:
1. Методические указания выполнения расчетно-графической работы по дисциплине «Основы дискретной математики» для студентов специальностей 6.0804 и 6.0915. / Сост. А. Н. Мартынюк. – Одесса: ОНПУ, 2002.
2. Конспект лекций по дисциплине «Основы дискретной математики» для студентов специальностей 6.0804 и 6.0915. / Сост. А. Н. Мартынюк. – Одесса: ОНПУ, 2002.
Похожие работы
... Е и множество и мы рассматриваем все его подмножества, то множество Е называется униварсельным. Пример: Если за Е взять множество книг то его подмножества: художественные книги, книги по математике, физики, физики … Если универсальное множество состоит из n элементов, то число подмножеств = 2n. Если , состоящее из элементов E, не принадлежащих А, называется дополненным. Множество можно задать: ...
в и формальных систем является центральной в дисциплине. В настоящие время от нее возникли ответвления, например, разработка алгоритмических языков программирования.Одной из важнейших проблем в дискретной математики является проблема сложности вычислений.Теория сложности вычислений помогает оценить расход времени и памяти при решении задач на ЭВМ. Теория сложности позволяет выделить объективно ...
... которой были разработаны в последней четверти 19 века Георгом Кантором. Цель контрольной работы – ознакомится с основными понятиями и методами решения по дискретной математике, уметь применить полученные знания при решении практического задания. Задание 1 Представить с помощью кругов Эйлера множественное выражение . Используя законы и свойства алгебры множеств, упростить заданное ...
элементы теории нечетких множеств можно применять для решения экономических задач в условиях неопределённости. 1. применение Логических функций 1.1 Применение методов дискретной математики в экономике При исследовании, анализе и решении управленческих проблем, моделировании объектов исследования и анализа широко используются методы формализированного представления, являющегося предметом ...
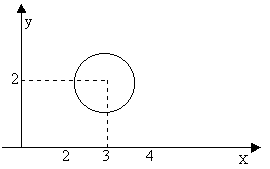
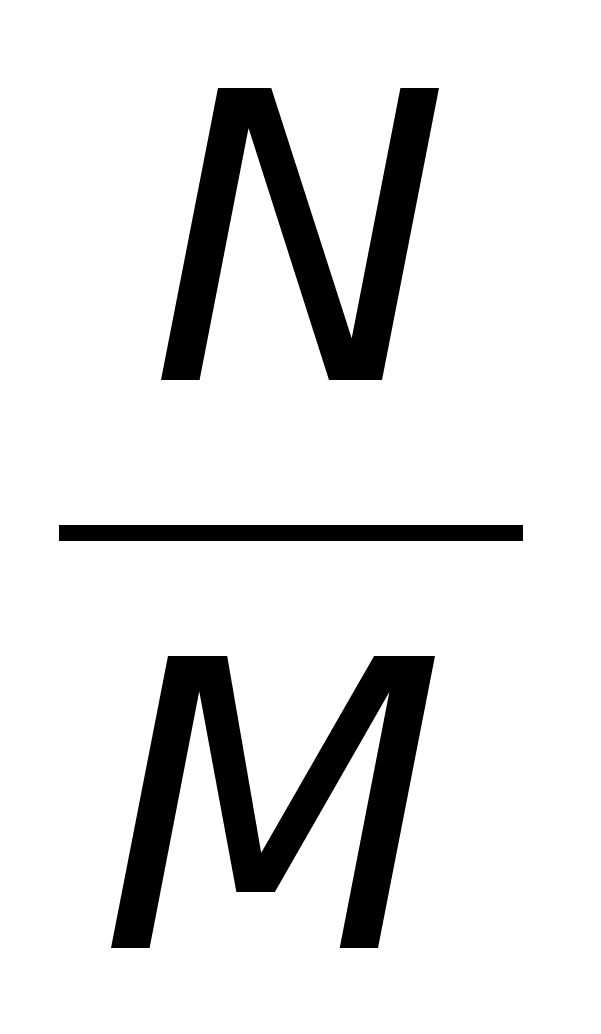
0 комментариев