Размещения данного состава

5. Размещения данного состава

Размещением данного состава  из элементов

множества  называется всякая строка длиной , составленная из элементов множества X так, что элемент  повторяется  раз, элемент  повторяется  раз , ..., элемент  повторяется  раз .

Например, если  то  есть

один из вариантов состава

Число различных размещений состава определяется по формуле:

. (1.9)

2. Бином Ньютона

Формула бинома Ньютона позволяет любой двучлен (бином) возвести в натуральную степень. Эта формула имеет вид:

 (1.10)

или сокращенно

В разложении бинома n + 1 членов. Так как , то

коэффициенты членов разложения, одинаково удаленных от начала и конца, равны между собой. При  получаем формулу для суммы биномиальных коэффициентов:

 (1.11)

Обобщением формулы бинома Ньютона является

полиномиальная формула:

 (1.12)

где  и суммирование ведется по всем наборам .

В частности:

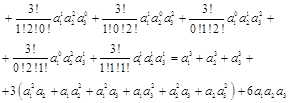
Итак,

 . (1.13)

3. Формула разложения разности n-ых степеней

 (1.14)

4. Метод математической индукции

Для вывода обобщающих формул, как правило, используют метод математической индукции.

Схема-алгоритм метода математической индукции:

1. Проверить справедливость доказываемой формулы для начального значения n (это может быть 0 , 1 , 2 , . . . ) .

2. Предположить, что формула справедлива при

3. Доказать, что формула справедлива и при

5. Формула Тейлора

Формула Тейлора позволяет данную функцию y = f (x) представить в виде многочлена со счетным числом слагаемых по степеням x:

 (1.15)

Формулы Тейлора для некоторых функций.

 

Следует помнить, что применять формулы (1.15), (1.16) или 1-6 можно для функции  только в случае, если  при .

Упражнения к § 3.1

Комбинаторика

3.1 Вычислить:

3.2 Решить уравнения и неравенства:

1) 2)

3)  4)

5)  6)  

7)  8)

3.3 Доказать:

1)  ,

2)

3)  4)

3.4 Сколько пятизначных чисел с неповторяющимися цифрами можно составить из пяти цифр:0,1,2,3,4?

3.5 Сколько различных четырехзначных чисел, делящихся на 4, можно составить из цифр1,2,3,4,5, если цифры в числе:

а) могут повторяться, б) не повторяются?

3.6 В ящике имеется 7 красных и 5 черных шаров. Сколькими способами можно выбрать из ящика 3 красных и 2 черных шара?

3.7 В вазе 10 красных и 6 белых гвоздик. Сколькими способами можно составить букет из 4-х гвоздик так, чтобы число красных гвоздик в букете было не меньше белых?

3.8 Из 10 различных цветков составляется букет, содержащий не менее трех цветков. Сколькими способами это можно сделать?

3.9 В 12-ти этажном доме на первом этаже в лифт садится 9 человек. Известно, что они выйдут группами в 2, 3 и 4 человека на разных этажах. Сколькими способами они это могут сделать, если на 2-м этаже лифт не останавливается?

Бином Ньютона

3.10 Разложить по формуле бинома Ньютона:

а)  б) , в) , г) .

3.11 Решить уравнения:

1) , 2) ,

3)  , 4)

Разложение двучлена  на множители

3.12. 1) Сократить дробь  и вычислить при х=1,

2) сократить дробь  и вычислить при a=b.

Метод математической индукции

3.13 Доказать тождества:

 

,

,

,

,

3.14 Доказать неравенства:

1)

2)

3)

4)

5)

6)

3.15 Доказать делимость:

1)  

2)

3)

3.16 Известно, что  целое число. Доказать, что

 также целое число.

3.17 Доказать, что выражение , где  простое число, делится на р (малая теорема Ферма).

Формула Тейлора

3.18 Разложить по степеням х по формуле Тейлора функции:

1) 2) .

3.19 Вычислить приближенно:

1)  с точностью 0,0001,

2)  с точностью 0,001, 3)с точностью 0,001.

§ 3.2 Комплексные числа

Введем новое недействительное число, квадрат которого равен –1. Это число обозначим символом ί и назовем мнимой единицей. Итак,

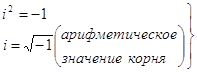 (2.1)
Тогда . (2.2)