Навигация
Действия над комплексными числами в тригонометрической и показательной формах
3. Действия над комплексными числами в тригонометрической и показательной формах
Умножение. Модуль произведения равен произведению модулей, аргумент произведения равен сумме аргументов:
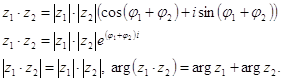 (2.16)
(2.16)
Деление. Модуль частного равен частному модулей, аргумент частного равен разности аргументов:
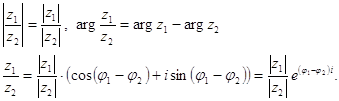 (2.17)
(2.17)
Возведение в целую степень п. Модуль возводится в степень п, аргумент умножается на п.
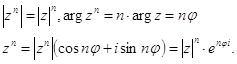 (2.18)
(2.18)
Извлечение корня степени п. Извлекается арифметический корень из модуля, общее значение аргумента делится на п. Корень имеет ровно п различных значений, если ![]()
![]() (2.19)
(2.19) ![]()
Формулы (2.18) и (2.19) называются формулами Муавра.
Упражнения к § 3.2
3.20 Выполнить действия
![]()
![]()
![]()
![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() ; 7)
; 7) ![]() ;
;
![]() 9)
9) ![]() .
.
3.21 Представить в виде суммы более простых дробей:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
3.22 Решить уравнения:
1) ![]() , 2)
, 2) ![]() , 3)
, 3) ![]() , 4)
, 4) ![]() , 5)
, 5) ![]() , 6)
, 6) ![]() , 7)
, 7) ![]() , 8)
, 8) ![]() , 9)
, 9) ![]() , 10)
, 10) ![]() , 11)
, 11) ![]() .
.
3.23 Построить на комплексной плоскости и представить в тригонометрической форме числа:
1) ![]() , 2)
, 2) ![]() , 3)
, 3) ![]() , 4)
, 4) ![]() ,
,
5) ![]() , 6)
, 6) ![]() , 7)
, 7) ![]() , 8)
, 8) ![]() ,
,
9) 5, 10) i.
3.24 Представить в показательной форме числа (указать главное значение аргумента):
![]() 2)
2) ![]() ;
;
3) ![]() 4)
4) ![]() ;
;
5) ![]() 6)
6) ![]()
7) ![]() 8)
8) ![]() 9)
9) ![]()
10) ![]()
11) ![]() 12)
12) ![]()
13) ![]() 14)
14) ![]()
3.25 Выполнить действия: 1) ![]() 2)
2)  ,
,
3) ![]() , 4)
, 4) ![]() , 5)
, 5) ![]() ,
,
6) 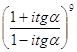 , 7)
, 7) 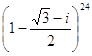 , 8)
, 8) ![]()
9) ![]() , 10)
, 10) ![]() ,
,
11) ![]() , 12)
, 12) 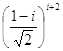 , 13)
, 13) ![]() ,
,
14) 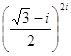 , 15)
, 15) ![]() 16)
16) ![]() 17)
17) ![]() .
.
3.26 Найти все значения корней:
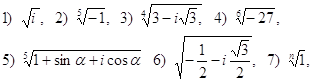
![]()
3.27. Решить уравнения:
![]()
![]()
3.28 Выразить через степени![]() и
и![]() следующие функции:
следующие функции:
![]()
3.29 Доказать:
1) 
2) 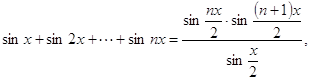
3) ![]()
![]()
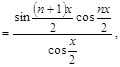 если
если ![]() .
.
Указание. Воспользуйтесь формулами Эйлера

а также формулой суммы членов геометрической прогрессии.
Глава 4 Индивидуальные домашние задания
§4.1 Индивидуальное домашнее задание (ИДЗ) по теме: “Предел функции и непрерывность”
Задача 1. Найти пределы:
Задача 2. Найти пределы.
| 2.1. | 2.2. | |||
| 2.3. | 2.4. | |||
| 2.5. | 2.6. | |||
| 2.7. | 2.8. | |||
| 2.9. | 2.10. | |||
| 2.11. |
| |||
| 2.13. | ||||
| 2.14. |
| |||
| 2.15. |
| |||
| 2.16. |
| |||
| 2.17. |
| |||
| 2.18. |
| |||
| 2.19. |
| |||
| 2.20. 2.21. | ||||
| 2.22. | ||||
| 2.23. |
| |||
| 2.25. | ||||
| 2.26. 2.27. | ||||
| 2.28. |
| |||
| 2.29. |
| |||
| 2.30. | ||||
Задача 3. Доказать непрерывность функции f(x) в точке x0.
| 3.1. f(x)=6-x2, x0=2 | 3.2. f(x)=3x2-2, x0=-2 |
| 3.3. f(x)=-2x2-3, x0=3 | 3.4. f(x)=2x2+5, x0=-3 |
| 3.5. f(x)=5x2-1, x0=4 | 3.6. f(x)=2-3x2, x0=4 |
| 3.7. f(x)=4x2-3, x0=-1 | 3.8. f(x)=4x2+5, x0=2 |
| 3.9. f(x)=x2+7, x0=-3 | 3.10. f(x)=7-2x2, x0=3 |
| 3.11. f(x)=-2x2-7, x0=2 | 3.12. f(x)=3x2+2, x0=4 |
| 3.13. f (x)=5x2+3, x0=-2 | 3.14. f(x)=4x2-1, x0=-3 |
| 3.15. f(x)=7x2-1, x0=4 | 3.16. f(x)=-8x2-1, x0=1 |
| 3.17. f(x)=2x2+11, x0=5 | 3.18. f(x)=10x2-3, x0=5 |
| 3.19. f(x)=13-2x2, x0=3 | 3.20. f(x)=3-10x2, x0=4 |
| 3.21. f(x)=4x2-11, x0=-2 | 3.22. f(x)=1-5x2, x0=2 |
| 3.23. f(x)=3-4x2, x0=1 | 3.24. f(x)=-7-x2, x0=1 |
| 3.25. f(x)=x2-6, x0=3 | 3.26. f(x)=9-5x2, x0=-2 |
| 3.27. f(x)=7-5x2, x0=-2 | 3.28. f(x)=-2x2-1, x0=3 |
| 3.29. f(x)=11-3x2, x0=2 | 3.30. f(x)=4x2-15, x0=-1 |
Задача 4. Найти пределы разложением на множители и по правилу Лопиталя.
| 4.1. | 4.2. |
| 4.3. | 4.4. |
| 4.5. | 4.6. |
| 4.7. | 4.8. |
| 4.9. | 4.10. |
| 4.11. | 4.12. |
| 4.13. | 4.14. |
| 4.15. | 4.16. |
| 4.17. | 4.18. |
| 4.19. | 4.20. |
| 4.21. | 4.22. |
| 4.23. | 4.24. |
| 4.25. | 4.26. |
| 4.27. | 4.28. |
| 4.29. | 4.30. |
Задача 5. Найти пределы, используя метод освобождения от иррациональности.
| 5.1. | 5.2. | |
| 5.3. | 5.4. | |
| 5.5. | 5.6. | |
| 5.7. | 5.8. | |
| 5.9. | 5.10. | |
| 5.11. | 5.12. | |
| 5.13. | 5.14. | |
| 5.15. | 5.16. | |
| 5.17. | 5.18. | |
| 5.19. | 5.20. | |
| 5.21. |
| |
| 5.22. | 5.23. | |
| 5.24. | 5.25. | |
| 5.26. | 5.27. | |
| 5.28. | 5.29. | |
| 5.30. | ||
Задача 6. Найти пределы, используя эквивалентные бесконечно-малые.
| 6.1. | 6.2. |
| 6.3. | 6.4. |
| 6.5. | 6.6. |
| 6.7. | 6.8. |
| 6.9. | 6.10. |
| 6.11. | 6.12. |
| 6.13. | 6.14. |
| 6.15. | 6.16. |
| 6.17. | 6.18. |
| 6.19. | 6.20. |
| 6.21. | 6.22. |
| 6.23. | 6.24. |
| 6.25. | 6.26. |
| 6.27. | 6.28. |
| 6.29. | 6.30. |
Задача 7. Найти пределы, используя эквивалентные бесконечно малые.
| 7.1. | 7.2. |
| 7.3. | 7.4. |
| 7.5. | 7.6. |
| 7.7. | 7.8. |
| 7.9. | 7.10. |
| 7.11. | 7.12. |
| 7.13. | 7.14. |
| 7.15. | 7.16. |
| 7.17. | 7.18. |
| 7.19. | 7.20. |
| 7.21. | 7.22. |
| 7.23. | 7.24. |
| 7.25. | 7.26. |
| 7.27. | 7.28. |
| 7.29. | 7.30. |
Задача 8. Найти пределы, используя эквивалентные бесконечно малые.
| 8.1. | 8.2. |
| 8.3. | 8.4. |
| 8.5. | 8.6. |
| 8.7. | 8.8. |
| 8.9. | 8.10. |
| 8.11. | 8.12. |
| 8.13. | 8.14. |
| 8.15. | 8.16. |
| 8.17. | 8.18. |
| 8.19. | 8.20. |
| 8.21. | 8.22. |
| 8.23. | 8.24. |
| 8.25. | 8.26. |
| 8.27. | 8.28. |
| 8.29. | 8.30. |
Задача 9. Используя формулы второго замечательного предела и его следствий, найти пределы функций.
| 9.1. | 9.2. |
| 9.3. | 9.4. |
| 9.5. | 9.6. |
| 9.7. | 9.8. |
| 9.9. | 9.10. |
| 9.11 | 9.12. |
| 9.13. | 9.14. |
| 9.15. | 9.16. |
| 9.17. | 9.18. |
| 9.19. | 9.20. |
| 9.21. | 9.22. |
| 9.23. | 9.24. |
| 9.25. | 9.26. |
| 9.27. | 9.28. |
| 9.29. | 9.30. |
Задача 10. Используя правило Лопиталя и эквивалентность, найти следующие пределы.
| 10.1. a) | б) |
| 10.2. а) | б) |
| 10.3. а) | б) |
| 10.4. а) | б) |
| 10.5. а) | б) |
| 10.6. а) | б) |
| 10.7. а) | б) |
| 10.8. а) | б) |
| 10.9. а) | б) |
| 10.10. а) | б) |
| 10.11. а) | б) |
| 10.12. а) | б) |
| 10.13. | б) |
| 10.14. | б) |
| 10.15. а) | б) |
| 10.16. а) | б) |
| 10.17. а) | б) |
| 10.18. а) | б) |
| 10.19. а) | б) |
| 10.20. а) | б) |
| 10.21. а) | б) |
| 10.22. а) | б) |
| 10.23. а) | б) |
| 10.24. а) | б) |
| 10.25. а) | б) |
| 10.26. а) | б) |
| 10.27. а) | б) |
| 10.28. а) | б) |
| 10.29. | б) |
| 10.30. | б) |
Задача 11. Применяя формулу Тейлора, вычислить пределы.
| 11.1 | 11.2. | |
| 11.3. | 11.4. | |
| 11.5. | 11.6. | |
| 11.7. | 11.8. | |
| 11.9. | 11.10. | |
| 11.11. | 11.12. | |
| 11.13. | 11.14. | |
| 11.15. | 11.16. | |
| 11.17. | 11.18. | |
| 11.19. | 11.20 | |
| 11.21. | 11.22. | |
| 11.23. | 11.24. | |
| 11.25. | 11.26. | |
| 11.27.
| 11.28. | |
| 11.29. | 11.30. | |
Задача 12. Найти точки разрыва, уравнения асимптот и построить схематично график функции.
| 12.1. а) | б) |
| |
| 12.2. а) | б) |
| |
| 12.3. а) | б) |
| |
| 12.4. а) | б) |
| |
| 12.5. а) | б) |
| |
| 12.6. а) | б) |
| |
| 12.7. а) | б) |
| |
| 12.8. а) | б) | ||
| 12.9. а) | б) | ||
| 12.10. а) | б) | ||
| 12.11. а) | б) | ||
| 12.12. а) | б) | ||
| 12.13. а) | б) | ||
| 12.14. а) | б) | ||
| 12.15. а) | б) | ||
| 12.16. а) | б) | ||
| 12.17. а) | б) | ||
| 12.18. а) | б) | ||
| 12.19. а) | б) | ||
| 12.20 .а) | б) | ||
| 12.21. а) | б) | ||
| 12.22. а) | б) | ||
| 12.23. а) | б) | ||
| 12.24. а) | б) | ||
| 12.25. а) | б) | ||
| 12.26. а) | б) | ||
| 12.27. а) | б) | ||
| 12.28. а) | б) | ||
| 12.29. а) | б) | ||
| 12.30. а) | б) | ||
§ 4.2 Индивидуальное домашнее задание по теме: «Производная и ее применение»
Задача 1. Найти первую производную функции:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Задача 2. Найти первую производную функции:
2.1. ![]() 2.2.
2.2. ![]()
2.3. 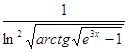 2.4.
2.4. 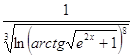
2.5. ![]() 2.6.
2.6. ![]()
2.7. ![]() 2.8
2.8 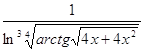
2.9. 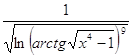 2.10.
2.10. ![]()
2.11. ![]() 2.12.
2.12. 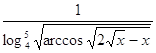
2.13. ![]() 2.14.
2.14. 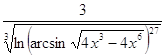
2.15. ![]() 2.16.
2.16. 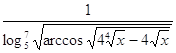
2.17. ![]() 2.18.
2.18. ![]()
2.19. 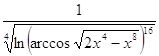
2.20. ![]()
2.21. 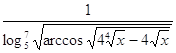
2.22. ![]()
2.23. ![]()
2.24. 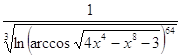
2.25. ![]()
2.26. 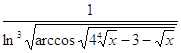
2.27. ![]()
2.28. ![]()
2.29. 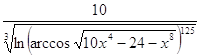
2.30. ![]()
Задача 3. Найти первую производную функции:
3.1. ![]() 3.2.
3.2. ![]()
3.3. ![]() 3.4.
3.4. ![]()
3.5. ![]() 3.6.
3.6. ![]()
3.7. ![]() 3.8.
3.8. ![]()
3.9. ![]() 3.10.
3.10. ![]() 3.11.
3.11. ![]() 3.12.
3.12. ![]()
3.13. ![]() 3.14.
3.14. ![]()
3.15. ![]() 3.16.
3.16. ![]()
3.17. ![]() 3.18.
3.18. ![]()
3.19. ![]() 3.20.
3.20. ![]()
3.21. ![]() 3.22.
3.22. ![]()
3.23. ![]() 3.24.
3.24. ![]()
3.25. ![]() 3.26.
3.26. ![]()
3.27. ![]() 3.28.
3.28. ![]()
3.29. ![]() 3.30.
3.30. ![]()
Задача 4. Найти первую производную функции:
4.1. ![]() 4.2.
4.2. ![]()
4.3. ![]() 4.4.
4.4. ![]()
4.5. ![]() 4.6.
4.6. ![]()
4.7. 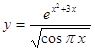 4.8.
4.8. ![]()
4.9. 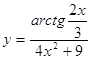 4.10.
4.10. 
4.11. ![]() 4.12.
4.12. ![]()
4.13. ![]() 4.14.
4.14. 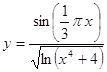
4.15. ![]() 4.16.
4.16. ![]()
4.17. 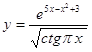 4.18.
4.18. ![]()
4.19. 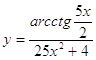 4.20.
4.20. 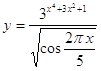
4.21. ![]() 4.22.
4.22. ![]()
4.23. ![]() 4.24.
4.24. ![]()
4.25. ![]() 4.26.
4.26. ![]()
4.27. 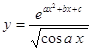 4.28.
4.28. ![]()
4.29. 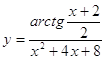 4.30.
4.30. 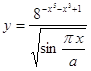
Задача 5. Найти первую производную функции:
5.1. ![]() 5.2.
5.2. ![]()
5.3 ![]() 5.4.
5.4. ![]()
5.5. ![]() 5.6.
5.6. ![]()
5.7. ![]() 5.8.
5.8. ![]()
5.9. ![]() 5.10.
5.10.![]()
5.11.![]() 5.12.
5.12. ![]()
5.13.![]() 5.14.
5.14. ![]()
5.15. ![]() 5.16.
5.16. ![]()
5.17. ![]() 5.18.
5.18. ![]()
5.19. ![]() 5.20.
5.20.![]()
5.21. ![]() 5.22.
5.22. ![]()
5.23 ![]() 5.24.
5.24. ![]()
5.25. ![]() 5.26.
5.26. ![]()
5.27. ![]() 5.28.
5.28. 
5.29. ![]() 5.30.
5.30.![]()
Задача 6. Найти первую производную функции:
6.1. 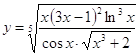 6.2.
6.2. 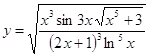
6.3. 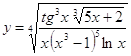 6.4.
6.4. 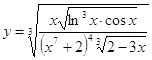
6.5. 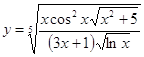 6.6.
6.6. 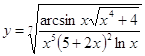
6.7. 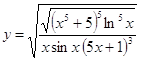 6.8.
6.8. 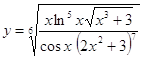
6.9. 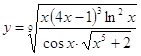 6.10.
6.10. 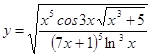
6.11. 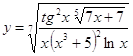 6.12.
6.12. 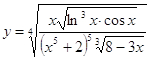
6.13. 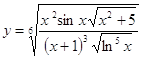 6.14.
6.14. 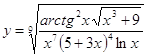
6.15. 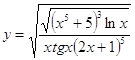 6.16.
6.16. 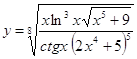
6.17. 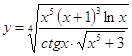 6.18.
6.18. 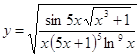
6.19. 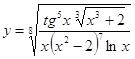 6.20.
6.20. 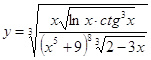
6.21. 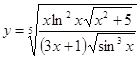 6.22.
6.22. 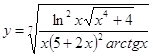
6.23. 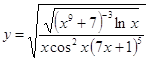 6.24.
6.24. 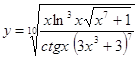
6.25. 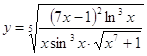 6.26.
6.26. 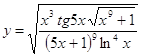
6.27. 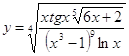 6.28.
6.28. 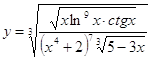
6.29. 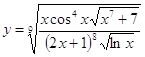 6.30.
6.30. 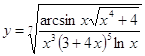
Задача 7. Найти п-ую производную функции:
7.1. ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
7.11. ![]()
7.12. ![]()
7.13. ![]()
7.14. ![]()
![]()
7.16. ![]()
7.17. ![]()
![]()
7.19. ![]()
7.20. ![]()
![]()
7.22. ![]()
![]()
7.24. ![]()
7.25. ![]()
7.26. ![]()
![]()
7.28. ![]()
7.29. ![]()
7.30. ![]()
Задача 8. С помощью формулы Лейбница найти указанную производную данной функции:
![]()
![]()
![]()
![]()
![]()
![]()
8.4. ![]()
![]()
8.5. ![]()
![]()
8.6. ![]()
![]()
8.7. ![]()
![]()
8.8. ![]()
![]()
8.9. ![]()
![]()
8.10. ![]()
![]()
8.11. ![]()
8.12. ![]()
![]()
8.13. ![]()
![]()
8.14. ![]()
![]()
8.15. ![]()
![]()
8.16. ![]()
![]()
8.17. ![]()
![]()
8.18. ![]()
![]()
8.19. ![]()
![]()
8.20. ![]()
![]()
8.21. ![]()
![]()
8.22. ![]()
![]()
8.23. ![]()
![]()
8.24. ![]()
![]()
8.25. ![]()
![]()
8.26. ![]()
![]()
8.27. ![]()
![]()
8.28. ![]()
![]()
8.29. ![]()
![]()
8.30. ![]()
![]()
Задача 9. Найти первую и вторую производные от функции у(х), заданной неявно:
9.1. ![]() 9.2.
9.2. ![]()
9.3. ![]() 9.4.
9.4. ![]()
9.5. ![]() 9.6.
9.6. ![]()
9.7. ![]() 9.8.
9.8. ![]()
9.9. ![]() 9.10.
9.10. ![]()
9.11. ![]() 9.12.
9.12. ![]()
9.13. ![]() 9.14.
9.14. ![]()
9.15. ![]() 9.16.
9.16. ![]()
9.17. ![]() 9.18.
9.18. ![]()
9.19. ![]() 9.20.
9.20. ![]()
9.21. ![]() 9.22.
9.22. ![]()
9.23. ![]() 9.24.
9.24. ![]()
9.25. ![]() 9.26.
9.26. ![]()
9.27. ![]() 9.28.
9.28. ![]()
9.29. ![]() 9.30.
9.30. ![]()
Задача 10. Найти первую и вторую производные от функции у(х), заданной параметрически:
10.1.  10.2.
10.2. 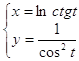
10.3. 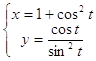 10.4.
10.4. 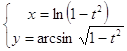
10.5. 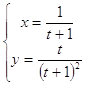 10.6.
10.6. ![]()
10.7. 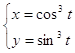 10.8.
10.8. 
10.9. 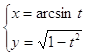 10.10.
10.10. 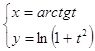
10.11. ![]() 10.12.
10.12. ![]()
10.13. 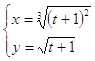 10.14.
10.14. 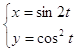
10.15. ![]() 10.16.
10.16. 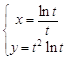
10.17. 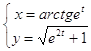 10.18.
10.18. 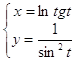
10.19. 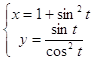 10.20.
10.20. 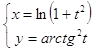
10.21. 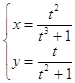 10.22.
10.22. 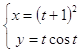
10.23. 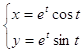 10.24.
10.24. 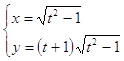
10.25. 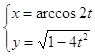 10.26.
10.26. 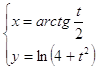
10.27. ![]() 10.28.
10.28. 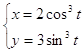
10.29. 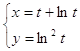 10.30.
10.30. ![]()
Задача 11. Используя геометрический смысл производной, решить следующую задачу:
11.1 Доказать, что длина отрезка, отсекаемого на оси ординат касательной в любой точке кривой у=4х – х2, равна квадрату абсциссы точки касания.
11.2 Доказать, что длина отрезка, отсекаемого на оси ординат нормалью, проведенной в любой точке кривой у=1 – х2/4, равна расстоянию от точки касания до начала координат.
11.3 Через произвольную точку кривой ху = 4 проведена касательная. Доказать, что отрезок касательной, заключенный между осями координат, делится пополам в точке касания.
11.4 Через произвольную точку кривой ху = х+2 проведена касательная. Доказать, что касательная пересекает прямую у = 1 в точке с абсциссой, равной удвоенной абсциссе точки касания.
11.5 Доказать, что площадь треугольника, образованного касательной к кривой у = 2/(1 – х),ординатой точки касания и осью абсцисс равна 1.
11.6 Доказать, что длина отрезка, отсекаемого на оси ординат касательной в любой точке кривой у=3хlnx+5x, равна утроенной абсциссе точки касания.
11.7 Через произвольную точку кривой у = а х3 проведена касательная. Доказать, что абсцисса точки пересечения касательной с осью абсцисс равна 2/3 абсциссы точки касания.
11.8 Через произвольную точку кривой у=х2 + 2/х проведена касательная. Доказать, что площадь трапеции, ограниченной осями координат, касательной и перпендикуляром, опущенным из точки касания на ось абсцисс, равна 3.
11.9 Доказать, что длина отрезка, отсекаемого на оси ординат касательной в любой точке кривой у=5х –2 х2, равна удвоенному квадрату абсциссы точки касания.
11.10 Доказать, что длина отрезка, отсекаемого на оси ординат нормалью, проведенной в любой точке кривой у= х2/2 – 1/2, равна расстоянию от точки касания до начала координат.
11.11 Через произвольную точку кривой ху =
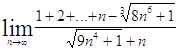
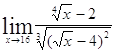
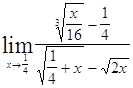
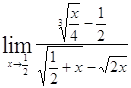
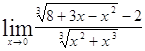
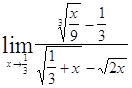
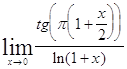
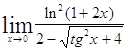
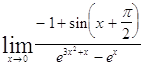
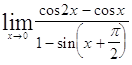
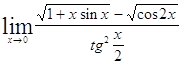
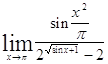
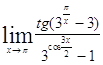
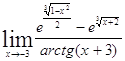
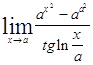
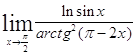
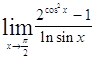
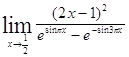
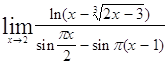
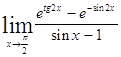
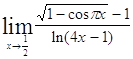
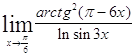
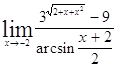
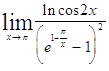
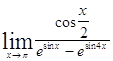
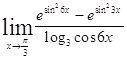
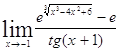
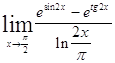
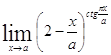
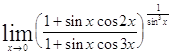
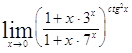
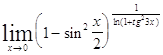
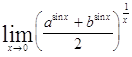
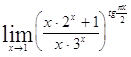

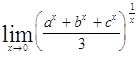
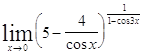
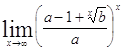 (a, b>0)
(a, b>0)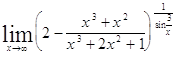
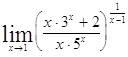

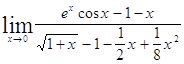
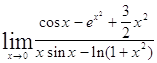
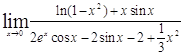
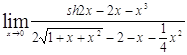


0 комментариев