Алгебраическая форма комплексного числа

1. Алгебраическая форма комплексного числа

Если , то число  (2.3)

называется комплексным числом, заданным в алгебраической форме. Это число имеет действительную часть

и мнимую часть  Так что ;

 - число, сопряженное .

Действия сложения, вычитания, умножения и возведения в степень комплексных чисел, заданных в алгебраической форме, выполняются как над многочленами.

Произведение двух сопряженных чисел есть действительное число

 (2.4)

Следовательно, сумму квадратов двух действительных чисел можно разложить на комплексные множители

 (2.5)

Деление чисел выполняется по формуле

 (2.6)

Условия равенства двух комплексных чисел

 (2.7)

2. Геометрическое представление, тригонометрическая и показательная формы комплексного числа

Прямоугольную систему координат можно использовать для геометрического представления комплексного числа.

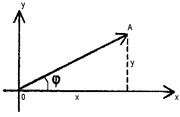Каждому комплексному числу можно поставить в соответствие точку или вектор  (рис.1).

В этом случае плоскость х0у называется комплексной плоскостью ( z ), ось 0х называется действительной осью, ось 0у называется мнимой осью. Расстояние ОА или длина вектора  называется модулем комплексного числа  Угол 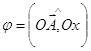 называется аргументом комплексного числа  Очевидно, каждому комплексному числу соответствует бесконечное множество аргументов.

Главное значение аргумента

Общее значение аргумента

Так как  и ,

то  (2.9)

Это тригонометрическая форма комплексного числа. Чтобы комплексное число, заданное в алгебраической форме (2.3), представить в тригонометрической форме (2.9), следует найти:

модуль по формуле  (2.10)

аргумент  по формулам :

если  1-ой четверти, то ;

если  2-ой четверти, то ;

если  3-ой четверти, то ; (2.11)

если  4-ой четверти, то ,

где вспомогательный острый угол

определяют по формуле

Если  то .

Если  то . ( 2.12)

Если  то .

Если  то .

С помощью формулы Эйлера , (2.13)

можно комплексное число представить в показательной форме

 (2.14)

Если в формуле (2.13) заменить  на -, то получим

 (2.13')

Из (2.13) и (2.13') следуют следующие формулы Эйлера:

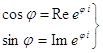
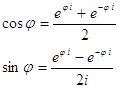  (2.15)