Формула полной вероятности

4.1 Формула полной вероятности

Группа гипотез – полная группа несовместных событий (пусть это будет Н₁, Н₂ , …, Н_n). Пусть событие А может наступить лишь при появлении одного из них. Тогда вероятность события А вычисляется по формуле:

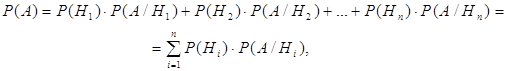 (4.1)

которая называется формулой полной вероятности.

Здесь: - вероятности гипотез;

 -условные вероятности события А.

Задачи

Задача №47. В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнения квалификационной нормы равна: для лыжников – 0,9, для велосипедистов – 0,8, для бегунов – 0,75.

Найти вероятность того, что спортсмен, вызванный наудачу, выполнит норму.

Решение.

А = {спортсмен выполнил норму};

Н₁ = {выполнил лыжник};

Н₂ = {выполнил велосипедист};

Н₃ = {выполнил бегун}.

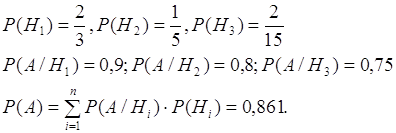
Задача №48. Стрельба производилась по 3-м мишеням. По 1-ой – 5 раз, по 2-ой – 3 раза, по 3-ей – 2 раза. Вероятность попадания по 1-ой мишени равна 0,4, по 2-ой мишени – 0,1, по 3-ей – 0,12. Найти вероятность одного попадания в мишень.

Решение. Пусть A = {попадание в мишень при одном выстреле}

H₁ = {стреляли в 1-ю мишень} P(H₁) = 0,5

H₂ = {стреляли в 2-ю мишень} P(H₂) = 0,3

H₃ = {стреляли в 3-ю мишень} P(H₃) = 0,2

P(A/H₁) = 0,4 P(A/H₂) = 0,1P(A/H₃) = 0,12

По формуле (4.1) имеем: .

Задача №49. В лаборатории 3 одинаковых клетки. В 1-й - 3 белых и 7 коричневых мыши, во 2-й – 5 белых и 6 коричневых. В 3-й – 7 белых и 2 коричневых. Случайным образом берут из одной клетки мышь. Найти вероятность того, что выбрана белая мышь (событие А).

Решение. Пусть имеется 3 гипотезы:

Н₁ = {выбрана мышь из 1-й клетки};

Н₂ = {выбрана мышь из 2-й клетки};

Н₃ = {выбрана мышь из 3-й клетки};

Р(Н₁)= Р(Н₂)= Р(Н₃)=1/3

Условные вероятности события А будут равны:

Р(А/Н₁)= 3/10; Р(А/Н₂)=5/11; Р(А/Н₃)=7/9.

По формуле (4.1) имеем:

 

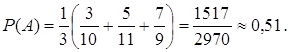
Задача №50. Судостроительный завод получает от 3-х предприятий детали: от предприятия В – 60%, от С – 30%, от D – 10%. При этом на каждом из этих предприятий допускается брак, соответственно на В – 4%, на С – 5%, и на D – 6%. Какова вероятность того, что случайно выбранная деталь будет бракованной (событие А), если известно, от какого предприятия она поступила.

Решение. В качестве гипотез событий примем:

Н₁ = {деталь поступила от предприятия В};

Н₂ = {деталь поступила от предприятия С};

Н₃ = {деталь поступила от предприятия D}.

Р(Н₁) = 0,6; Р(Н₂) = 0,3; Р(Н₃) = 0,1

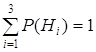
Условные вероятности события А равны соответственно:

Р(А/Н₁)= 0,04;Р(А/Н₂)=0,05;Р(А/Н₃)=0,06.

По формуле (4.1) имеем:

Задача №51. В магазин поступили телевизоры от 5-ти фирм в следующем количестве:

Фирма	1	2	3	4	5
Количество телевизоров	5	10	6	8	11
Рi	0,98	0,8	0,6	0,3	0,1

Р_i – вероятности того, что телевизоры исправны.

Найти вероятности того, что купленный наугад телевизор исправно работает (событие А)

Решение.

1) В качестве гипотез выберем события:

{телевизор i-й фирмы}, (i=).

2) Найдём вероятности гипотез, учитывая, что п=40:

Р(Н₁) = 5/40; Р(Н₂) = 10/40; Р(Н₃) = 6/40; Р(Н₄) = 8/40; Р(Н₅) = 11/40.

3) Условные вероятности равны:

Р(А/Н₁) = 0,98; Р(А/Н₂) = 0,8; Р(А/Н₃) = 0,6; Р(А/Н₄) = 0,3; Р(А/Н₅) = 0,1.

4) По формуле (4.1) имеем:

Задача №52. Имеются 3 одинаковых ящика, в каждом из которых по 20 однотипных деталей. Определить вероятность того, что извлечённая из наугад выбранного ящика деталь стандартная (событие А), если известно, что в 1-м ящике 18 стандартных деталей, во 2-м – 17, в 3-м – 16.

Решение. Если в качестве i-й гипотезы (i = 1,2,3) выбрать событие

Н_i = {деталь из i-го ящика}, то Р(Н_i) =1/3.

Р(А/Н₁) = 18/20;

Р(А/Н₂) = 17/20;

Р(А/Н₃) = 16/20.

По формуле (4.1) имеем: