Навигация
Сбалансированные траектории
2. Сбалансированные траектории
Прежде всего, определим сбалансированные траектории. Пусть модель задана уравнением (2), и ![]() .
.
ПРЕДЛОЖЕНИЕ 1. Следующие три определения эквивалентны.
А. Траектория называется сбалансированной, если
![]() (3)
(3)
![]() (4)
(4)
Б. Траектория называется сбалансированной, если
![]()
В. Траектория называется сбалансированной, если
![]()
Равенство (3) представляет собой основную гипотезу модели Солоу (Solow, 1956). Равенство (4) – это один из пяти стилизованных фактов экономического роста, сформулированных Кальдором (Kaldor, 1961), этот факт входит в явном виде в формулировку AK-модели (Frankel, 1962). Равенство
![]()
(вместе с гипотезой о постоянном темпе роста труда) представляет еще один стилизованный факт Кальдора: душевой выпуск растет темпом, который примерно постоянен.
При доказательстве предложения 1 будет использоваться следующая лемма.
ЛЕММА 1. Если величины ![]() - ненулевые, имеют постоянные темпы, и
- ненулевые, имеют постоянные темпы, и
![]() ,
,
то их темпы роста совпадают.
ДОКАЗАТЕЛЬСТВО ЛЕММЫ. Предположим противное:
![]() ,
,
![]() .
.
Пусть, для определенности, ![]() . Тогда
. Тогда
![]() .
.
При ![]() , левая часть равенства стремится к постоянной
, левая часть равенства стремится к постоянной ![]() , тогда как модуль правой части стремится к 0 или к
, тогда как модуль правой части стремится к 0 или к ![]() . Полученное противоречие показывает, что
. Полученное противоречие показывает, что ![]() ■
■
ДОКАЗАТЕЛЬСТВО ПРЕДЛОЖЕНИЯ. А![]() Б. Из (2) следует, что
Б. Из (2) следует, что
![]()
Здесь правая часть постоянна, следовательно
![]() , тогда
, тогда ![]() (в силу (4)) и
(в силу (4)) и ![]() (в силу (3)).
(в силу (3)).
Б![]() В. Из (2) следует, что
В. Из (2) следует, что
![]() .
.
Левая часть постоянна, а слагаемые в правой части имеют постоянные темпы прироста. По лемме, темпы прироста величин
![]() равны, следовательно,
равны, следовательно,![]() Поскольку
Поскольку ![]() , из (2) вытекает, что
, из (2) вытекает, что
![]()
В этом равенстве правая и левая части имеют постоянные темпы прироста, следовательно, эти темпы совпадают:
![]()
В![]() А. Очевидно ■
А. Очевидно ■
Обозначим общий темп прироста переменных ![]() на сбалансированной траектории через
на сбалансированной траектории через ![]() . Следствием предложения 1 является следующее утверждение, которое можно рассматривать как обобщение теоремы Узавы (см. далее предложение 3). Введем обозначение
. Следствием предложения 1 является следующее утверждение, которое можно рассматривать как обобщение теоремы Узавы (см. далее предложение 3). Введем обозначение ![]() .
.
ПРЕДЛОЖЕНИЕ 2. Всякая сбалансированная траектория может быть построена при помощи двухфакторной производственной функции с трудосберегающим техническим прогрессом
![]() (5)
(5)
где G – неоклассическая функция (т.е. обладающая стандартными свойствами производственной функции, в частности, имеющая постоянную отдачу от масштаба – CRS). При этом темп прироста технического прогресса совпадает с темпом прироста душевого дохода:
![]()
ДОКАЗАТЕЛЬСТВО. Пусть ![]() – произвольная неоклассическая функция. Можно подобрать число
– произвольная неоклассическая функция. Можно подобрать число ![]() так, что
так, что
![]() .
.
Пусть ![]()
Тогда на сбалансированной траектории
![]() по свойству CRS
по свойству CRS
![]() по предложению 1
по предложению 1
![]() ■
■![]()
Таким образом, если модель задана посредством некоторой CRS производственной функции F, то на сбалансированной траектории может действовать также и другая CRS производственная функция G любого вида с трудосберегающим техническим прогрессом. Отсюда следует невозможность однозначного выбора производственной функции, если наблюдаемая траектория - сбалансированная.
Заметим, что полученное в предложении 2 представление G производственной функции не связано со структурой изначально заданной функции F. На сбалансированной траектории значения функций F и G совпадают, однако функция G не наследует никаких других свойств функции F.
Смысл предложения 2 весьма прозрачен. Как следует из предложения 1, на сбалансированной траектории капитал и выпуск растут общим темпом, а рост труда «не дотягивает» до этого темпа. Если технический прогресс придаст эффективному труду необходимую добавку темпа, то капитал и эффективный труд будут расти одним темпом, что обеспечит роста выпуска тем же темпом.
Вид (5) – не единственный вид производственной функции, который приводит к данной сбалансированной траектории. Например, ту же сбалансированную траекторию может определять функция Леонтьева или производственная функция AK-модели
![]()
где ![]()
Такого рода неоднозначность уменьшается, если ограничить множество сбалансированных траекторий условием постоянства долей факторов.
ПРЕДЛОЖЕНИЕ 3 (Теорема Узавы – см. Uzawa, 1961, Jones, Scrimgeour, 2005). Если модель определена непрерывно дифференцируемой CRS производственной функцией ![]() , и на сбалансированной траектории доли факторов
, и на сбалансированной траектории доли факторов
![]()
постоянны во времени[5], то (5) – единственно возможное представление производственной функции F на этой траектории.
Доказательство см. в Jones, Scrimgeour, 2005■
Хотя предложение 3 сужает, по сравнению с предложением 2, класс производственных функций, пригодных для построения сбалансированной траектории, оно не позволяет выявить вид функции F вне этой траектории. Т.е. невозможно однозначно специфицировать производственную функцию, наблюдая лишь одну сбалансированную траекторию.
Пусть, например,
![]() - сбалансированная траектория,
- сбалансированная траектория,
![]()
![]() - известные доли капитала и труда на этой траектории, и мы хотим специфицировать CES функцию
- известные доли капитала и труда на этой траектории, и мы хотим специфицировать CES функцию
![]()
В таком случае начальный уровень технического прогресса ![]() и параметры CES функции
и параметры CES функции ![]() удовлетворяют системе уравнений
удовлетворяют системе уравнений
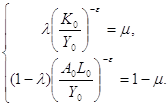
Однако, тройка ![]() определяется этой системой неоднозначно.
определяется этой системой неоднозначно.
Особенность двухфакторной функции Кобба-Дугласа в том, что для нее множитель ![]() может трактоваться не только как трудосберегающий (нейтральный по Харроду) технический прогресс, но еще и как капиталосберегающий (нейтральный по Солоу) и как увеличивающий TFP (нейтральный по Хиксу) прогресс:
может трактоваться не только как трудосберегающий (нейтральный по Харроду) технический прогресс, но еще и как капиталосберегающий (нейтральный по Солоу) и как увеличивающий TFP (нейтральный по Хиксу) прогресс:
![]()
![]()
![]()
![]()
![]() .
.
Поэтому теорему Узавы формулируют еще так: если на сбалансированной траектории доли факторов постоянны, то либо имеет место трудосберегающий технический прогресс, либо действует производственная функция Кобба-Дугласа.
Применительно к трехфакторной функции с природными ресурсами предложение 2 может быть переформулировано следующим образом.
ПРЕДЛОЖЕНИЕ 4. Пусть сбалансированная траектория такова, что ![]() . Тогда эта траектория может быть построена при помощи трехфакторной производственной функции с трудосберегающим и ресурсосберегающим техническим прогрессом
. Тогда эта траектория может быть построена при помощи трехфакторной производственной функции с трудосберегающим и ресурсосберегающим техническим прогрессом
![]() , (6)
, (6)
где ![]() , G – неоклассическая функция.
, G – неоклассическая функция.
ДОКАЗАТЕЛЬСТВО. Аналогично доказательству предложения 2, для произвольной CRS функции G подберем числа ![]() так, что
так, что
![]() .
.
Определим функции
![]()
Тогда на сбалансированной траектории
![]() по свойству постоянной отдачи от масштаба
по свойству постоянной отдачи от масштаба
![]() по предложению 1
по предложению 1
![]() ■
■
Обобщением теоремы Узавы для случая трехфакторной модели является следующее утверждение.
ПРЕДЛОЖЕНИЕ 5. Если модель определена непрерывно дифференцируемой CRS производственной функцией
![]()
и на сбалансированной траектории доли факторов
![]()
постоянны во времени, то (6) – единственно возможное представление производственной функции на этой траектории.
ДОКАЗАТЕЛЬСТВО. Введем обозначения
![]()
Заметим, что при экзогенно заданных
![]()
траектория
![]()
определена последовательностью ![]() (восстанавливается по этой последовательности), таким образом можно представить траекторию как
(восстанавливается по этой последовательности), таким образом можно представить траекторию как
![]() .
.
На произвольной траектории в момент t, эластичность y по x равна отношению доли капитала ![]() к суммарной доли остальных двух факторов:
к суммарной доли остальных двух факторов:
![]() . (7)
. (7)
Действительно,
![]()
следовательно
![]() ,
,
отсюда
![]() ,
,
т.е.
![]() ,
,
откуда следует (7).
В силу предложения 1, на сбалансированной траектории величина
![]() сохраняется
сохраняется
На сбалансированной траектории с постоянными долями факторов имеет место равенство
![]() .
.
Решая это дифференциальное уравнение, получаем
![]() ,
,
где ![]() - некоторые функции. Отсюда, аналогично тому, как это сделано в Jones, Scrimgeour, 2005 для двухфакторной производственной функции, можно получить, что
- некоторые функции. Отсюда, аналогично тому, как это сделано в Jones, Scrimgeour, 2005 для двухфакторной производственной функции, можно получить, что
![]() .
.
Поскольку труд ![]() и используемые природные ресурсы
и используемые природные ресурсы ![]() входят в формулировку модели симметрично, функция
входят в формулировку модели симметрично, функция ![]() также сепарабельна, т.е.
также сепарабельна, т.е.
![]() ■
■
Для функции Кобба-Дугласа
![]()
технический прогресс можно трактовать как трудо- и ресурсосберегающий одновременно, но еще и как только трудосберегающий, только ресурсосберегающий, а также как капиталосберегающий или как увеличивающий TFP.
Функция CES
![]()
обладает тем достоинством, что доли факторов на сбалансированной траектории постоянны, если прогресс является трудосберегающим и ресурсосберегающим. Действительно, пусть
![]() ,
, ![]()
Тогда доля труда на сбалансированной траектории равна
![]()
Аналогично проверяется постоянство доли природных ресурсов на сбалансированной траектории.
Похожие работы
... прибылях и убытках, отчет об уровне достаточности капитала, величина резервов на покрытие сомнительных ссуд и иных активов. Оценка же экономического положения производится ежеквартально. В ходе оценки финансово-хозяйственной деятельности коммерческих кредитных организаций анализируются: -показатели оценки капитала; -показатели оценки активов; -показатели оценки доходности; -показатели оценки ...
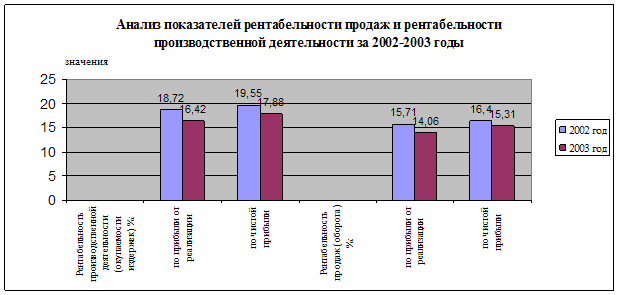
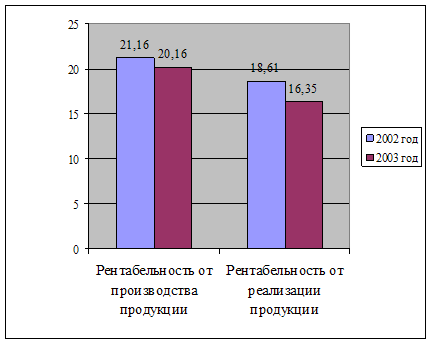
... группы. Факторы повышения рентабельности зависят от единых экономических явлений и процессов. 2. Анализ рентабельности объема производства ЧУП «Цветлит» 2.1 Экономико-организационная характеристика объекта исследования Объектом исследования является частное унитарное предприятие «Цветлит». Полное наименование предприятия – Гродненское учебно-производственное унитарное предприятие «Цветлит ...
... бы хорошим ни было местное правительство, бедному штату потребуется помощь со стороны федерального правительства, чтобы стимулировать развитие. Современные политики Бразилии руководствуются идеей о том, что современная региональная политика предусматривает инвестиции в население бедных регионов (здравоохранение и образование), увеличение объема инвестиций в инфраструктуру, а также предоставление ...
... , регионального и муниципального уровней на всех субъектов региональной инвестиционной системы в интересах достижения намеченных целей инвестиционного развития региона. 3. Перспективы стимулирования и активизации инвестиционной деятельности в России Потребность страны в иностранных инвестициях составляет 10-12 млрд. долларов в год. Для стабилизации экономики и активизации инвестиционного ...

0 комментариев