Абсолютные разности

13. Абсолютные разности

Индексный анализ независимо от метода построения цепи взаимосвязанных индексов дополняется анализом абсолютных разностей.

Абсолютная разность – это разность между числителем и знаменателем индекса (общего или агрегатного). Точно так же, как существует балансовая связь между общим и агрегатными индексами, существует такая же связь и между абсолютными разностями.

Абсолютная разность по общему индексу равна сумме абсолютных разностей по агрегатным индексам. В общем виде в обозначениях рассмотренного выше примера (А = CmFl) это записывается так:

.

Это уравнение указывает на основное назначение данного анализа; именно наличие баланса абсолютных разностей убеждает в правильности выполненных расчетов. Кроме того, абсолютные разности более точно учитывают дисбаланс. В связи с этим абсолютные разности по разным общим признакам имеют разные пределы дисбаланса.

Абсолютные разности очень существенно дополняют индексный анализ по другой причине. Дело в том, что если индексный анализ всегда замкнут совокупностью (генеральной ее частью), то абсолютная разность может применяться для любых частей совокупности, даже для отдельных единиц совокупности (характерных представителей). Докажем это утверждение. Пусть формула общего индекса имеет вид

.

Если замкнуть рамки индексного анализа представителями совокупности, общий индекс преобразуется к виду

.

Это выражение непосредственно трансформируется в произведение двух индивидуальных индексов: .

Вместе с тем для отдельной единицы совокупности абсолютная разность по общему признаку может быть рассчитана, поскольку . Аналогично получим абсолютные разности вследствие изменения количественного и качественного признаков соответственно:

;

.

Абсолютные разности в отличие от индексов – числа именованные, и потому они более наглядны, а в стоимостном измерении сопоставимы.

Следует помнить, что абсолютные разности классической природы всегда гарантируют баланс независимо от того, замыкается ли анализ рамками совокупности (генеральной части) или отдельными ее представителями. При этом абсолютные разности не образуются на базе модификаций классических индексов.

Метод цепных подстановок. Пусть исходный признак Z рассчитывается по формуле Z = aBC. После ранжирования факторов (Z = BCa) запишем общий индекс, агрегатные индексы и соответствующие абсолютные разности:

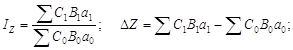
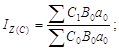
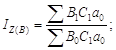
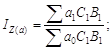
Абсолютные разности для характерного представителя совокупности следующие:

Полная идентичность записи и последовательности процедур анализа позволяет итоговый и промежуточные результаты для отдельных единиц совокупности сопоставлять с такими же результатами по совокупности в целом. Кроме того, результаты абсолютных разностей можно представить в относительном измерении:

и т.д. В таком варианте результаты могут быть отнесены к индексной базе, что позволяет получить целый набор индексов: для единиц совокупности – индивидуальные и групповые, а для совокупности в целом – агрегатные частные и модифицированные индексы.

Система модифицированных агрегатных индексов используется в статистике для корректировки средних, для уточнения показателей вариации и для разработки шести статистических моментов.

Метод индивидуального учета факторов. Выполним аналогичную процедуру формирования абсолютных разностей. Запишем общий и агрегатные индексы:

.

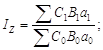
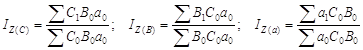Абсолютные разности для совокупности

.

Абсолютные разности для отдельного представителя совокупности

Общие выводы о целесообразности расчета абсолютных разностей справедливы и в этом случае. Однако этот метод менее надежен, чем предыдущий, что сказывается и на результатах анализа через абсолютные разности. Проявляется это в нарушении баланса уже при четырех признаках. Допустимые пределы дисбаланса для количественных признаков с устойчивым модулем качества 2-4 %, с неустойчивым 3-5 %.

14. Общие индексы качественных признаков – индексы средних

Эта группа индексов представляет собой подсистему общих индексов качества и агрегатных индексов, сформированных на их основе. Построение общих индексов такого типа имеет ряд особенностей:

1. Поскольку изучаемым общим признаком является качественный, то сопоставляются его средние уровни в пределах совокупности (генеральной ее части).

2. Любой общий индекс качества можно представить как комбинацию общего индекса количества и индивидуального индекса количества.

3. Система агрегатных индексов, построенных на основе общего индекса качества, содержит только два индекса: индекс фиксированного состава и индекс структурных сдвигов.

4. Комплексный индексный анализ обязательно дополняется анализом абсолютных разностей, которые регистрируют изменение количественного признака, основным элементом которого является изучаемый качественный признак.

5. Для тех качественных признаков, которые имеют обратную связь (производительность и трудоемкость, фондоемкость и фондоотдача) составляются два варианта общих индексов качества: прямой и обратный.

Из общей теории статистики известно, что качественные признаки – мера качества, которая может быть индивидуальной (для каждой единицы совокупности) или общей (средний уровень по изучаемой совокупности). Поэтому формирование общего индекса качественного признака предполагает соизмерение среднего его значения по совокупности или генеральной части соответственно в отчетном и базисном периоде.

Рассмотрим специфику формирования таких индексов на примере показателя себестоимости. Общая формула для индекса себестоимости имеет вид

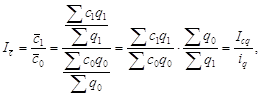
где с₁ и с₀ – показатели себестоимости по единицам совокупности соответственно в отчетном и базисном периодах; q₁ и q₀ – объем выпуска продукции по единицам совокупности в отчетном и базисном периодах;  и  – средняя себестоимость по совокупности в отчетном и базисном периодах.

Полученное выражение не является стадией комплексного статистического анализа, а используется для определения группового и общего индексов количества.

Вернемся к развернутой записи общего индекса: первый сомножитель в ней – общий индекс количества

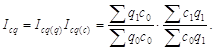
Поменяв индексы местами и разделив второй на дробь  получим

.

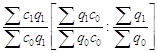Выполнив сначала действия в скобках, после преобразований получим произведение агрегатных индексов общего индекса себестоимости:

.

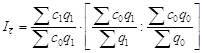Общий индекс в такой записи получил название индекса переменного состава. Первый из агрегатных индексов – индекс фиксированного состава; второй – индекс структурных сдвигов.

Индекс фиксированного состава регистрирует изменение себестоимости (общего признака) за счет колебаний себестоимости по единицам совокупности. Эти изменения фиксируются при неизменной структуре совокупности. Последняя оценивается через признак, жестко связанный с изучаемым, – объем производства. При этом относительные величины структуры формируются, исходя из фактических значений такого признака.

Индекс структурных сдвигов, несмотря на необычность его записи, не нарушает записи общего индекса: делимое (числитель) – средняя себестоимость базисного периода при фактической структуре выпуска продукции; делитель (знаменатель) – та же средняя, но при базовой структуре выпуска продукции. Таким образом, этот индекс регистрирует изменение себестоимости вследствие изменений в структуре производства.

Кроме содержательных различий агрегатных индексов, различны и их функции: индекс фиксированного состава регистрирует изменение себестоимости под влиянием внутренних факторов, индекс структурных сдвигов – под влиянием внешних факторов.

В конкретной практике классическая форма индекса фиксированного состава не всегда возможна (например, при расчете индекса цен). В таких случаях используют специальные приемы формирования таких индексов, в основе которых лежит модуль индекса Струмилина.

Абсолютные разности. Абсолютные разности всегда определяются только по количественным признакам. Это требование статистики является исходным для анализа абсолютных разностей любой системы взаимосвязанных индексов. В рассматриваемом случае количественным признаком однородного содержания с изучаемым является сумма производственных затрат (издержки производства). Обозначим ее С. Тогда

С = с_iq_i,

где с_i – cебестоимость продукции у единицы совокупности; q_i – объем продукции у каждой из единиц изучаемой совокупности.

Абсолютная разность сложного количественного признака (в данном случае производственных затрат) определяется как разность числителя и знаменателя его общего индекса:

где DС – абсолютная разность производственных затрат; с₁ и с₀ – индивидуальные значения себестоимости у единиц изучаемой совокупности в отчетном и базисном периодах соответственно; q₁ и q₀ – объемы производства по единицам совокупности в отчетном и базисном периодах соответственно.

Если вместо индивидуальных значений себестоимости использовать среднюю себестоимость  то формула для расчета производственных затрат примет вид

Следовательно, изменение производственных затрат можно рассматривать в зависимости от колебаний фактических значений средней от плановых себестоимости и объемов производства в целом по изучаемой совокупности. Иначе говоря, абсолютная разность производственных затрат может быть представлена как сумма

где ΔС_Sq и  – абсолютные разности производственных затрат вследствие изменений объема производства и средней себестоимости соответственно.

В свою очередь, первое слагаемое, которое регистрирует изменение производственных затрат под влиянием объема производства, в развернутом виде может быть записано следующим образом:

Второе слагаемое, характеризующее изменение производственных затрат из-за колебаний средней себестоимости, может быть выражено так:

Это общая запись абсолютной разности сложного признака (производственных затрат), в состав которого входит изучаемый качественный признак (себестоимость); ее можно дифференцировать, используя формулы агрегатных индексов, выступающих как структурные элементы индекса переменного состава: индекса фиксированного состава  и индекса структурных сдвигов .

В дифференцированной записи

Запишем слагаемые в развернутом виде:

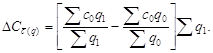
Таким образом, первое слагаемое  является разностью между числителем и знаменателем индекса фиксированного состава, а составляющая  – соответственно разностью делимого и делителя индекса структурных сдвигов, умноженной на суммарный объем производства в отчетном периоде.

Из стоимостных качественных показателей только себестоимость позволяет сформировать индекс фиксированного состава. Все остальные стоимостные показатели для выполнения индексного анализа требуют применения индексов Струмилина.

Особенности построения общих индексов качества обратным методом. Рассмотрим эти особенности на примере индекса производительности труда. Введем следующие обозначения: р – производительность труда; Q – объем производства; N – численность работников (затраты живого труда). Тогда .

Процедура построения индекса переменного состава прямым методом аналогична рассмотренной выше процедуре формирования этого индекса для себестоимости:

· сначала записываем индекс переменного состава (индекс средней производительности труда) в общем виде:

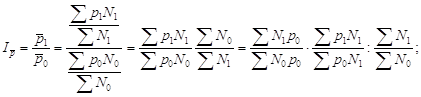
· затем путем перестановки сомножителей и делением второго на дробь  получаем развернутую запись индекса переменного состава:

,

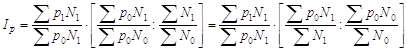где  – индекс фиксированного состава производительности труда;  – индекс структурных сдвигов этого показателя,

.

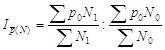Анализ с использованием индексов качества подразумевает две стадии: индексный анализ и анализ через абсолютные разности.

Порядок выполнения анализа на базе абсолютных разностей рассмотрен выше для показателя себестоимости. При первом методе определения производительности этот порядок сохраняется. Вначале выбирается сложный количественный признак, в состав которого входит изучаемый (производительность труда). Таким признаком является объем производства .

Выразим объем производства через среднюю производительность труда  и суммарные затраты живого труда (численность работников в целом по изучаемой совокупности SN).

Абсолютная разность объема производства в общем виде

где

Величина  может быть записана в более конкретном виде с учетом влияния факторов, вызывающих изменение средней производительности труда:

Первое слагаемое этой суммы определяется как разность числителя и знаменателя индекса фиксированного состава , второе – соответственно как разность делимого и делителя индекса структурных сдвигов , умноженная на суммарную численность в отчетном периоде:

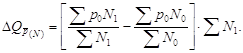
Кроме прямого способа расчета показателя производительности труда, существует обратный (через трудоемкость):  где t – трудоемкость работ. Отсюда  т.е. индивидуальный индекс производительности труда через трудоемкость является зеркальным отражением индивидуального индекса этого показателя при прямом способе его расчета . С учетом этой зависимости запись процедуры формирования общего индекса производительности труда обратным способом и выделения его составляющих (индексов фиксированного состава и структуры) выглядит следующим образом:

.

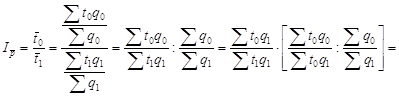
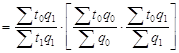Анализ записи формулы позволяет выделить два основных момента обратного порядка регистрации общего индекса качества и его составляющих:

· в обратной записи индексное число является зеркальным отражением его дроби в прямой записи (в прямой записи  в обратной

· «веса» в агрегатных индексах не меняют своих временных значений и остаются такими же, как в прямой записи.

Обратный порядок формирования общего индекса качества должен использоваться в следующих случаях:

1) при отсутствии информации (полном или частичном) для расчета изучаемого признака прямым методом;

2) в случае, когда объем продукции представлен продукцией разных наименований или услугами разного содержания. Именно это очень часто определяет выбор записи и, как следствие, необходимость переводить продукцию в трудовое измерение;

3) для универсальных вариантов анализа различных блоков промышленных групп ХС или финансово-промышленных групп.

Рекомендательный библиографический список

Основной:

1. Ефимова М.Р. Общая теория статистики: Учебник / М.Р.Ефимова, Е.В.Петрова, В.Н.Румянцев. М.: ИНФРА-М, 1998. 416 с.

2. Общая теория статистики: Учебник / И.И.Елисеева, М.М.Юзбашев. М.: Финансы и статистика, 2002. 280 с.

3. Общая теория статистики: Учебник / Под ред. Г.С.Кильдишева. М.: Статистика, 1980. 432 с.

4. Теория статистики: Учебник / Под ред. Р.А.Шмоловой. М.: Финансы и статистика, 2002. 560 с.

Дополнительный:

5. Гусаров В.М. Теория статистики: Учеб. пособие для вузов. М.: Аудит, ЮНИТИ, 1998. 247 с.

6. Дубров А.М. Многомерные статистические методы / А.М.Дубров, В.С.Мхитарян, Л.И.Трошин. М.: Финансы и статистика, 2001. 368 с.

7. Практикум по теории статистики: Учеб. пособие / Под ред. Р.А.Шмоловой. М.: Финансы и статистика, 2002. 416 с.

Оглавление

Введение

1. Статистическое наблюдение. Классификация признаков явлений

2. Сводка и группировка

3. Ряды распределения

4. Графическое изображение рядов распределения

4.1. Уровневые графики (гистограмма, полигон распределения)

4.2. Интегральные графики

5. Динамические ряды

6. Статистические таблицы

7. Абсолютные и относительные величины

8. Средние величины

8.1. Понятие о средних в статистике

8.2. Научные основы исчисления средних величин

8.3. Неформальное взвешивание при расчете статистических средних

9. Вариация признаков и статистические способы ее измерения

10. Дисперсионный анализ

11. Индексы

12. Общие индексы количественных признаков

13. Абсолютные разности

14. Общие индексы качественных признаков – индексы средних

Рекомендательный библиографический список

* В качестве оценочного критерия для россыпей принято критическое содержание, превышающее среднее в 8-13 раз.

* Для составления пропорции используем любой уровень ряда столбцов 5 и 6. Здесь использован 4-й уровень.

* Попадание медианы в нижний интервал исключено.

Похожие работы

Статистические наблюдения

Скачать

21040

0

0

... восприятии. Статистическим можно назвать лишь такое наблюдение, которое обеспечивает регистрацию устанавливаемых фактов в учетных документах для последующего их обобщения. Конкретными примерами статистического наблюдения служит систематическое собирание сведений, например на машиностроительных предприятиях о количестве произведенных машин и узлов, издержках производства, прибыли и т. д. ...

Статистическое наблюдение в коммерческом праве

Скачать

38681

0

0

... котором ответы на изучаемые вопросы записываются со слов опрашиваемого. К опросу, например, прибегают при переписи населения. Однако, опрос может быть организован по разному. В статистическом наблюдении коммерческого права принято выделять следующие его виды: Þ   Устный(экспедиционный) способ заключается в том, что специально подготовленные работники, которых обычно называют счетчиками, ...

Сущность и методы статистического наблюдения

Скачать

59505

7

7

... для малых предприятий всех организационно-правовых форм и форм собственности и годовая форма, содержащая показатели производственной деятельности этих предприятий. Общее руководство статистическим наблюдением за деятельностью коммерческих банков возложено на Банк России, который совместно с органами государственной статистики разрабатывает формы статистической отчетности и инструкции по их ...

Статистическое наблюдение, первоначальная обработка и представление ее данных

Скачать

20196

0

1

... проведения наблюдения. Статистический формуляр - это учетный документ, который включает в себя адресную характеристику объекта наблюдения и статистические данные про него. Это могут быть переписные и отчетные листы, анкеты и т.п. Организационные вопросы статистического наблюдения Второй составляющей плана наблюдения являются организационные вопросы, которые определяют: органы и персонал ( ...