Сводка и группировка
Формируется ряд (с равными интервалами) на базе ряда распределения
Интегральные графики
Динамические ряды
Средние величины
Неформальное взвешивание при расчете статистических средних
Вариация признаков и статистические способы ее измерения
Дисперсионный анализ
Характер стандартности признака
Общие индексы количественных признаков
При таком расположении признаков первый индекс будет обязательно индексом количества, а последний – индексом качества
Абсолютные разности
Навигация
Формируется ряд (с равными интервалами) на базе ряда распределения
Статистическое наблюдение
111617
знаков
3
таблицы
3
изображения
1. Формируется ряд (с равными интервалами) на базе ряда распределения.
2. Выполняется графическая проверка полученного результата. График строится следующим образом: по оси абсцисс откладывают интервалы ряда с регистрацией их средних, по оси ординат – частоты (частости). Точки графика получают на пересечении срединных значений уровней ряда и соответствующих ординат.
3. Проводится анализ полученного графика посредством построения линии тренда. Если линия тренда представляет собой прямую линию или параболическую кривую (второго порядка), то полученные результаты являются достаточно надежными (качественными) и группировку можно закончить. Если линия тренда представлена гиперболической или синусоидальной кривой, то результаты группировки нельзя признать надежными и процедуру следует продолжить. Как правило, последующие стадии группировки заканчиваются построением рядов с неравными интервалами.
4. Осуществляется процедура проверки рядов с неравными интервалами:
1) по исходным данным определяется плотность распределения признака в пределах интервала по единицам совокупности;
2) строится график, в котором по оси абсцисс откладывают интервалы ряда с регистрацией середины; по оси ординат – плотность распределения;
3) проводится анализ полученного результата.
Кроме того, результатами группировки могут быть смешанные ряды, когда одни уровни представлены интервальными значениями, а другие – дискретными (геостатистика, гидрометеорологические исследования).
4. Графическое изображение рядов распределения
Любой ряд распределения может быть представлен в виде статистического графика. При этом по оси ординат показываются частоты (частости, плотности распределения), по оси абсцисс – значения признаков.
Построение статистических графиков отличается от построения математических рядом особенностей:
1. Для большей наглядности допускаются разные масштабы по осям координат.
2. Статистические графики могут быть уровневыми и интегральными. Уровневые замыкаются числом или пределами частот, что позволяет комплектовать уровневые статистические графики взаимосвязанных показателей на одном листе.
3. Статистические графики могут строиться как в абсолютном, так и в относительном измерении (по признаку). Последние предпочтительнее для функциональных признаков.
4. Интегральные статистические графики предполагают суммирование не только значений признака, но и частот. При этом возможно полное суммирование последних или их суммирование в ограниченных пределах (интервалах).
5. Статистические графики в зависимости от цели исследований читаются слева направо (прямой порядок) и справа налево (обратный порядок).
6. Статистический график всегда ломаная линия или диаграмма.
4.1 Уровневые графики (гистограмма, полигон распределения)
Для таких графиков важно соблюдать два правила их построения:
1. Количественное значение группы должно следовать за изменением количественной характеристики признака (распространение признака по оси абсцисс первично).
2. При равных интервалах признака по оси ординат откладываются частоты, при неравных – плотность распределения.
Характерными представителями уровневых графиков являются гистограмма (рис.1) и полигон распределения.
Для общего вида гистограммы характерно следующее:
· предельная высота ограничена максимальной частотой, максимальной частостью или плотностью распределения;
· гистограмма характеризует не только интервалы распределения признака (основания прямоугольников), но и распределение объема признака для тех или иных интервалов (площадь прямоугольника);
· вид линии, ограничивающей гистограмму сверху, определяет ресурсы по объему признака;
· вся площадь прямоугольника S по максимальной высоте гистограммы для всего распределения признака характеризует матрицу объема признака.
Гистограмма наглядно иллюстрирует распределение признака, причем двояко:
· долей площади каждого прямоугольника
;
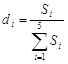· матрицей 
, где S – площадь матрицы.
Гистограмма показывает как изменяется объем признака. Для оценки изменений площади соседних прямоугольников суммируются (возможно нарастающим итогом) и эта сумма относится к общему объему признака (сумме площадей всех прямоугольников).
Правильно построенная гистограмма (в пределах установленных масштабов) позволяет выделить генеральную совокупность по объему признака прямым или обратным порядком. Прямой порядок выделения генеральной совокупности сопряжен с нарастающей динамикой объема признака (S1 + S2 + S3 + S4), обратный (S4 + S3 + + S2 + S1) – с убывающей.
Построить гистограмму можно только для интервального ряда распределения, и в этом состоит специфичность гистограммы.
Более универсальным является второй вид уровневого графика – полигон распределения. В дискретных рядах каждому определенному значению признака соответствует своя частота (частость), что отражается на оси абсцисс точками, а не интервалами, а по оси ординат – целыми значениями частоты или дробными частости. В этом случае полигон распределения будет представлен ломаной линией.
Для интервального ряда получение полигона распределения предполагает соединение середин верхней линии гистограммы.
Для смешанного ряда построение полигона распределения предполагает соединение середин верхних линий гистограмм с высотой дискретного значения признака.
Если есть возможность закодировать цифрами стандартную номенклатуру по атрибутивному признаку, то эти цифры могут быть зарегистрированы на оси абсцисс, и это позволит построить полигон распределения (так называемый кодовый полигон распределения).
Универсальность этих графиков снижает их потенциальные возможности по сравнению с гистограммами. Полигон также характеризует распределение признака, но не так конкретно, как гистограмма (затруднен процесс расчета всех площадей). Изменение объема признака регистрируется в целом и нарастающим итогом, поэтому полигон распределения не позволяет выделить генеральную совокупность.
Тем не менее, полигон распределения регистрирует точку или момент перехода количества в качество в процессе нарастания объема признака.
Похожие работы
... восприятии. Статистическим можно назвать лишь такое наблюдение, которое обеспечивает регистрацию устанавливаемых фактов в учетных документах для последующего их обобщения. Конкретными примерами статистического наблюдения служит систематическое собирание сведений, например на машиностроительных предприятиях о количестве произведенных машин и узлов, издержках производства, прибыли и т. д. ...
... котором ответы на изучаемые вопросы записываются со слов опрашиваемого. К опросу, например, прибегают при переписи населения. Однако, опрос может быть организован по разному. В статистическом наблюдении коммерческого права принято выделять следующие его виды: Þ Устный(экспедиционный) способ заключается в том, что специально подготовленные работники, которых обычно называют счетчиками, ...
... для малых предприятий всех организационно-правовых форм и форм собственности и годовая форма, содержащая показатели производственной деятельности этих предприятий. Общее руководство статистическим наблюдением за деятельностью коммерческих банков возложено на Банк России, который совместно с органами государственной статистики разрабатывает формы статистической отчетности и инструкции по их ...
... проведения наблюдения. Статистический формуляр - это учетный документ, который включает в себя адресную характеристику объекта наблюдения и статистические данные про него. Это могут быть переписные и отчетные листы, анкеты и т.п. Организационные вопросы статистического наблюдения Второй составляющей плана наблюдения являются организационные вопросы, которые определяют: органы и персонал ( ...
0 комментариев