Неформальное взвешивание при расчете статистических средних

8.3 Неформальное взвешивание при расчете статистических средних

При расчете статистических средних возможна процедура взвешивания неформального характера. В этом случае в качестве «веса» выбирается признак, функционально связанный с осредняемым. Кроме того, «веса» могут быть простыми (один признак) и сложными (произведение нескольких признаков, которое формирует общий признак, функционально связанный с осредняемым).

Процедура неформального взвешивания обязательна в следующих случаях:

1. Осредняемый признак качественный, т.е. расчет его предполагает использование плановых (стандартизованных) признаков. Например, осредняемые признаки включают содержание полезного компонента в руде, цену продаж, себестоимость, производительность труда. Простые «веса» используются при расчете средних содержаний полезного компонента, себестоимости, производительности труда. Сложные «веса» необходимо применять при расчете средних цен.

2. Осредняемые признаки качественные, комплексные по содержанию и интегральные по схеме образования. Например, для цены продаж «весом» должен быть количественный признак, причем комплексный, рассчитанный как произведение одного количественного признака, связанного с осредняемым прямой или технологической связью, и одного или двух качественных признаков, связанных с количественным признаком жесткой прямой связью. Если осредняемый признак интегрального содержания, то количественный признак должен быть жестко связан с модулем осредняемого признака, а один, два или три качественных признака находиться в функциональной связи с остальной частью осредняемого признака.

3. Количественные признаки с высокой долей качества (себестоимость ГРР, выручка, запасы полезного ископаемого). Для таких показателей «вес» может быть только сложным. В его состав входят два количественных признака и до трех качественных. Количественные показатели связаны функциональной (косвенной) связью с осредняемым признаком или формируют экономический фон существования осредняемого признака. Качественные показатели должны быть стандартными или цензовыми и связанными с количественными признаками.

Если результатом формального взвешивания является модуль средней, то в результате неформального взвешивания получают устойчивую (1-й случай) и прогрессивную (2-й и 3-й случаи) средние. От уровня средней зависят многие статистические расчеты и СОП. Поэтому в статистике существует набор приемов по оценке надежности (качества) средней.

Первая группа этих приемов предполагает сопоставление устойчивой и прогрессивной средней с модулем и детерминацию (ограничение) этого отклонения в зависимости от содержания признака. Для количественных признаков отклонение средней от модуля допустимо в диапазоне от 20 до 25 % в сторону увеличения и от 10 до 15 % в сторону снижения. Для качественных признаков устойчивая средняя может отклоняться от модуля от ±3 до ±7 %; прогрессивная в сторону увеличения в пределах 5-8 %, в сторону снижения 10-12 %.

Вторая группа приемов связана с расчетом специальных показателей (моды и медианы), которые позволяют быстро и надежно оценивать качество средних и уточнять их содержание.

Мода – это наиболее часто встречающееся значение признака в изучаемой совокупности (в ряду распределения). Таким образом, мода – это значение признака с максимальной частотой. В интервальном ряду выделяется модальный интервал (интервал с максимальной частотой). Мода в пределах этого интервала определяется или приближенно (середина интервала), или точно по формуле

где X_Мо – начальное значение интервала, содержащего моду; i_Мо и f_Мо – величина и частота модального интервала; f_Мо-1 и f_Мо+1 – частота интервала, предшествующего и следующего за модальным.

Медиана – это численное значение признака той единицы совокупности, которая стоит в середине ранжированного ряда (возрастающего). При нечетном числе единиц совокупности медиана – значение признака у четко регистрируемой середины совокупности. При четном числе единиц медианой является средняя арифметическая значений признаков у двух серединных единиц совокупности.

В интервальном ряду сначала аналогично описанной процедуре определяется медианный интервал. В пределах этого интервала медиана рассчитывается или упрощенно (середина интервала), или по формуле

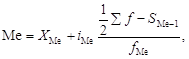
где X_Ме – начальное значение интервала, содержащего медиану; i_Ме – величина медианного интервала; Sf – сумма частот ряда; S_Ме-1 – сумма накопленных частот в интервалах, предшествующих медианному; f_Ме – частота медианного интервала.

Применение моды и медианы для оценки надежности (качества) средней зависит от характера ряда. Если значения моды, медианы и средней дискретного ряда совпадают, то средняя надежна и это модуль. Если мода и медиана попадают в другие уровни ряда, то возможны два случая:

· мода находится в предыдущем уровне, медиана – в нижнем уровне по отношению к средней. Это означает, что мы имеем надежную прогрессивную среднюю;

· мода находится в нижнем уровне, а медиана – в предыдущем. Полученная средняя не надежна.

Кроме сказанного возможно, что либо мода, либо медиана попадают в один интервал со средней. Если в один интервал со средней попадает мода, а медиана находится в предыдущем интервале, то получена надежная прогрессивная средняя. Если в один интервал со средней попадает медиана, а мода находится в нижнем интервале, то средняя не надежна.

Если мода, медиана и средняя интервального ряда попадают в один интервал, то получен модуль средней. Если мода и медиана попадают в другие уровни ряда, то возможны два случая:

· мода, медиана и средняя находятся в соседних уровнях. Имеет место надежная прогрессивная средняя;

· мода оказывается выше соседнего интервала*. Получена прогрессивная (стратегическая) средняя.

Если один из показателей (мода или медиана) попадает в один интервал со средней, а другой в соседний – результат аналогичен рассмотренному случаю для дискретного ряда.

Похожие работы

Статистические наблюдения

Скачать

21040

0

0

... восприятии. Статистическим можно назвать лишь такое наблюдение, которое обеспечивает регистрацию устанавливаемых фактов в учетных документах для последующего их обобщения. Конкретными примерами статистического наблюдения служит систематическое собирание сведений, например на машиностроительных предприятиях о количестве произведенных машин и узлов, издержках производства, прибыли и т. д. ...

Статистическое наблюдение в коммерческом праве

Скачать

38681

0

0

... котором ответы на изучаемые вопросы записываются со слов опрашиваемого. К опросу, например, прибегают при переписи населения. Однако, опрос может быть организован по разному. В статистическом наблюдении коммерческого права принято выделять следующие его виды: Þ   Устный(экспедиционный) способ заключается в том, что специально подготовленные работники, которых обычно называют счетчиками, ...

Сущность и методы статистического наблюдения

Скачать

59505

7

7

... для малых предприятий всех организационно-правовых форм и форм собственности и годовая форма, содержащая показатели производственной деятельности этих предприятий. Общее руководство статистическим наблюдением за деятельностью коммерческих банков возложено на Банк России, который совместно с органами государственной статистики разрабатывает формы статистической отчетности и инструкции по их ...

Статистическое наблюдение, первоначальная обработка и представление ее данных

Скачать

20196

0

1

... проведения наблюдения. Статистический формуляр - это учетный документ, который включает в себя адресную характеристику объекта наблюдения и статистические данные про него. Это могут быть переписные и отчетные листы, анкеты и т.п. Организационные вопросы статистического наблюдения Второй составляющей плана наблюдения являются организационные вопросы, которые определяют: органы и персонал ( ...