Навигация
ЗАДАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ
4. ЗАДАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ
ВАРИАНТ ПЕРВЫЙ
Задача 1
Имеются следующие отчетные данные 25 заводов одной из отраслей промышленности:
| Номер завода | Среднегодовая стоимость основных производственных фондов, млн. руб.@ | Валовая продукция в сопоставимых ценах, млн. руб. |
| 1 | 6,9 | 10,0 |
| 2 | 8,9 | 12,0 |
| 3 | 3,0 | 3,5 |
| 4 | 5,7 | 4,5 |
| 5 | 3,7 | 3,4 |
| 6 | 5,6 | 8,8 |
| 7 | 4,5 | 3,5 |
| 8 | 7,1 | 9,6 |
| 9 | 2,5 | 2,6 |
| 10 | 10,0 | 13,9 |
| 11 | 6,5 | 6,8 |
| 12 | 7,5 | 9,9 |
| 13 | 7,1 | 9,6 |
| 14 | 8,3 | 10,8 |
| 15 | 5,6 | 8,9 |
| 16 | 4,5 | 7,0 |
| 17 | 6,1 | 8,0 |
| 18 | 3,0 | 2,5 |
| 19 | 6,9 | 9,2 |
| 20 | 6,5 | 6,9 |
| 21 | 4,1 | 4,3 |
| 22 | 4,1 | 4,4 |
| 23 | 4,2 | 6,0 |
| 24 | 4,1 | 7,5 |
| 25 | 5,6 | 8,9 |
С целью изучения зависимости между среднегодовой стоимостью основных производственных фондов и выпуском валовой продукции произведите группировку заводов по среднегодовой стоимости основных производственных фондов, образовав пять групп заводов с равными интервалами. По каждой группе и совокупности заводов посчитайте:
1) число заводов;
2) среднегодовую стоимость основных производственных фондов – всего и в среднем на один завод.
3) стоимость валовой продукции всего и в среднем на один завод;
4) размер валовой продукции на один рубль основных производственных фондов (фондоотдачу).
Результаты представьте в виде групповой таблицы. Напишите краткие выводы.
Задача 2
Имеются следующие данные о заработной плате рабочих по цехам завода за два месяца.
| Номер цеха | январь | февраль | |||
| Средняя заработная плата, руб. | Фонд заработной платы, руб. | Средняя заработная плата, руб. | Численность рабочих, чел. | ||
| 1 | 4800 | 595200 | 4850 | 120 | |
| 2 | 5200 | 499200 | 5000 | 105 | |
Вычислите среднюю месячную заработную плату рабочих по заводу:
1) за январь;
2) за февраль.
Дайте характеристику динамике средней заработной платы рабочих по
каждому цеху и в целом по заводу.
Укажите, какой вид средней надо применять для вычисления этих показателей.
Задача 3
В целях изучения стажа рабочих завода проведена пятипроцентная бесповторная выборка, в результате которой получено следующее распределение рабочих по стажу работы:
| Стаж, число лет | Число рабочих, чел |
| До 6 6 – 12 12 – 18 18 – 24 свыше 24 | 15 25 35 15 6 |
На основе этих данных вычислите:
1) средний стаж рабочих завода;
2) средний квадрат отклонений (дисперсию) и среднее квадратическое отклонение;
3) коэффициент вариации;
4) с вероятностью 0,997 предельную ошибку выбранной средней, возможные границы, в которых ожидается средний стаж рабочих завода;
5) с вероятностью 0,954 предельную ошибку выборочной доли и границы удельного веса числа рабочих со стажем работы от 6 до 12 лет.
Задача 4
Имеются данные о полугодовой динамике поставки шерстяных тканей в розничную сеть области, млн. руб.:
Для анализа представленного динамического ряда определите:
1) цепной абсолютный прирост, темп роста и темп прироста.
2) определите среднемесячный темп роста поставки шерстяных тканей. Сделайте выводы.
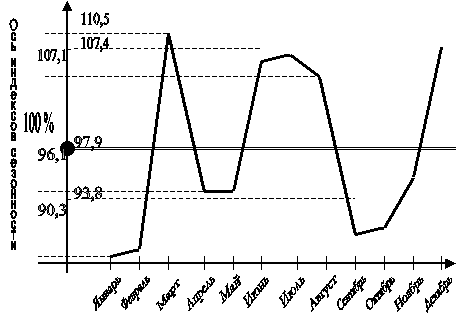
3) в целях анализа внутригодовой динамики и выявления общей тенденции развития определите индекс сезонности. Представьте графически сезонные волны развития данных явлений по месяцам.
| Месяцы | Объем поставки |
| Январь |
|
| Февраль |
|
| Март |
|
| Апрель |
|
| Май |
|
| июнь |
|
Задача 5
Остатки вкладов в сберегательных банках района одной из областей за первое полугодие характеризуются следующими данными, млн. руб.:
На 1 января – 10,3
На 1 февраля – 10,5
На 1 марта – 10,6
На 1 апреля – 10,8
На 1 мая – 11,3
На 1 июня – 11,6
На 1 июля – 11,8
Вычислите средний остаток вкладов:
1. за 1 квартал;
2. за 2 квартал;
3. за полугодие.
Поясните, почему методы расчета средних уровней рядов динамики в задачах 4, 5 различны.
Задача 6
Динамика средних цен и объема продажи на рынках города характеризуется следующими данными:
На основании имеющихся данных вычислите:
1. для рынка №1 (по двум видам товаров вместе):
а)общий индекс товарооборота;
б)общий индекс цен;
в)общий индекс физического объема товарооборота.
Определите в отчетном периоде прирост товарооборота и разложите по
факторам (за счет изменения цен и объема продажи товаров).
Покажите взаимосвязь между исчисленными индексами:
| Наименование товара | Продано товара, единиц | Средняя цена за единицу | ||
| Базисный период | Отчетный период | Базисный период | Отчетный период | |
| Рынок №1 | ||||
| Молоко, л | 600 | 550 | 10,5 | 12,5 |
| Творог, кг | 450 | 520 | 78 | 82 |
| Рынок №2 | ||||
| Молоко, л | 700 | 1000 | 10,0 | 12,9 |
2. Для двух рынков вместе (по молоку):
а)индекс цен переменного состава;
б)индекс постоянного состава;
в)индекс влияния изменения структуры объема продаж молока на динамику средней цены.
Объясните разницу между величинами индексов постоянного и переменного состава.
Задача 7
Имеются следующие данные о товарообороте магазина :
Товарная группа | Продано товаров в фактических ценах, тыс. руб. | Изменение цен в отчетном периоде по сравнению с базисным, % | |
| Базисный период | Отчетный период | ||
| Хлеб и хлебобулочные изделия | 120,5 | 211,2 | +4 |
| Кондитерские изделия | 30,4 | 54,6 | - 3 |
Вычислите:
1) общий индекс товарооборота в фактических ценах;
2) общий индекс цен и сумму экономии от изменения цен, полученную населением в отчетном периоде при покупке товаров в данном магазине;
3) общий индекс физического объема товарооборота, используя взаимосвязь индексов.
Задача 8
Для изучения тесноты связи между выпуском валовой продукции на один завод (результативный признак - y) и оснащенностью заводов основными производственными фондами (факторный признак - х) по данным задачи 1 вычислите коэффициент детерминации и эмпирическое корреляционное отношение. Поясните их значение.
ВАРИАНТ ВТОРОЙ
Задача 1
Имеются следующие отчетные данные 25 заводов одной из отраслей промышленности:
| Номер завода | Среднегодовая стоимость основных производственных фондов, млн. руб. | Валовая продукция в сопоставимых ценах, млн. руб. |
| 1 | 3,4 | 3,5 |
| 2 | 3,1 | 3,3 |
| 3 | 3,5 | 3,5 |
| 4 | 4,1 | 4,5 |
| 5 | 5,8 | 7,5 |
| 6 | 5,2 | 6,9 |
| 7 | 3,8 | 4,3 |
| 8 | 4,1 | 5,9 |
| 9 | 5,6 | 4,8 |
| 10 | 4,5 | 5,8 |
| 11 | 4,2 | 4,6 |
| 12 | 6,1 | 8,4 |
| 13 | 6,5 | 7,3 |
| 14 | 2,0 | 2,1 |
| 15 | 6,4 | 7,8 |
| 16 | 4,0 | 4,2 |
| 17 | 8,0 | 10,6 |
| 18 | 5,1 | 5,8 |
| 19 | 4,9 | 5,3 |
| 20 | 4,3 | 4,9 |
| 21 | 5,8 | 6,0 |
| 22 | 7,2 | 10,4 |
| 23 | 6,6 | 6,9 |
| 24 | 3,0 | 3,5 |
| 25 | 6,7 | 7,2 |
С целью изучения зависимости между среднегодовой стоимостью основных производственных фондов и выпуском валовой продукции произведите группировку заводов по среднегодовой стоимости основных производственных фондов, образовав пять групп заводов с равными интервалами. По каждой группе и совокупности заводов посчитайте:
5) число заводов;
6) среднегодовую стоимость основных производственных фондов – всего и в среднем на один завод.
7) Стоимость валовой продукции всего и в среднем на один завод;
8) Размер валовой продукции на один рубль основных производственных фондов (фондоотдачу).
Результаты представьте в виде групповой таблицы. Напишите краткие выводы.
Задача 2
Имеются следующие данные по зерновым культурам колхоза:
| Культура | В отчетном периоде | План на предстоящий период | ||
| Урожайность, ц/га | Валовой сбор, ц | Урожайность, ц/га | Посевная площадь, га | |
| Пшеница | 21,0 | 63000 | 23,0 | 3300 |
| Ячмень | 19,0 | 38000 | 20,0 | 1800 |
Вычислите среднюю урожайность зерновых культур по колхозу:
1) в отчетном периоде;
2) в планируемом периоде.
Укажите, какой вид средней надо применить для вычисления этих показателей и какие изменения урожайности предусмотрены в плане на предстоящий период.
Задача 3
В целях изучения норм расходования сырья при изготовлении продукции на заводе проведена десятипроцентная механическая выборка, в результате которой получено следующее распределение изделий по массе:
| Масса изделия, г | Число изделий, шт. |
| До 20 20 –21 21 –22 22 - 23 свыше 23 | 10 20 50 15 5 |
На основе этих данных вычислите:
1) среднюю массу изделия;
2) средний квадрат отклонений (дисперсию) и среднее квадратическое отклонение;
3) коэффициент вариации;
4) с вероятностью 0,954 предельную ошибку выборочной средней, возможные границы, в которых ожидается средняя масса изделий всей партии изготовленных изделий;
5) с вероятностью 0,954 предельную ошибку выборочной доли и границы удельного веса изделий с массой веса от 20 до 23 г.
Задача 4
Субсидии, полученные населением крупного города, характеризуются следующими данными:
Для анализа динамики субсидий, полученных населением за 1998-2004 гг., вычислите:
1) абсолютные приросты, темпы прироста по годам. Полученные данные представьте в таблице.
2) среднегодовой уровень субсидий.
3) среднегодовой абсолютный прирост субсидий.
4) среднегодовые темпы роста субсидий с 1998 по 2004 гг.
Изобразите динамику субсидий, полученных населением за 1998-2004 гг. на графике.
| Год | Субсидии, млн. руб. |
| 1998 | 190,0 |
| 1999 | 211,6 |
| 2000 | 242,2 |
| 2001 | 268,6 |
| 2002 | 284,8 |
| 2003 | 300,7 |
| 2004 | 306,5 |
Задача 5
Имеются следующие данные о товарных запасах торгового дома в третьем квартале, млн. руб.
| Группа товаров | На 1 июля | На 1 августа | На 1 сентября | На 1 октября |
| Продовольственные товары | 1,5 | 1,4 | 1,5 | 1,8 |
| Непродовольственные товары | 3,5 | 3,8 | 3,7 | 3,4 |
Вычислите среднеквартальный остаток:
1) продовольственных товаров;
2) непродовольственных товаров;
3) по обеим товарным группам вместе.
Поясните, почему методы расчета средних уровней рядов динамики в задачах 4, 5 различны.
Задача 6
Динамика себестоимости и объема производства продукции характеризуется следующими данными:
| Вид продукции | Выработано продукции, тыс.шт. | Себестоимость единицы продукции, тыс. руб. | ||
| Базисный период | Отчетный период | Базисный период | Отчетный период | |
| Ззавод №1 | ||||
| МП - 25 | 4,5 | 5,0 | 5,0 | 4,8 |
| ММ - 29 | 3,2 | 3,0 | 8,0 | 8,2 |
| Завод №2 | ||||
| МП - 25 | 10,6 | 10,0 | 7,0 | 6,6 |
На основании имеющихся данных вычислите:
1. для завода №1 (по двум видам продукции вместе):
а)общий индекс затрат на производство продукции;
б)общий индекс себестоимости продукции;
в)общий индекс физического объема производства продукции.
Определите в отчетном периоде изменение суммы затрат на производство продукции разложите по факторам (за счет изменения себестоимости и объема выработанной продукции).
Покажите взаимосвязь между исчисленными индексами:
2. Для двух заводов вместе (по продукции МП - 25):
а)индекс себестоимости переменного состава;
б)индекс себестоимости постоянного состава;
в)индекс влияния изменения структуры производства продукции на динамику средней себестоимости.
Объясните разницу между величинами индексов постоянного и переменного состава.
Задача 7
Имеются следующие данные о товарообороте магазина :
| Товарная группа | Продано товаров в фактических ценах, тыс. руб. | |
| 3 квартал | 4 квартал | |
| Мясо и мясопродукты | 136,8 | 150,4 |
| Молочные продукты | 261,2 | 253,6 |
В 4 квартале по сравнению с третьим кварталом цены на мясо и мясные продукты повысились в среднем на 5%, а на молочные остались без изменения.
Вычислите:
4) общий индекс товарооборота в фактических ценах;
5) общий индекс цен;
6) общий индекс физического объема товарооборота, используя взаимосвязь индексов.
Задача 8
Для изучения тесноты связи между выпуском валовой продукции на один завод (результативный признак - y) и оснащенностью заводов основными производственными фондами (факторный признак - х) по данным задачи 1 вычислите коэффициент детерминации и эмпирическое корреляционное отношение. Поясните их значение.
ВАРИАНТ ТРЕТИЙ
Задача 1
Имеются следующие отчетные данные 24 заводов одной из отраслей промышленности:
| Номер завода | Среднегодовая стоимость основных производственных фондов, млн. руб. | Валовая продукция в сопоставимых ценах, млн. руб. |
| 1 | 1,6 | 1,5 |
| 2 | 3,9 | 4,2 |
| 3 | 3,3 | 4,5 |
| 4 | 4,9 | 4,4 |
| 5 | 3,0 | 2,0 |
| 6 | 5,1 | 4,2 |
| 7 | 3,1 | 4,0 |
| 8 | 0,5 | 0,4 |
| 9 | 3,1 | 3,6 |
| 10 | 5,6 | 7,9 |
| 11 | 3,5 | 3,0 |
| 12 | 0,9 | 0,6 |
| 13 | 1,0 | 1,1 |
| 14 | 7,0 | 7,5 |
| 15 | 4,5 | 5,6 |
| 16 | 8,1 | 7,6 |
| 17 | 6,3 | 6,0 |
| 18 | 5,5 | 8,4 |
| 19 | 6,6 | 6,5 |
| 20 | 1,0 | 0,9 |
| 21 | 4,7 | 4,5 |
| 22 | 2,7 | 2,3 |
| 23 | 2,9 | 3,2 |
| 24 | 6,8 | 6,9 |
С целью изучения зависимости между среднегодовой стоимостью основных производственных фондов и выпуском валовой продукции произведите группировку заводов по среднегодовой стоимости основных производственных фондов, образовав пять групп заводов с равными интервалами. По каждой группе и совокупности заводов посчитайте:
1) число заводов;
2) среднегодовую стоимость основных производственных фондов – всего и в среднем на один завод.
3) стоимость валовой продукции всего и в среднем на один завод;
4) размер валовой продукции на один рубль основных производственных фондов (фондоотдачу).
Результаты представьте в виде групповой таблицы. Напишите краткие выводы.
Задача 2
Имеются следующие данные о квалификации рабочих двух бригад:
| № бригады | Число рабочих | Уровень квалификации каждого рабочего бригады (тарифный разряд) |
| 1 2 | 12 10 | 4; 3; 2; 4; 5; 6; 4; 3; 4; 3; 5; 4; |
| 3; 5; 6: 5; 4; 3; 2: 3; 3; 4; |
Определить средний уровень квалификации рабочих каждой бригады и двух бригад вместе.
Укажите, какой вид средней надо применять для вычисления этих показателей.
Задача 3
С целью изучения обеспеченности населения города предприятиями общественного питания проведена пятипроцентная механическая выборка, в результате которой получено следующие распределение предприятий общепита по числу посадочных мест:
| Группы предприятий по числу посадочных мест, ед. | Число предприятий, ед. |
| До 16 16 –32 32 –48 48 –64 свыше 64 | 15 20 25 8 5 |
На основе этих данных вычислите:
1) среднее число посадочных мест на одно предприятие;
2) средний квадрат отклонений (дисперсию) и среднее квадратическое отклонение;
3) коэффициент вариации;
4) с вероятностью 0,997 предельную ошибку выборочной доли и границы удельного веса числа предприятий с числом посадочных мест от 48 до 64.
Задача 4
Имеются данные о полугодовой динамике поставки бытовой техники в розничную сеть области, млн. руб.:
| Месяцы | Отчетный период |
| Июль | 132,4 |
| Август | 181,3 |
| Сентябрь | 127,8 |
| Октябрь | 119,4 |
| Ноябрь | 201,3 |
| Декабрь | 98,9 |
Для анализа представленного динамического ряда определите:
1. Цепной и базисный абсолютный прирост, темп роста и темп прироста.
2. Определите среднемесячный темп роста поставки тканей. Сделайте выводы.
3. В целях анализа внутригодовой динамики и выявления общей тенденции развития определите индекс сезонности. Представьте графически сезонные волны развития данных явлений по месяцам.
Задача 5
Имеются следующие данные об остатках товаров в розничном торговом предприятии:
| 1 января | 1 февраля | 1 марта | 1 апреля | 1 мая | 1 июня | 1 июля | |
| Остатки товара на начало месяца, тыс. руб. | 50,2 | 61,4 | 63,6 | 72,8 | 61,6 | 58,8 | 62,0 |
Вычислите среднемесячные остатки товаров:
1. за 1 квартал;
2. за 2 квартал;
3. за полугодие.
Поясните, почему методы расчета средних уровней рядов динамики в задачах 4, 5 различны.
Задача 6
Динамика себестоимости и объема производства продукции характеризуется следующими данными:
| Вид продукции | Выработано продукции, ед. | Себестоимость единицы продукции, тыс. руб. | ||
| Базисный период | Отчетный период | Базисный период | Отчетный период | |
| Завод №1 | ||||
| БМ – 40 | 2500 | 3000 | 14,0 | 13,0 |
| АН - 50 | 5000 | 6000 | 18,0 | 17,0 |
| Завод №2 | ||||
| БМ - 40 | 4000 | 5000 | 16,0 | 15,0 |
На основании имеющихся данных вычислите:
1. для завода №1 (по двум видам продукции вместе):
а)общий индекс затрат на производство продукции;
б)общий индекс себестоимости продукции;
в)общий индекс физического объема производства продукции.
Определите в отчетном периоде изменение суммы затрат на производство продукции разложите по факторам (за счет изменения себестоимости и объема выработанной продукции).
Покажите взаимосвязь между исчисленными индексами:
2. Для двух заводов вместе (по продукции БМ – 40):
а)индекс себестоимости переменного состава;
б)индекс себестоимости постоянного состава;
в)индекс влияния изменения структуры производства продукции на динамику средней себестоимости.
Объясните разницу между величинами индексов постоянного и переменного состава.
Задача 7
Имеются следующие данные о товарообороте магазина
| Товарная группа | Продано товаров в фактических ценах, тыс. руб. | |
| Базисный год | Отчетный год | |
| Одежда, белье, ткани | 1250,4 | 1480,2 |
| Обувь кожаная | 890,8 | 720,6 |
В отчетном годе по сравнению с базисным годом цены на одежду, белье, ткани повысились в среднем на 10%, а на кожаную обувь – на 8%.
Вычислите:
1. общий индекс товарооборота в фактических ценах;
2. общий индекс цен;
3. общий индекс физического объема товарооборота, используя взаимосвязь индексов.
4. Разложите по факторам прирост товарооборота магазина по данным товарным группам (за счет изменение цен и изменения количества проданных товаров).
Задача 8
Для изучения тесноты связи между выпуском валовой продукции на один завод (результативный признак - y) и оснащенностью заводов основными производственными фондами (факторный признак - х) по данным задачи 1 вычислите коэффициент детерминации и эмпирическое корреляционное отношение. Поясните их значение.
ВАРИАНТ ЧЕТВЕРТЫЙ
Задача 1
Имеются следующие отчетные данные 25 заводов одной из отраслей промышленности:
| Номер завода | Среднегодовая стоимость основных производственных фондов, млн. руб. | Валовая продукция в сопоставимых ценах, млн. руб. |
| 1 | 4,0 | 4,2 |
| 2 | 8,0 | 10,4 |
| 3 | 5,1 | 5,8 |
| 4 | 4,9 | 5,3 |
| 5 | 6,3 | 8,0 |
| 6 | 7,5 | 9,4 |
| 7 | 6,6 | 11,2 |
| 8 | 3,3 | 3,4 |
| 9 | 6,7 | 7,0 |
| 10 | 3,4 | 2,0 |
| 11 | 3,3 | 3,3 |
| 12 | 3,9 | 5,4 |
| 13 | 4,1 | 5,0 |
| 14 | 5,9 | 7,0 |
| 15 | 6,4 | 7,9 |
| 16 | 3,9 | 6,4 |
| 17 | 5,6 | 4,6 |
| 18 | 3,5 | 4,1 |
| 19 | 3,0 | 3,8 |
| 20 | 5,4 | 8,5 |
| 21 | 2,0 | 1,8 |
| 22 | 4,5 | 4,6 |
| 23 | 4,8 | 5,2 |
| 24 | 5,9 | 9,0 |
| 25 | 7,2 | 8,6 |
С целью изучения зависимости между среднегодовой стоимостью основных производственных фондов и выпуском валовой продукции произведите группировку заводов по среднегодовой стоимости основных производственных фондов, образовав четыре группы заводов с равными интервалами. По каждой группе и совокупности заводов посчитайте:
1) число заводов;
2) среднегодовую стоимость основных производственных фондов – всего и в среднем на один завод.
3) стоимость валовой продукции всего и в среднем на один завод;
4) размер валовой продукции на один рубль основных производственных фондов (фондоотдачу).
Результаты представьте в виде групповой таблицы. Напишите краткие выводы.
Задача 2
Имеются следующие данные о среднедневном товарообороте продавцов магазинов розничной торговой сети:
| Номер магазина | Торговый дом № 1 | Торговый дом №2 | ||
| Средний товарооборот продавца, руб. | Численность продавцов, чел. | Средний товарооборот продавца, руб. | Весь товарооборот, руб. | |
| 1. | 16000 | 54 | 12500 | 930000 |
| 2. | 18000 | 40 | 14000 | 1615000 |
Вычислите средний дневной товарооборот продавца:
1) по торговому дому №1.
2) по торговому дому № 2.
Укажите, в каком торге выше среднедневной товарооборот одного продавца и какой вид средней надо применить для вычисления этих показателей.
Задача 3
В целях изучения затрат времени на изготовление одной детали рабочими завода проведена десятипроцентная случайная бесповторная выборка, в результате которой получено следующее распределение деталей по затратам времени:
| Затраты времени за одну деталь, мин. | Число изделий, шт. |
| До 10 10-12 12-14 14-16 16 и более | 10 20 50 15 5 |
На основе этих данных вычислите:
1) средние затраты времени на изготовление одной детали;
2) средний квадрат отклонений (дисперсию) и среднее квадратическое отклонение;
3) коэффициент вариации;
4) с вероятностью 0,954 предельную ошибку выборочной средней, возможные границы, в которых ожидается средние затраты времени на изготовление одной детали на заводе;
5) с вероятностью 0,954 предельную ошибку выборочной доли и границы удельного веса числа деталей с затратами времени на их изготовление от 10 до 12 минут.
Задача 4
Урожайность овощей в области (по всем категориям хозяйств) характеризуется следующими данными:
Для анализа данного ряда динамики, вычислите:
1) абсолютные приросты, темпы роста, темпы прироста (цепные). Полученные показатели представьте в таблице.
2) среднегодовую урожайность овощей.
3) базисный темп роста с помощью взаимосвязи цепных темпов роста.
4) среднегодовой темп роста и прироста.
Год | Средняя урожайность, ц / га |
| 1998 | 150 |
| 1999 | 154 |
| 2000 | 162 |
| 2001 | 156 |
| 2002 | 180 |
| 2003 | 172 |
Изобразите урожайность овощей на графике. Сделайте выводы.
Задача 5
Имеются следующие данные о товарных запасах по одной из торговых организациях, млн. руб.:
| Группа товаров | Запасы товаров | ||||
| Базисный год | Отчетный год | Следующий год | |||
| На 01.01 | На 01.07 | На 01.01 | На 01.07 | На 01.01 | |
| Продовольственные товары | 8,0 | 9,2 | 7,8 | 12,4 | 13,2 |
| Непродовольственные товары | 24,0 | 29,0 | 26,2 | 32,6 | 26,4 |
Вычислите средние товарные запасы в базисном и отчетном году:
1.по продовольственным товарам;
Похожие работы
... соответственно; q1, q2 - объем отчетного, базисного периодов соответственно) для величины (цены) по каждому виду товара для величины q (объема) по каждому виду товаров: Найдем общие индексы по формулам: представляет собой среднее значение индивидуальных индексов (цены, объема), где j – номер товара. Общий индекс товарооборота равен: Найдем абсолютное ...
... экономико-рыночных отношений в нашей стране ставит перед школой новые задачи. Умение анализировать, сравнивать различные ситуации необходимо на сегодняшний день каждому современному человеку. Элективный курс «Общая теория статистики» с помощью математического аппарата даст начальные понятия о статистике, которые необходимы при решении управленческих задач. Курс рассчитан для учащихся 11 класса ...
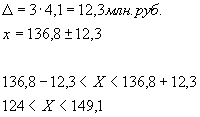
0 комментариев