Навигация
Ознакомить учащихся с принципом работы того или иного нового для них вычислительного алгоритма
1. Ознакомить учащихся с принципом работы того или иного нового для них вычислительного алгоритма.
2. Провести работу по отработке отдельных операций, входящих в новый алгоритм. Для формирования навыка выполнения данного алгоритма недостаточно отдельных упражнений, необходима тщательно продуманная их система, в которой должна соблюдаться последовательность упражнений с постепенным их усложнением. Однако следует предостеречь от излишнего числа однообразных упражнений в системе. Упражнения по формированию навыков должны быть достаточно разнообразными как по содержанию, так и по форме, лишь в этом случае достигается прочность навыков.
3. Провести работу по закреплению алгоритма – использовать его применение во всех стандартных и нестандартных ситуациях. Это немаловажно, так как уровень вычислительных навыков определяется систематичностью закрепления ранее усвоенных приемов вычислений и приобретением новых в связи с изучаемым материалом. Кроме того, формируемые навыки в выполнении вычислений и тождественных преобразований должны входить в ранее сформированную систему знаний, умений и навыков учащихся как составная часть. Поэтому после нескольких упражнений в формировании нового вычислительного умения или навыка полезно для достижения этой цели выполнять упражнения, связывающие изучаемое с ранее приобретенными умениями и навыками.
4. И, конечно же, необходимо провести проверку по усвоению алгоритма учащимися. Этому могут помочь проведение самостоятельных работ и наблюдения учителя за работой учащихся в классе. Анализ письменных и устных работ учащихся дает возможность установить, как усвоен данный материал, какие общие и наиболее характерные ошибки допущены при проведении вычислений, кто из учащихся и что именно не усвоил и как ликвидировать выявленные пробелы.
Вычислительные навыки и умения можно считать сформированными только в том случае, если учащиеся умеют с достаточной беглостью выполнять математические действия с натуральными числами, десятичными и обыкновенными дробями, рациональными числами, производить тождественные преобразования различных числовых выражений и приближенные вычисления, рационально организовывать ход вычислений, а также убеждать в правильности полученных результатов.
На каких же этапах урока и внеклассных мероприятий можно обучать вычислительным навыкам? На уроках можно отводить 5–10 минут, в течение которых учащиеся знакомятся с каким-либо алгоритмом и закрепляют его решением примеров. Пятиминутки «устного счета» так же могут быть использованы для формирования и отработки вычислительного навыка. На этапе актуализации знаний можно провести проверку знаний того или иного вычислительного алгоритма. А на внеклассных мероприятиях можно ввести специальное отделение, в котором учащиеся, хорошо владеющие вычислительными алгоритмами, с успехом выступают перед одноклассниками. Также можно использовать различные игровые приемы (конкурсы, состязания) для изучения, закрепления, проверки знания вычислительных алгоритмов.
Таким образом, вычислительные навыки нужны и при изучении программного материала в школе, и в повседневной жизни. Кроме того, они окажутся полезными для прикидки ожидаемого результата не только в учебной деятельности, но и в жизни. Именно поэтому учить учащихся быстро, правильно и рационально считать в школе необходимо и не только на уроках, но и на внеклассных занятиях по математике.
1.3 Устные вычисления как основа повышения вычислительной культуры школьниковВ методике математики различают устные и письменные приемы вычисления. К устным относят все приемы для случаев вычислений в пределах 100, а также сводящихся к ним приемы вычислений для случаев за пределами 100 (например, прием для случая 900·7 будет устным, так как он сводится к приему для случая 9·7). К письменным относят приемы для всех других случаев вычислений над числами большими 100.
Устная работа на уроках математики в младших классах, имеет большое значение – это и беседы учителя с классом или отдельными учениками, и рассуждения учащихся при выполнении тех или иных заданий и т.п. Среди этих видов устной работы можно выделить так называемые устные упражнения. Ранее они сводились в основном к вычислениям, поэтому за ними закрепилось название «устный счет». И хотя в современных учебниках содержание устных упражнений весьма разнообразно и велико, за счет введения алгебраического и геометрического материала, а также за счет большого внимания к свойствам действий над числами и величинами и других вопросов, название «устный счет» по отношению к устной форме проведения упражнений сохранилось до сих пор. Это, по мнению В.С. Кравченко, приводит к некоторым неудобствам, так как термин «устный счёт» используется, кроме того, и в своём естественном смысле, то есть вычисления, производимые устно, в уме, без записей. В связи с этим вместо термина «устный счёт», удобнее пользоваться термином «устные упражнения».
Как пишет педагог О.П. Зайцева в своей статье «Роль устного счета в формировании вычислительных навыков и развития личности ребенка» важность и необходимость устных упражнений доказывать не приходиться. Значение их велико в формировании вычислительных навыков и в совершенствовании знаний по нумерации, и в развитии личностных качеств ребёнка. Создание определённой системы повторения ранее изученного материала дает учащимся возможность усвоения знаний на уровне автоматического навыка. Устные вычисления не могут быть случайным этапом урока, а должны находиться в методической связи с основной темой и носить проблемный характер.
Для достижения правильности и беглости устных вычислений на каждом уроке математики необходимо выделять 5–10 минут для проведения упражнений в устных вычислениях, предусмотренных программой каждого класса.
Устные упражнения проводятся в вопросно-ответной форме, все учащиеся класса выполняют одновременно одни и те же упражнения. Устные упражнения важны и ещё и тем, что они активизируют мыслительную деятельность учащихся; при их выполнении активизируется, развивается память, речь, внимание, способность воспринимать сказанное на слух, быстрота реакции.
В сочетании с другими формами работы, устные упражнения позволяют создать условия, при которых активизируются различные виды деятельности учащихся: мышление, речь, моторика. И устные упражнения в этом комплекте имеют большое значение.
Так как устные упражнения или устный счёт это этап урока, то он имеет свои задачи:
1) воспроизводство и корректировка определённых ЗУН учащихся, необходимых для их самостоятельной деятельности на уроке или осознанного восприятия объяснения учителя;
2) контроль учителя за состоянием знаний учащихся;
3) психологическая подготовка учащихся к восприятию нового материала.
Так как уроки математики в младших классах как правило имеют кроме основной задачи, связанной с изучением текущего материала, еще ряд задач, относящихся к закреплению пройденного материала и подготовке к новым вопросам, то с этой точки зрения и подбираются упражнения к уроку, продумывается вид устных упражнений.
Для эффективного использования устных упражнений, нужно правильно определить их место в системе формирования понятий и навыков.
1.3.1 Приемы устного счета на уроках математикиУстные упражнения – неотъемлемая часть урока математики. Они могут проводится как вначале урока, так и на любом его этапе. Остановимся на устных упражнениях, проводимых в начале урока.
Наиболее часто устные упражнения – первый этап урока, причем не только в 5–6-х, но и в старших классах.
Цель этого этапа: во-первых, подготовить учащихся к продуктивной работе на всем протяжении урока, значит, среди этих упражнений должны быть задания на восстановление опорных заданий и умений. Во-вторых, постоянно проводить работу по поддержанию и совершенствованию ранее сформулированных знаний и умений, в частности, вычислительных навыков. И, в-третьих, способствовать развитию учащихся, т.е. необходимо на каждом уроке предлагать задачи, требующие сообразительности, внимания, анализа и обобщения имеющихся знаний и т.п.
В 5–6 классах для развития и совершенствования вычислительных навыков часто используются так называемые цепочные вычисления.
В учебнике Н.Я. Виленкина и др. такие цепочки даются в виде схем и в виде столбиков. Роль этих упражнений не сводится только к поддержанию умения считать. Важно, что они хороши для развития оперативной памяти, тренировки внимания, настойчивости. Вообще, в учебниках 5–6 классов Н.Я. Виленкина и др. такие примеры достаточно разнообразны для применения их в устном счете.
При проведении устного счета сталкиваешься с такой проблемой, как охват всех учащихся. При наполняемости классов в 25 человек сделать это довольно проблематично. Как правило, классы по силам неоднородны, сильные ученики выполняют все упражнения довольно быстро, что приводит к тому, что постоянно отвечают одни и те же, или им становится скучно. Другие же ученики имеют возможность вообще не выполнять устные упражнения, либо выполнять их от случая к случаю. Смысл же заданий устного счета в том, чтобы каждый ученик выполнил весь объем вычислений, а учитель имел возможность быстро и легко проверять работу учащихся.
Поэтому при планировании устной работы в начале урока можно поступить следующим образом: на доске выписываем пример из методического пособия «Упражнения для быстрого счета» на интересующие разделы и темы, предназначенные для устного счета или текстом, иногда по вариантам, иногда одинаковые. Учащимся дается определенное количество времени, в зависимости от количества заданий. Все вычисления и рассуждения учащиеся производят устно, записывая только конечные результаты, причем именно в той последовательности, в какой были предложены задания (это нужно для облегчения проверки). Через отведенное время собираем по 4–5 тетрадей с каждого варианта. Потом вызываем ученика на каждое задание, который называет только ответы, при необходимости или затруднении обсуждаем или комментируем. Одновременно проверяем сданные тетради, с выставлением отметок.
Так как ученики заранее не знают, чьи тетради берем на проверку, это активизирует их действия, заставляет работать каждого. Такую работу можно проводить во всех классах.
Кроме того, можно использовать следующую форму работы, которая применима в тех ситуациях, когда требуется «набить руку» по темам:
1) упрощение выражений;
2) формулы сокращенного умножения;
3) решение простейших тригонометрических уравнений и неравенств, и др.
Берем одинарный лист в клетку и складываем его по длине пополам. Получаем 4 страницы. В течение 4-х уроков, каждый ученик получает один из четырех вариантов (каждый раз новый) одной и той же работы. Задание выполняется устно, записываются только ответы. Новый вариант работы выполняется на новой странице. Обычно берется 10 заданий в каждом варианте, которые охватывают все возможные случаи для данной темы. Учащимся дается ограниченное количество времени. После каждого урока работы проверяются и оцениваются. На следующем уроке выдаются эти же листочки и другой вариант работы. В журнал выставляется итоговая отметка по результатам всех четырех работ. Такой вид работы позволяет к четвертому уроку существенно увеличить процент качества выполнения работ.
1.3.2 Виды упражнений для устного счета
Навыки устных вычислений формируются в процессе выполнения учащимися разнообразных упражнений. Рассмотрим основные их виды [1].
1) Нахождение значений математических выражений.
Предлагается в той или иной форме математическое выражение, требуется найти его значение. Эти упражнения имеют много вариантов. Можно предлагать числовые математические выражения и буквенные (выражение с переменной), при этом буквам придают числовые значения и находят числовое значение полученного выражения, например:
· найдите разность чисел 100 и 9;
· найдите значение выражения ![]() , если С = 100, К = 9.
, если С = 100, К = 9.
Выражения могут предлагаться в разной словесной форме:
· из 100 вычесть 9; 100 минус 9;
· уменьшаемое 100, вычитаемое 9, найдите разность;
· найти разность чисел 100 и 9;
· уменьшить 100 на 9 и т.д.
Эти формулировки использует не только учитель, но и ученики.
Выражения могут включать одно и более действий. Выражения с несколькими действиями могут включать действия одной ступени или разных ступеней, например:
· 47 + 24![]() ;
;
· 72: 12 · 9.
Могут быть действия со скобками или без скобок: (![]() ): 3,
): 3, ![]() : 3. Как и выражения в одно действие, выражения в несколько действий имеют разную словесную формулировку, например:
: 3. Как и выражения в одно действие, выражения в несколько действий имеют разную словесную формулировку, например:
· из 90 вычесть частное чисел 42 и 3;
· уменьшаемое 90, а вычитаемое выражено частным чисел 42 и 3.
Выражения могут быть заданы в разной области чисел: с однозначными числами, с двузначными, с трехзначными и т.д., с натуральными числами и величинами. Однако, как правило, приёмы устных вычислений должны сводиться к действиям над числами в пределах 100. Так, случай вычитания четырехзначных чисел сводится к вычитанию двузначных чисел и, значит, его можно предлагать для устных вычислений.
Выражения можно давать и в форме следующей таблицы
| Уменьшаемое | 12 | 14 | 35 | 12 | 28 |
| Вычитаемое | 10 | 8 | 15 | 5 | 10 |
| Разность |
Основное значение упражнений на нахождение значений выражений – выработать у учащихся твердые вычислительные навыки, а также они способствуют усвоению вопросов теории арифметических действий.
2) Сравнение математических выражений.
Эти упражнения имеют ряд вариантов. Могут быть даны два выражения, а надо установить, равны ли их значения, а если не равны, то какое из них больше или меньше: 6 + 4 * 4 + 6, 20 + 7 * 20 + 5, 20 · 8 * 18 · 10, 8 · 9 * 8 · 10. Вместо * необходимо поставить знак <, > или =.
Могут предлагаться упражнения, в которых уже дан знак отношения и одно из выражений, а другое выражение надо составить или дополнить:
8 · (10 + 2) = 8 · 10 +…
Выражения таких упражнений могут включать различный числовой материал: однозначные, двузначные, трехзначные числа и величины. Выражения могут быть с разными действиями.
Главная роль таких упражнений – способствовать усвоению теоретических знаний об арифметических действиях, их свойствах, о равенствах, о неравенствах и др. Также они помогают выработке вычислительных навыков.
3) Решение уравнений.
Это прежде всего простейшие уравнения (х + 2 = 10) и более сложные.
Уравнение можно предлагать в разных формах:
· решение уравнения 24: х = 3;
· из какого числа надо вычесть 18, чтобы получить 40?
· найдите неизвестное число: 73 + х = 73 + 18
· я задумала число, умножила его на 5 и получила 85. Какое число я задумала?
Назначение таких упражнений – выработать умение решать уравнение, помочь учащимся усвоить связи между компонентами и результатами арифметических действий.
4) Решение задач.
Для устной работы предлагаются и простые и составные задачи.
Эти упражнения включаются с целью выработки умений решать задачи, они помогают усвоению теоретических знаний и выработке вычислительных навыков.
Разнообразие упражнений возбуждает интерес у детей, активизирует их мыслительную деятельность.
1.3.3 Формы восприятия устного счетаВ применении устного счета можно выделить несколько форм.
1) Беглый слуховой (читается учителем, учеником, записано на магнитофоне) – при восприятии задания на слух большая нагрузка приходится на память, поэтому учащиеся быстро утомляются. Однако такие упражнения очень полезны: они развивают слуховую память.
2) Зрительный (таблицы, плакаты, записи на доске, счеты, диапозитивы) – запись задания облегчает вычисления (не надо запоминать числа). Иногда без записи трудно и даже невозможно выполнить задание. Например, надо выполнить действие с величинами, выраженными в единицах двух наименований, заполнить таблицу или выполнить действия при сравнении выражений.
3) Комбинированный.
Так же применяются:
– обратная связь (показ ответов с помощью карточек);
– задания по вариантам (обеспечивают самостоятельность);
– упражнения в форме игры (молчанка, продолжи цепочку, стук-стук, хлопки).
Таким образом, при формировании и развитии математических навыков учащихся значимое место занимают вычислительные навыки и, в частности, устные вычисления.
2. Методика повышения вычислительной культуры школьников 2.1 Организация устных вычислений учащихся
Чтобы навыки устных вычислений постоянно совершенствовались, необходимо установить правильное соотношение в применении устных и письменных приёмов вычислений, а именно: вычислять письменно только тогда, когда устно вычислять трудно.
Упражнения в устных вычислениях должны пронизывать весь урок. Их можно соединять с проверкой домашних заданий, закреплением изученного материала, предлагать при опросе. Особенно хорошо, если наряду с этим, специально отводить 5–7 минут на уроке для устного счёта. Материал для этого можно подобрать из учебника или специальных сборников. Устные упражнения должны соответствовать теме и цели урока и помогать усвоению изучаемого на данном уроке или ранее пройденного материала. В зависимости от этого учитель определяет место устного счета на уроке. Если устные упражнения предназначаются для повторения материала, формированию вычислительных навыков и готовят к изучению нового материала, то лучше их провести в начале урока до изучения нового материала. Если устные упражнения имеют цель закрепить изученное на данном уроке, то надо провести устный счет после изучения нового материала. Не следует проводить его в конце урока, так как дети уже утомлены, а устный счет требует большого внимания, памяти и мышления. Количество упражнений должно быть таким, чтобы их выполнение не переутомляло детей и не превышало отведенного на это времени урока.
При подборе упражнений для урока следует учитывать, что подготовительные упражнения и первые упражнения для закрепления, как правило, должны формироваться проще и прямолинейнее. Здесь ненужно стремиться к особенному разнообразию в формулировках и приёмах работы. Упражнения для отработки знаний и навыков и, особенно, для применения их в различных условиях, наоборот должны быть однообразнее. Формулировки заданий, по возможности должны быть рассчитаны на то, чтобы они легко воспринимались на слух. Для этого они должны быть чёткими и лаконичными, сформулированы легко и определённо, не допускать различного толкования. В случаях, когда задания всё-таки трудны для усвоения на слух, необходимо прибегать к записям или рисункам на доске. Устный счет на уроках математики способствует развитию и формированию прочных вычислительных навыков и умений, он также играет немаловажную роль в привитии и повышении у детей познавательного интереса к урокам математики как одного из важнейших мотивов учебно-познавательной деятельности, развития логического мышления, развития личностных качеств ребенка.
Рассмотрим часто встречающиеся случаи умножения и деления, в которых особенно плодотворно применение устного счета.
2.1.1 Дроби1. Умножение целого числа на смешанное. Умножение целого числа на смешанное число может быть выполнено по правилу умножения числа на сумму, так как смешанное число есть сумма целого числа и дроби. Поясним это на числовом примере:
1) ![]() .
.
Но при умножении целого числа на смешанное число можно обратить смешанное число в неправильную дробь, затем умножить целое число на числитель неправильной дроби, полученное произведение сделать числителем искомого произведения, знаменатель же произведения оставить знаменатель множителя:
![]() .
.
Как видим, первый способ проще и дает возможность быстрее производить умножение.
2) ![]() .
.
Преимущество первого способа перед вторым в данном примере очевидно. Но могут быть случаи, когда проще и быстрее можно решить пример вторым способом:
3)![]() .
.
Таким образом, при умножении целого числа на смешанное число надо внимательно рассмотреть пример и применить тот способ, который в данном случае быстрее ведет к цели.
2. Деление смешанного числа на целое. Смешанное число можно рассматривать как сумму двух чисел. Следовательно, деление смешанного числа на целое есть деление суммы двух чисел на число. Чтобы разделить сумму чисел на число, достаточно разделить на это число каждое из слагаемых, и сложить полученные результаты.
Мы знаем, что все основные законы арифметических действий, установленные для натуральных чисел, сохраняют свою силу и для дробных чисел:
1) 348![]() : 4 = (348 +
: 4 = (348 + ![]() ): 4 = 348: 4 +
): 4 = 348: 4 + ![]() : 4 = 87 +
: 4 = 87 + ![]() = 87
= 87![]() .
.
Как видим, этот способ гораздо легче (он дает возможность быстрее производить вычисления), чем обычный способ деления смешанного числа на целое с образованием смешанного числа в неправильную дробь.
2) 252![]() : 12 = (252 +
: 12 = (252 + ![]() ): 12 = 252: 12 +
): 12 = 252: 12 + ![]() : 12 = 21 +
: 12 = 21 + ![]() = 21
= 21![]() .
.
3. Умножение и деление целого числа на дробь, которая отличается от единицы на одну долю:
а) умножение
1) ![]() ;
;
2) ![]() ;
;
б) деление
3) ![]() .
.
Рассмотрим пример деления целого числа на дробь, причем дробь отличается от единицы на две и более долей:
1) ![]() .
.
Как мы видим, данный способ дает возможность быстрее умножать и делить целое число на дробь, чем обычный способ, а поэтому следует разобранный способ использовать при умножении или делении целого числа на дробь.
2.1.2 ПроцентыУстное нахождение процентов числа и числа по данным его процентам
Устное нахождение 5%, 25%; 12,5% числа и т.п., а также числа по данным его процентам основано на умножении и делении на дроби 0,05; 0,25; 0,125 и т.п.
а) Нахождение процента от числа.
1) Найти 25% от 468.
![]() . Но можно заменить 25% и обыкновенной дробью. Этот пример можно решить так:
. Но можно заменить 25% и обыкновенной дробью. Этот пример можно решить так: ![]() .
.
2) Найти 12,5% от 728.
![]() Можно 12,5% заменить обыкновенной дробью:
Можно 12,5% заменить обыкновенной дробью: ![]() .
.
б) Нахождение числа по данным его процентам.
Найти число, если 5% его равны 492.
![]() .
.
Как видим, способ замены процентов обыкновенной дробью иногда дает возможность быстрее производить вычисления, чем умножением на десятичную дробь.
2.1.3 Нахождение квадратов числаПохожие работы
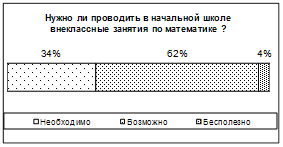
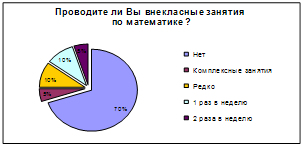
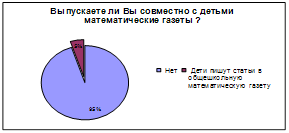
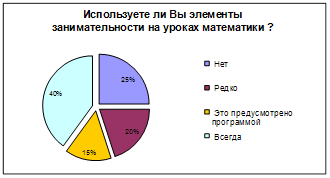
... и младших школьников. Анкета для студентов включала в себя два вопроса, один из которых о том, в чем, по их мнению, заключается развитие математических способностей школьников, а второй ¾ для выяснения отношения студентов к проведению внеклассной работы по математике в начальных классах. Анкета для преподавателей имела своей целью выяснить, проводят ли (а если проводят, то как часто) учителя ...
... курс «Решение уравнений и неравенств с использованием свойств функций» Глава II. Разработка элективного курса «Решение уравнений и неравенств с использованием свойств функций» §1. Методические основы разработки элективного курса Пояснительная записка. Основная задача обучения математике в школе – обеспечить прочное и сознательное овладение учащимися системой математических знаний и ...
... виртуальными объектами. Реализация этого принципа основывается на использовании творческих сред, таких как, например, Лого, Кумир, Роботландия [11]. Глава 2. Методика использования дистанционных технологий как средство развития алгоритмической культуры школьников на уроках информатики 2.1 Возможности использования дистанционных технологий на уроках информатики Дистанционное обучение – ...
... при ошибке в его выборе, учитывать по уровневый подход. 4. Математика должна входить в набор обязательных учебных предметов любого из профилей.2 МАТЕМАТИЧЕСКИЙ ФАКУЛЬТАТИВ КАК ВЕДУЩАЯ ФОРМА ПРОФИЛЬНОГО ОБУЧЕНИЯ МАТЕМАТИКЕ В ОБЩЕОБРАЗОВАТЕЛЬНОЙ ШКОЛЕ2.1. Организационно-педагогические условия успешного функционирования математических факультативов Еще на рубеже XIX и XX вв. некоторые ...
0 комментариев