А + 0 = а; 3. а • 0 = 0;

1. а + 0 = а; 3. а • 0 = 0;

2. а + b' я (а + b)' 4. а • b' = а ' b + а . Следствие: а + 1 = а' . Следствие: а • 1 =5 а .

Аксиомы 1 и 3 и следствия из этих аксиом ученики должны твердо знать Нахождение результата сложения (до таблиц сложения) определяется путем присчитывания по одному (т.е. используется первое следствие).

Нахождение результата умножения в начальных классах нельзя рассматривать с позиции аксиом 3 и 4. Поэтому в традиционной методике умножение рассматривается как частный случай сложения, что позволяет умножать натуральные числа только начиная с двух. Естественно, такой подход к операции умножения нельзя считать удачным, так как не позволяет найти результат умножения в таких случаях, как а • 1; а - 0;

(а/b) • (с/а).

В разделах I и III достаточно подробно рассмотрена операция умножения как мощность декартова произведения и как сумма одинаковых величин. Существует и другой подход к операции умножения, с позиции которого можно обосновать не только умножение натуральных чисел, начиная с двух, но и умножение на 1 и на 0, умножение обыкновенных дробей. Этот подход заключается в том, что умножение рассматривается как переход от одной единицы измерения к другой Сформировать у учащихся смысл операции умножения с этой позиции можно на таких практических работах.

Пример 1. Нужно измерить емкость банки сначала кружками, а потом стаканами (рис. 2.18). В ходе измерения получили 5 кружек или 15 стаканов. Учитель обращает внимание на то, что стаканами измерять долго, и задает

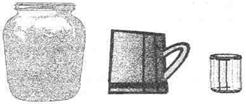
Рис. 2.18

вопрос: "Нельзя ли узнать, не измеряя, сколько стаканов в банке?" Дети предлагают для этого измерять стаканами кружку. Так как в банке 5 кружек (старая мерка) и в одной кружке 3 стакана (новая мерка), то в банке 5 • 3 = 15 (стаканов).

Пример 2. Учитель предлагает быстро пересчитать тетради. Ученики считают по две тетради (старая мерка) и получают 15 пар, поэтому в пачке 15 - 2 = 30 (тетрадей).

Пример 3. Ученикам предлагается быстро измерить полоску и даются две мерки: в 1 дм и в 1 см Дети меряют сначала большой меркой и получают число 4. Так как 1 дм содержит 10 см (новая мерка 1 см), то вся полоска содержит 4 • 10 = 40 (см).

Пример 4. Задача. Сколько нужно плиток кафеля, чтобы обложить такую же стенку, которая изображена на рис. 31? Дети считают сначала рядами (1 ряд -старая мерка), а потом -сколько в ряду плиток (1 плитка - новая мерка). Всего плиток 4 • 9 = 36. •

Умножение на 1 можно объяснить так: пусть в примере 1 в кружке помещается ровно один стакан, тогда в банке будет 5 • 1 = 5 (стаканов).

Умножение на 0 можно объяснить на примерах, в которых новая мерка значительно больше старой мерки и измеряемой величины.

Нахождение результата вычитания основывается на следующем определении.

Определение. Разностью из натурального числа " а " натурального числа " b " называется такое натуральное число " с ", что а = b + с.

Таким образом, вычитание рассматривается как действие обратное сложению. Это позволяет находить результат вычитания не только путем отсчитывания по одному, но и используя зависимость между компонентами операции сложения: 5 - 2 = (5 - 1) -1 и 2 + П =5.

Нахождение результата деления основывается на следующем определении.

Определение. Частным от деления натурального числа " а" на натуральное неравное нулю число " b " называется такое натуральное число " с ", что а • b == с.

Так как деление есть операция обратная умножению, то для нахождения результата деления используется зависимость между компонентами операции умножения: 3 •П=6. На этом же основывается и составление таблиц вычитания и деления:

а) 2+3=5; 5 - 2=3; . б) 2 • 3 = 6; 6:2=3.

Деление с остатком в начальных классах основывается на следующем определении.

Определение. Делением натурального числа " а " на натуральное число «b» с остатком называется отыскание такого частного q и остатка г , что а = b • q + г, где г < b.

Согласно этому определению, наряду с записью, например, 23 : 5 = 4 (остаток 3), ученикам должна даваться и такая запись: 23 = 5 • 4 + 3. Это

позволяет разнообразить примеры на деление с остатком: П =5*4+3 (проверка деления с остатком); 23 = П • 4 + П; 23 == 5 • О + О. Ученик + О. Учеников должны знать не только порядковую структуру множества натуральных чисел, которая была приведена выше, но и алгебраическую структуру натуральных чисел. Приведем ее.

1. В множестве натуральных чисел всегда выполнима операция сложения.

2. В множестве натуральных чисел всегда выполнима операция умножения.

3. а + b = b + а (переместительное свойство сложения).

4. а • b = b • а (переместительное свойство умножения).

5. (а + b) +с = а + (b +с) (сочетательное свойство сложения).

6. (а • b) • с =а • (b • с) (сочетательное свойство умножения).

7. (а+b) • с =а *с+b *с (распределительное свойство умножения относительно сложения).

8. а + 0 = а.

9. а • 0 = 0.

10.а + 1 = а'.

11. а • 1= а.

Операции над многозначными числами основываются на позиционной системе счисления.

Определение. Счислением (нумерацией) называется совокупность способов устного наименования и письменного обозначения чисел.

Существуют непозиционные и позиционные системы счисления.

В непозипионной системе счисления каждый знак (цифра) служит для обозначения одного и того же числа. Примером непозиционной системы счисления является римская нумерация, которой широко пользуются в настоящее время. Например, XII - это 10 + 1 + 1 =12.

Позиционная система счисления базируется на поместном значении цифр, заключающееся в том, что один и тот же знак (цифра) означает одно и то же число единиц разных разрядов независимо от того, на каком месте в записи числа стоит этот знак. Например, в числе 737 цифра 7 означает числа семь и семьсот.

Изучение темы "Нумерация чисел" учитель должен начинать с формирования представления о позиционной системе счисления, в которой дети не только знакомятся с существованием систем счисления с разными основаниями, но и понимают необходимость существования позиционной системы счисления. Это можно осуществить в ходе такой практической работы.

Пример 1. Дается задание измерить достаточно большой отрезок маленькой меркой (рис. 2.19). Дети уже знают, что лучше взять для измерения большую мерку, им предлагается тогда мерка, которая содержит 41маленьких мерки (большая мерка может содержать какое угодно число маленьких мерок, но обязательно целое их число). Ученики получили, например, что большая мерка поместилось 3 раза, а в остатке поместилось 2 маленькие мерки. В результате у них получилось число 32 с основанием системы счисления 4.

Рис. 2.19

В зависимости от длины измеряемого отрезка можно брать для измерения большие мерки, которые содержат по 2, 3, 4, 5, ... маленьких мерок. Тем самым, ученики приходят к выводу, что существуют позиционные системы счисления с различными основаниями. Далее можно провести беседу о существовании в практической деятельности человека систем счисления с основанием 7 (число дней в неделе), 12 (число месяцев в году), 100 (число лет в веке), 60 (число минут в часе) и т. д.

В традиционном обучении при изучении нумерации чисел у учащихся отрабатываются понятия "десятки", "сотни", что приводит к смешению устной нумерации и письменной. Этого нельзя делать, потому, что это может привести к ошибкам. Например, дети часто говорят, что в числе 325 два десятка (вместо - 32 десятка), В дальнейшем это приводит к затруднениям в выполнении операций над многозначными числами, которые базируются на операциях над однозначными числами. Поэтому при изучении многозначных чисел нужно обращать внимание детей на разряды и на число единиц в разрядах. Например, в числе 6325 шесть единиц четвертого разряда, три единицы третьего разряда, две единицы второго разряда и пять единиц первого разряда. Такая работа позволит ученикам легче и быстрее усвоить операции над многозначными числами, которые производятся над разрядами. Законы операций над многозначными числами должны использоваться учителем для формирования вычислительных навыков.

VI. Числовые выражения. Числовые равенства и неравенства, их свойства

Любое число уже является числовым выражением. Если А и В -числовые выражения, то А + В, А - В, А • В, А : В также являются числовыми выражениями. Выполнив операции; которые имеют место в числовом выражении, получают значение числового выражения. Существуют выражения, которые не имеют значения. Например, выражение 28 ; 8 - 44 не имеет числового значения.

С первых дней пребывания в школе дети сталкиваются с различными числовыми выражениями и учатся находить их числовое значение. Значительно меньше в школе уделяется внимание числовым равенствам и неравенствам, их свойствам, что сказывается при их обучении в старших классах. Поэтому учитель должен предлагать учащимся достаточное количество упражнений следующих видов.

1. Являются ли данные равенства верными:

10-3*2=2*2; 5+2*3=6+4?

2. Являются ли данные неравенства верными:

8-3 • 2<3 +4; 14: (5 + 2) >2 + 3 ?

3. Зная, что 2 + 3 = 10 : 2 и 4 +7 > & + 2, поставьте вместо звездочки знак " - ", " > ", " < ", не вычисляя значения числовых выражений, стоящих в правой и левой частях числовых равенств и неравенств:

(2 + 3) + 4 * 10 : 2 + 4 ; (2 + 3) - 4 *10 : 2 - 4 ;

(2 + 3) • 3 * (10 : 2) • 3 ; 4+7-3*8+2-3;

(4 + 7) • 2 • (8 + 2) • 2 .

VII. Выражение с переменными, его область определения

Если числовое выражение содержит и буквы, то мы имеем выражение с переменными. Например, 2а - 3 ; За + 2b с + 8 .

Выражение с переменными обычно обозначают так: f(х); А(b;с); В(х;у) Если в выражение с переменными подставить вместо букв их значения, то получится числовое выражение.Те значения переменной, при которых выражение с переменной имеет числовое значение, называется областью определения выражения с переменной. Например, областью определения выражения с переменной 2а - 3 на множестве действительных чисел является все множество действительных чисел, а на множестве натуральных чисел - натуральные числа, начиная с двух (если а = 1 , то 2 • 1 - 3 не является натуральным числом).

В начальных классах учитель обязан сформировать понятие о выражении с переменной и его области определения. Покажем на примерах, как это можно сделать.

Пример 1. Цель; сформировать у детей понимание необходимости введения в числовое выражение букв и представление об области определения выражения с переменной.

Учитель записывает на доске несколько числовых выражений: 1 + 2; 2+2; 3+2; 4+2. Затем он обращает внимание на то, что первое слагаемое меняется, а второе - нет. Поэтому, чтобы не продолжать ряд,

можно все эти выражения заменить одним П+ 2, где в окошечко можно подставить любое натуральное число. Учитель предлагает в окошечко подставить числа 1 ; 2 ; 3 ; 4 ; 5 и найти значение получившихся числовых выражений. Здесь область определения задана учителем.

Пример 2. Цель: научить учащихся самим находить область определения выражения с переменной.

Учитель спрашивает, какие числа можно подставить в следующие выражения: 8 - П; 3-2; П : 2; 5 – П : 3; П : 5 - 7. Дети подбором находят область определения каждого выражения с переменной.

Пример 3. Цель: научить учащихся находить область определения выражения с переменной в задачах.

Учитель предлагает следующую задачу. Сколько килограммов сахара, расфасованного в пакеты, принесли Коля и Оля, если в каждом пакете по два килограмма сахара?

Ученики записывают задачу в виде выражения 2а + 2b (или 2 • (а + b)), где а - количество пакетов, которые принес Коля, и b - количество пакетов, которые принесла Оля. Затем в ходе анализа задачи дети делают вывод, что Коля может нести не более 8 кг (от одного до четырех пакетов), а Оля - не более 6 кг (от одного до трех пакетов). Таким образом, ае{1;2;3;4} и

b е { 1; 2; 3}.

Задача имеет 12 решений, если перебрать все варианты наборов а и b .

VIII. Уравнения и неравенства, область определения, множество решений. Свойства уравнений и неравенств

Равенство (неравенство), содержащее неизвестное, называется уравнением (неравенством). Множество, элементы которого можно подставить в уравнение (неравенство) вместо неизвестного, называется областью определения уравнения (неравенства).

Те значения неизвестного из области определения, при которых уравнение (неравенство) обращается в верное числовое равенство (неравенство), называется корнями уравнения (множеством решения неравенств).

Если область определения уравнения (неравенства) не задана, то она совпадает с областью определения выражений, входящих в данное уравнение (неравенство). Например, областью определения уравнения (3 х2): х • 2 = 4 является множество (- °о; 0) U(0;оо).

Два уравнения (неравенства) называются равносильными, если у них совпадают области определения и множества решений.

Например, уравнения (3 х2 ) : х - 2 = 4 (1) и 3 х - 2=4 (2) не равносильны, так как их области определения не совпадают. Уравнения Корень (2х - 1) 2 = х (3) и 2 х - 1 = х2 (4) не равносильны, хотя их области определения и совпадают, так как уравнение (3) имеет один корень (х = 1), а уравнение (4) - два корня (х = 1 ; х = 1).

При решении любого уравнения (неравенства) его заменяют более простым равносильным уравнением (неравенством). В начальных классах формируется следующие два основных свойства равносильных преобразований.

1. Если к обеим частям уравнения (неравенства) прибавить (вычесть) выражение, имеющее ту же область определения, что и данное уравнение (неравенство), то получим уравнение (неравенство) равносильное данному.

Например, уравнения Зх=2х+4 и 3х- 2х=4 равносильны.

2 а. Если обе части уравнения умножить на выражение, имеющее ту же область определения, и которое не обращается в нуль на этой области определения, то получим уравнение, равносильное данному.

Например уравнения (3 х - 1) • (х2 + 1) = 5 (х2 + 1) и 3х - 1=5 равносильны, а (3 х 1)* (х + 1) = 5 (х + 1) и 3 х - 1=5 не равносильны.

2 б. Если обе части неравенства умножить на выражение, имеющее ту же область определения и большее нуля на этой области определения, то получим неравенство, равносильное данному.

Например, неравенства (3 х - 1) • (х2 I) > (5 х2 1) и (3 х - 1) > 5 равносильны.

В начальных классах формируется понятие об уравнении и неравенстве, их области определения, множестве решений, равносильных преобразованиях. Покажем на примерах, как можно построить обучение по их формированию.

Пример 1. Ученикам предлагается записать с помощью уравнения решение такой задачи. Сколько детей взяло яблоки, если в вазе лежало 10 яблок и каждый из детей взял по 2 яблока и осталось в вазе два яблока?

Ученики записывают 10 - 2 х == 2 и определяют, что вместо "х" можно подставить числа 1, 2, 3, 4, 5 (находят область определения). Подбором они убеждаются, что х == 4 является корнем уравнения.

Пример 1. Для отработки умений находить область определения и множество решений неравенства учащимся можно предложить ответить на вопрос: "Какие числа можно подставить в неравенство 8 - х < 3 вместо "х" и при каких из них неравенство превращается в верное числовое неравенство?" (Вместо "х" можно взять любое число, которое меньше 9; при х = б ; 7 ; 8 получается верное числовое неравенство).

Пример 3. Для формирования понятий о равносильных уравнениях (неравенствах) и их свойствах ученикам можно предложить следующее задание.

Найдите область определения и множество решений неравенства 8 - х < 3 (1), Пользуясь неравенством (1), не решая неравенства 8-х+ 4 < 3 + 4 (2) и (8 - х) • 2 < 3 • 2 (3), найдите их области определения и множество решений.

IX. Функция: область определения, область значений, способы заданий.

Определение. Функцией называется такая зависимость переменной у от переменной X , при которой каждому значению х соответствует единственное значение у . Значения, которые может принимать х называются областью определения функции. Значения, которые принимает у называются областью значений функции.

Если функциональное соответствие задается на числовом множестве, то мы имеем числовую функцию.

Числовую функцию, как и любую другую, можно задать аналитически, парами, таблицей, графом, графиком на координатной плоскости. Например, функция у =2х-1 задана аналитически.

В начальных классах функция чаще всего задается словесно (в виде текста задачи) таблицей, выражением, парами.

В начальных классах учитель должен формировать у учащихся понятие об области определения функции, области значений функции, однозначности соответствия, способах задания функции.

Пример. Детям предлагается записать в виде выражения решение следующей задачи.

Сколько килограммов крупы, расфасованной в пакеты по 2 кг осталось перенести детям, если было 20 пакетов, и каждый ребенок берет один пакет?

Дети, записывая 20 - 2 X, учатся задавать функцию аналитически.

Для отработки умений находить область определения учитель предлагает найти наибольшее количество детей, которое необходимо для переноса крупы.

Для отработки умений находить область значений функции учитель предлагает ответить на вопрос задачи, если х = 1; 2; 3; ... ; 10. При этом ученики учатся задавать функцию парами и таблицей:

Для формирования понятия об однозначности функционального соответствия учитель задает вопрос: "Может ли остаться 10 кг крупы, если ее переносили трое ребят, шестеро ребят? "Аналогичная работа должна проводиться не только при решении различных задач, в том числе и задач на прямую и обратную пропорциональность, но и при изучении выражений с переменными.

Похожие работы

Педагогические условия формирования умений учебной деятельности младших школьников

Скачать

160951

1

0

... и умения, но и определенный социальный статус. Меняются интересы, ценности ребенка, весь уклад его жизни. 3. Комплекс педагогических условий формирования умений учебной деятельности младших школьников Успех педагогической деятельности в значительной мере зависит от характера сложившихся взаимоотношений между учителем и обучаемыми. Анализ и обобщение психолого-педагогических исследований по ...

Роль долговременной памяти в формировании орфографического навыка у младших школьников на уроках русского языка

Скачать

96845

9

0

... , и целенаправленная работа, связанная с отработкой орфографических навыков в процессе ежедневного повторения.ЗАКЛЮЧЕНИЕИсследование проблемы «Роль долговременной памяти в формировании орфографического навыка» убедило нас в том, что она имеет свои сложности. Эти сложности вызваны тем, что младший школьник имеет свои психологические особенности, связанные с сохранением материала в памяти и его ...

Формирование экологически воспитанной личности младшего школьника

Скачать

124754

11

0

... : Цели, принципы, задачи Содержание Методы, формы, средства Условия Результаты Цель   Основу для становления и развития ответственного отношения к природе, формирование экологически воспитанной личности младших школьников составляет содержание учебных предметов начальной школы: ознакомление с окружающим миром, естествознание, география, ОБЖ и т.д. Они ...

Формирование умственного приёма сравнения у младших школьников в процессе решения разноуровневых упражнений по математике

Скачать

113771

6

2

... , если оно вводится целенаправленно, осознанно, с учетом характера материала, сравниваемых объектов, возраста и уровня развития школьников. РАЗДЕЛ 2. ОПЫТНО-ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ ПО ФОРМИРОВАНИЮ УМСТВЕННОГО ПРИЕМА СРАВНЕНИЯ У МЛАДШИХ ШКОЛЬНИКОВ В ПРОЦЕССЕ ИЗУЧЕНИЯ МАТЕМАТИКИ 2.1. Методика по развитию и формированию сравнения у младших школьников в процессе изучения математики ...