Зменшили у кілька разів і дістали 4, треба знайти у скільки разів зменшили число 28

28 зменшили у кілька разів і дістали 4, треба знайти у скільки разів зменшили число 28.

Розглянемо методику роботи над простими сюжетними задачами, які треба розв'язати рівнянням.

Задачі на знаходження невідомого доданка. Задача. Михайлик і Сашко знайшли 10 грибів. Михайлик знайшов 6 грибів. Скільки грибів знайшов Сашко?

Вчитель читає задачу повністю. Потім за постановленими вчителем запитаннями учні повторюють умову.

Учитель. За умовою задачі Михайлик і Сашко знайшли 10 грибів, а один Михайлик - 6 грибів. Нам невідомо скільки грибів знайшов Сашко. Позначимо кількість, які знайшов Сашко буквою х. Тепер задачу можна сформулювати так: "Михайлик і Сашко разом знайшли 10 грибів. Михайлик знайшов 6, а Сашко х грибів". Після того як учні повторюють новий текс задачі, вчитель продовжує: "Якщо б Михайлик знайшов 6 грибів, а Сашко 4, як треба було б записати, скільки всього грибів зібрали діти? (Треба до 6 додати 4). Правильно. У задачі сказано, що Михайлик знайшов 6, а Сашко - х. Як записати, скільки грибів разом знайшли діти? (Дією додавання 6+х). Складемо рівняння. Чому дорівнює за умовою задачі сума 6+х? Отже, як запишемо рівняння (6+х=10). Розв'яжемо його. У подальшій роботі над задачами такий докладний розбір не проводиться, проте час від часу його можна практикувати.

Задача. Купили зошитів на 5грн. та книжку. За всю покупку заплатили 12 грн. Скільки коштує книжка?

Після вивчення умови задачі вчитель говорить, що її треба розв'язати рівнянням. Позначимо ціну книжки буквою х. Задачу можна сформулювати так: купили зошитів на 5грн. та книжку ціною х грн. За всю покупку заплатили 12грн. Скільки коштує книжка? Якщо за зошити заплатили 5 грн, а за книжку - х грн, то всього заплатили 5+х. За умовою ця сума дорівнює 12 грн. Отже, можна скласти рівняння.5 + х=12. Розв'язуємо його, відповідаємо на запитання задачі.

Задачі на знаходження невідомого зменшуваного.

Задача.

З класу вийшло 9 дівчат і в ньому залишилося ще 7 дівчат. Скільки дівчат було у класі з початку?

Нехай у класі було х дівчат. Якщо з класу вийшло 9 дівчат, то залишилось в ньому х-9 дівчат, що за умовою дорівнює 7. Складаємо і розв'язуємо рівняння: х-9=7, відповідаємо на запитання задачі.

Задачі на знаходження невідомого від'ємника.

Задача.

Рибалка впіймав 15 рибин. Декілька маленьких рибин він випустив у річку. У нього залишилося 9 рибин. Скільки риб випустив рибалка у річку?

Нехай рибалка випустив у річку х риб. Якщо рибалка впіймав 15 рибин і з них випустив у річку х риб, то в нього залишилося 15-х рибин, що за умовою дорівнює 9. Складаємо і розв'язуємо рівняння: 15-х=9.

Таким чином можна дійти висновку, що ефективність закріплення учнями процесу розв'язування задач на знаходження невідомих компонентів залежить, насамперед, від урізноманітнення роботи вчителя, творчих завдань, які він використовує на уроці, диференціації навчання, індивідуального і психічного розвитку кожного учня зокрема та методичної підготовки вчителя.

2.5 Організація формуючого експерименту та його аналіз його результативності

Основним завданням констатуючого експеримент було визначення стану використання простих задач на знаходження невідомих компонентів у початковій школі. На основі анкетування вчителів шкіл було з'ясовано, що більшість вчителів початкових класів в тій чи іншій мірі використовують прості задачі на уроках математики і в позаурочний час. Але основна маса вчителів задовольняється розв'язуванням простих задач лише тоді, коли вони подаються на окремому уроці в підручнику і роблячи це епізодично. Ми з'ясували, що вчителі мають труднощі в доборі аналогічних задач та методики їх введення.

Учителі неправильно оцінювали індивідуальну роботу учня або не оцінювали зовсім. Вчителі зазвичай не використовують їх і в першій частині уроку, і в заключній.

У ході експерименту вивчалася і діяльність учнів у роботі над простими задачами. Щоб з'ясувати це питання, ми провели серію спостережень на уроках математики. Класи нами вибирались лише ті, де вчителі використовували прості задачі більш-менш систематично. Проводились коні рольні роботи, бесіди з учнями, вивчення зошитів, позакласна робота. Проаналізувавши результати роботи у 2 класі протягом 1 семестру ми дійшли висновку, що в середньому в 2 класі більш-менш самостійно і свідомо працювали над простими задачами лише 6-7 учнів. Учитель фіксував, як кожен учень справляється із цими задачами: повністю, частково чи зовсім не справляється. Виявляється, що в більшості випадків із задачами справляється самостійно лише 2-3 учні. Це пов'язано із несистематичністю впровадження простих задач на знаходження невідомих компонентів у підручниках і з їх малою кількістю.

На основі матеріалів констатуючого експерименту значною мірою було визначено питання добору і змісту простих задач на знаходження невідомих компонентів дій додавання і віднімання, які є в підручниках математики, так і тих задач, що вчителі добирають до уроку самостійно.

Аналізуючи завдання, над якими зустрічали учні труднощі, ми зіткнулися із потребою з'ясувати питання про форми організації роботи над цією групою задач: фронтальну, індивідуальну, групову і методику їх використання.

Вивчаючи причини, через які на багатьох уроках не знайшлося часу для запланованих вчителем задач, ми дійшли до потреби дослідити особливості використання простих задач на знаходження невідомих компонентів на різних етапах уроку і в позаурочний час.

Було визначено, які види простих задач на знаходження невідомих компонента дій потребували спеціальної експериментальної роботи щодо їх опрацювання. Для цього потрібно було вияснити, які із простих задач на знаходження невідомих компонентів дій потребують більшої уваги при вивченні матеріалу.

Завдання експерименту полягає в тому, щоб перевірити і уточнити добірку простих задач на знаходження невідомих компонентів дій додавання і віднімання, методи і форми роботи над ними, визначити ефективність застосування розробленої системи і методики її використання.

Методика формуючого експерименту включала проведення нами спеціально розроблених уроків і їх фрагментів та окремих позаурочних занять; безпосереднє проведення самим дослідником спостереження за діями вчителя і учнів; анкетування та аналіз усних відповідей і письмових контрольних робіт; проведення бесід з учнями щодо розв'язання простих задач даного виду експериментальної системи. Питання методики проведення навчання за експериментальною системою були подані нами у вигляді окремих уроків чи фрагментів уроків, які проводилися у двох других класах.

З метою з'ясування мислительної діяльності учнів були впроваджені позаурочні заняття. Вони відбувалися 1 раз на тиждень за рахунок індивідуальних занять і тривали 1 урок, тобто 40 хв. Ці додаткові заняття проводилися у тиждень математики, у години цікавинок, конкурсів юних математиків і використовувались для роботи із тими типами простих задач, яких було мало вміщено у підручнику і які заслуговували більшої уваги для вивчення. Також під час цих занять учні отримували допомогу в роботі із задачами, з якими вони не могли справитися на уроці чи вдома.

Формуючий експеримент проводився в початковій школі. Ним було охоплено 28 учнів початкових класів, зокрема 2 класу с. Іванчани Тернопільської обл., та с. Залужжя Тернопільської області.

Експеримент складався з трьох етапів:

попереднього вивчення рівня знань учнів;

формуючого етапу з елементами пошуку;

вивчення результативності дослідження.

Результативність дослідження оцінювалась на основі виконання учнями індивідуального самостійного розв'язування простих задач на знаходження невідомих компонентів, частково використовувалось порівняння результатів початкового і кінцевого зрізів, а також бесід з учителями та безпосередніх спостережень.

Відповідно до цілей і етапів експерименту ми поставили перед собою насту пні задачі:

виявити в учнів наявний (початковий) рівень сформованості вмінь розв'язувати прості задачі на знаходження невідомих компонентів;

паралельно з навчанням учнів математики в об'ємі вимог учбової програми формувати і удосконалювати їх вміння розв'язувати прості задачі даного виду відповідно до індивідуальних можливостей кожного учня;

У ході проведення першого етапу була проведена контрольна робота, яка проводилась в експериментальному і контрольному класах на початку жовтня після завершення етапу повторення навчального матеріалу за минулий рік. Контрольна робота містила 2 задачі.

І варіант.

Задача 1.

В коробці було 7 червоних олівців і декілька синіх. Всього 12 олівців. Скільки синіх олівців було в коробці?

Задача 2.

Маса свіжо викопаної глини 12 кг. Коли глину висушили, її маса зменшилась до 8 кг. Скільки води містилося в 12 кг свіжо викопаної глини?

ІІ варіант.

Задача 1.

Леся засушила кленові листки. Коли вона подарувала подрузі 6 листків, у неї залишилося ще 24 листки. Скільки листків засушила Леся?

Задача 2.

На спортивному майданчику 19 дітей грали в м’яч. Коли частина дітей вийшла з гри, на майданчику залишилося 12 дітей. Скільки дітей вийшло з гри?

Результативність дослідження оцінювалася на основі порівняння результатів початкового та кінцевого зрізів, а також бесід з учителями та безпосередніх спостережень.

У ході першого етапу експерименту була проведена контрольна робота, яка проводилася і в експериментальному і контрольному класі в вересні. Внаслідок цієї контрольної роботи ми проаналізували успішність обох класів. Результати цієї контрольної роботи узагальнено в таблиці 1.1

З таблиці видно, що результати цієї контрольної роботи приблизно однакові і в контрольному, і в експериментальному класах.

Таблиця 1.1 Успішність учнів з математики на початку року в контрольному і експериментальному класах.

Успішність в балах	Кількість учнів
	Експериментальний клас	Контрольний клас
1	-	-
2	-	-
3	-	-
4	-	-
5	2	2
6	5	5
7	5	2
8	7	5
9	2	4
10	4	4
11	3	3
12	-	-

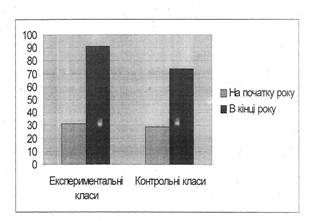
Результати контрольної роботи узагальнено в діаграмі.

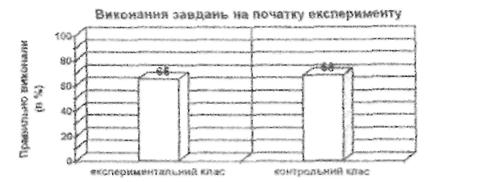
У ході формуючого експерименту було виявлено деякі труднощі, які виникали в учнів під час розв'язування цих завдань. Наприклад, при розв’язанні другої задачі деякі учнів допустили ряд помилок. Важко дітям даються задачі на знаходження невідомого від'ємника.

Труднощі, пов'язані з аналізом задачі, виявилися типовими для учнів початкових класів.

Задача

Мама дала сину 3 цукерки до обіду і декілька цукерок після обіду. Всього 11 цукерок. Скільки цукерок дала мама сину після обіду?

ілюстрацію намалювало лише декілька учнів. Коли ж вчитель разом з усім класом створив ілюстрацію, більшість учнів правильно розв'язали задачу.

З метою навчання учнів самостійно виконувати ілюстрації, ми рекомендували вчителю подавати їм на картках допомогу в вигляді рекомендацій:

Вкажи, скільки цукерок син одержав до обіду?

Скільки всього син одержав цукерок?

В цілому в експериментальних класах без додаткової підготовки із простими задачами па знаходження невідомих компонентів справилися 22-25% учнів. Основні способи подолання труднощів ми вбачали у навчанні учнів самостійно робити ілюстрації до задач у формі скороченого запису, таблиці, креслення. Зазвичай це можливо при умові, коли діти добре засвоїли відповідний вид задачі і вміють розпізнавати її. Таких труднощів в початкових класах повністю позбутися неможливо, бо вони є характерними для молодшого шкільного віку. Шляхи поступового їх подолання ми вбачаємо у регулярному проведені вчителем закріплюючого аналізу розв'язання задачі.

У ході експерименту ми прийшли до висновку, що лише сильні учні могли обходитися без допомоги вчителя, та і то не у всіх випадках. Інші ж учні класу мали труднощі і в самостійній роботі. Тому робота з ними була можлива лише у фронтальній формі. У цілому можна прийти до висновку, що у початкових класах робота над простими задачами на знаходження невідомих компонентів дій мусить бути пов'язана з елементами допомоги.

Трудність, з якою ми стикалися у ході експерименту, полягала в тому, що вчителі не завжди могли вибрати оптимальний варіант роботи із задачами. Це вимагало з нашої сторони більш точних рекомендацій учителям щодо роботи над ними та організації уроку в цілому. Ці рекомендації не були однаковими в обох класах. Трудність полягала в тому, що вчителю було важко вибрати потрібні форми і методи роботи, бо враховувати потрібно не лише співвідношення сильних, середніх і слабких учнів та загальну підготовленість класу, але і дидактичну ситуацію на уроці. Пояснимо це на прикладі роботи над простими задачами на знаходження невідомого компонента, зокрема на знаходження невідомого доданка.

Задача

На столі лежали зошити. Коли вчителька поклала ще 2, то їх стало 12. скільки зошитів лежало на столі спочатку?

Після того, як учні ознайомилися із задачею, вчителю пропонується використати задачу із використанням ілюстративного матеріалу.

Задача

Візьміть 5 синіх кружечків, покладіть до них 2 зелених.

Скільки всього кружечків? (7)

Як взнали? (5+2=7)

Якою дією? (Додавання)

Коли додаємо, стає більше чи менше, ніж було? (Більше)

При цьому розглядаємо утворення числа способом перелічування, об'єднання множин. Учні з'ясовують, що операції об'єднання множин відповідає дія додавання, а операції видалення частини множини - дія віднімання.

Тепер заберіть 2 зелених кружечки. Скільки кружечків залишилось? (5)

Як взнали? (7-2-5)

Якою дією? (Віднімання)

Коли віднімають, стає більше чи менше, ніж було? (Менше)

До першої задачі учні роблять скорочений запис, ілюструють задачу і проходить фронтальне опитування.

Було Поклали Стало

? 2 12

Інший прийом - розв'язування простих задач описуваного виду ми рекомендували для самостійної роботи для сильних і середніх учнів, при чому середні отримували допомогу. Це робилося у випадках, коли учні знайомі із розв'язуванням відповідних задач цього виду.

Задача

У магазині було 9 м'ячів. Після того, як декілька м'ячів продали, в

магазині залишилося 4 м'ячі. Скільки м'ячів продали?

Сильні учні розв'язують самостійно, а середні отримують допомогу на картці:

Треба знайти ціле чи його частину?

або

Подумай, в результаті вийде більше чи менше, ніж 9?

Окрім того, роботу над простими задачами на знаходження невідомих компонентів ми проводили не лише на уроці вивчення саме якогось виду задач, але і пропонували їх розв'язування на різних етапах інших уроків.

Так під час усного обчислення ми пропонували вчителям приділяти більшу увагу розв'язку простих задач даного виду. На етапі підведення підсумків уроку ми включали даний вид простих задач. Зокрема велику увагу приділяли їм в позаурочний час, якому було відведено 40 хв.1 раз в тиждень. Враховуючи характер виявлених помилкових міркувань, помилок і труднощів, які відчували учні під час зрізів знань на початку експерименту і під час його перебігу, ми внесли корективи в серії завдань, розробили систему підготовчих вправ, коригуючих запитань для учнів і методичних порад для вчителя. Внаслідок здійснення цих заходів склалася певна система роботи з навчання молодших школярів розв'язувати прості задачі на знаходження невідомих компонентів, яка за умови їх розвитку і мотивації в сфері навчання математики дала позитивні наслідки.

У ході експерименту порівняння ефективності навчання в експериментальних і контрольних класах здійснювалась за такими показниками:

за результатами засвоєння основного матеріалу програми з математики для початкових класів;

2) за наслідками виконання розроблених нами завдань.

3) за змінами в загальному розвитку дітей, ставленні до навчання.

В кінці II півріччя в експериментальних і контрольних класах були проведені контрольні роботи. Наведемо тексти цих робіт і результати виконання.

Задача

Оленка намалювала 8 червоних яблук і декілька жовтих. Всього вона намалювала 15 яблук. Скільки жовтих яблук намалювала дівчинка?

Задача

На дереві сиділо декілька горобців і 3 синички. Усього 10 пташок. Скільки горобців сиділо на дереві?

Задача

Мама спекла пиріжки. Коли 4 пиріжки вона віддала дітям, то в н залишилось ще 8 пиріжків. Скільки пиріжків спекла мама?

Задача

В магазин привезли 18 телевізорів. Коли декілька телевізорів магазин продав, то в ньому залишилося і це 6 телевізорів. Скільки телевізорів магазин продав?

Результати цих робіт були проаналізовані та зведені у таблиці 1.2.

Успішність в балах	Кількість учнів
	Експериментальний клас	Контрольний клас
1	-	-
2	-	-
3	-	-
4	-	-
5	1	2
6	1	4
7	3	5
8	5	3
9	6	4
10	6	4
11	5	3
12	1	-

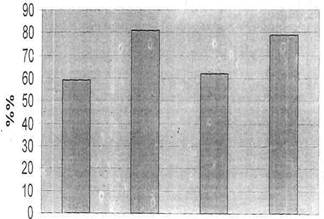
Результати виконання цих завдань узагальнені в діаграмі.

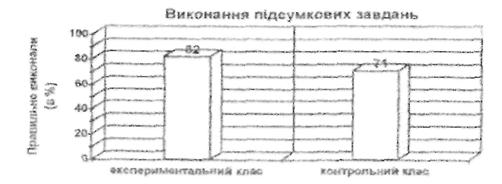
Порівнюючи успішність у експериментальному і контрольному класах, можна сказати, що у класі, де проводився експеримент, успішність учнів з математики набагато краща, ніж у контрольному класі. Ми можемо пояснити це цілеспрямованою роботою з навчання розв'язувати прості задачі даного виду, яка проводилась відповідно до завдань формуючого експерименту.

Якісне порівняння результатів розв'язання показало, що учні стали краще обґрунтовувати свої відповіді, частіше ілюструють задачу. Проте допущені помилки свідчать про необхідність додаткової роботи з учнями, побудованої на основі диференційованого підходу. Таким чином ми домоглися готовності учнів застосовувати свої знання за рахунок збільшення ініціативи середніх і слабких учнів.

Результати експерименту, оцінки вчителів свідчать про те, що запропонована нами система роботи з навчання розв'язувати прості задачі на знаходження невідомих компонентів є вагомим засобом підвищення загального рівня вивчення математики в початкових класах. Практична реалізація запропонованої системи дозволить:

підвищити загальний рівень знань учнів;

створити міцну основу для оволодіння вміннями розв'язувати прості задачі даного виду;

забезпечити умови для розвитку в учнів інтересу до математики, активізувати пізнавальну діяльність учнів

Висновки

Потреби сучасного суспільства вимагають від учнів молодшого шкільного віку повноцінного мислення, вміння розв'язувати різноманітні задачі. Одним із завдань є повноцінне використання здобутих знань на практиці. Роль задач у навчальній діяльності зростає, адже їм належить одна із провідних ролей у вивченні математики.

Проведений аналіз навчальної, методичної літератури, роботи вчителів-класоводів свідчить про те, що в теорії і практиці початкової школи проблема використання простих задач на знаходження невідомих компонентів дій додавання та віднімання має свої відображення. Проаналізувавши підручники М. Богдановича ми дійшли висновку про необхідність удосконалення методичної системи навчання молодших школярів розв'язуванню цих задач. Спираючись на концепцію розвивального навчання та на психологічні особливості дітей цього віку можна сформулювати певні вимоги до методики навчання учнів розв'язуванню цих задач:

методика повинна сприяти повній реалізації вікових пізнавальних можливостей дітей;

повинна забезпечуватись варіативність умов, у яких проходить робота вчителя і учня.

Окрім цього хочеться відмітити те, що прості задачі повинні нести відомості про навколишнє середовище, повинні бути цікавими, сприяти розвитку позитивної мотивації до процесу і результату розв'язування, повинні відповідати навчальним можливостям учнів.

Також робота із даним видом задач мас сприяти розвиваючому навчанню, оптимальному розвитку кожної дитини зокрема, забезпечувати зростання самостійності учнів, позитивно впливати на уміння розв'язувати задачі. Задачі повинні бути викладені у послідовності, певній кількості, являтися доступними та зрозумілими по змісту, бути зручними для роботи вчителя.

Нами було вивчено роботу із простими задачами на знаходження невідомих компонентів дій додавання та віднімання на різних етапах уроку. Із цього можна зробити висновок, що такі можливості є практично на всіх етапах уроку і в позаурочний час. Найкращими, на нашу думку, було опрацювання задач цих видів безпосередньо під час їх вивчення, а також при усній лічбі, у заключній частині уроку, коли є деякий час для повтору, узагальнення.

Було випробувано різні форми роботи над простими задачами на знаходження невідомого компонента дій додавання та віднімання. Зокрема, було з'ясовано, у яких випадках доцільне використання кожної із форм, описано організації усіх форм роботи на уроці, сформульовано вимоги до них, способи надання допомоги під час індивідуальної роботи.

На початку формуючого експерименту часто учні вгадували дію, якою розв’язувалась задача на знаходження невідомого зменшуваного, від'ємника. В процесі формуючого експерименту проводилася робота в результаті якої учні аналізували зв'язки між даними величинами і шуканою, і на основі цих зв’язків вибирали дію. В кінці експерименту більшість учнів вже могли обґрунтувати чому задача розв'язується власне такою дією, а не вгадували. Для цього впродовж експерименту учням пропонувалися відповідні завдання з кожного виду задач (див. додаток 2,3).

У процесі проведення експерименту вчителі отримали чіткі вказівки щодо роботи над цією групою простих задач, картки з допомогою, інструкції щодо їх використання. Окрім того, було з'ясовано, що під час посиленого опрацювання простих задач рівень знань в експериментальній групі значно покращився. Це пояснюється тим, що ми постійно закріплювали прості задачі даного виду за допомогою повторення, уподібнення. Комплексний підхід до занять з розв'язування простих задач, проведення експерименту дозволили визначити ефективність навчання.

Результати експерименту показали, що реалізація нашої системи допомагає:

підвищити загальний рівень знань з математики;

створити основу для оволодіння вміннями розв'язувані прості задачі на знаходження невідомих компонентів дій додавання та віднімання;

розвивати в учнів інтерес до математики;

активізувати пізнавальну діяльність школярів;

формувати вміння міркувати у процесі роботи над простою задачею.

Навчання учнів розв'язуванню простих задач дозволяє підвищити рівень

знань не лише сильних учнів, але і середніх і слабших.

В підсумку можемо відзначити, що поставлена мета у проведених теоретичних і експериментальних дослідженнях досягнена. Але проведене дослідження не вичерпує всіх аспектів розглянутої проблеми.

Подальшій розробці підлягають такі питання:

поглиблення вивчення диференційованого підходу до учнів;

приділення особливої уваги на засоби стимулювання математичного розвитку слабких учнів;

внесення змін у підручники з математики для початкових класів з метою більш впорядкованого вивчення цих видів простих задач.

Список використаних джерел

1.         Актуальні проблеми методики навчання математиці / Під ред. М.І. Моро, А.М. Пишкало. - М.: Педагогіка, 1977. - 248 с.

2.         Астреб А.М. Принципи систематизации арифметических задач. - К.: Рад. школа, 1939. - 56 с.

3.         Балл Г.О. У світі задач. - К.: Знання, 1986. - 44 с.

4.         Бантова М.А., Бельтюкова Г.В. Методика преподавания математики в начальних классах. - М.: Просвещение, 1984. - 335 с.

5.         Бантова М.А., Бельтюкова Г.В., Полевшикова О.М. Методика викладання математики в початкових класах. - К.: Вища школа, 1977. - 304 с.

6.         Бевз Г.П. Методика викладання математики. - К.: Вища школа, 1977. - 376с.

7.         Белюстин В.К. Методика арифметики. - М.: Типография Лисснера и Темеля, 1901. - 95 с.

8.         Богданович М.В. Математика 1. - К.: Освіта, 2001. - 128 с.

9.         Богданович М.В. Математика 2. - К.: Освіта, 2001. - 160 с.

10.      Богданович М.В. Математика 3. - К.: Освіта, 2003. - 160 с.

11.      Богданович М.В. Математика 4. - К.: Освіта, 2004. - 159 с.

12.      Богданович М.В. Диференційовані завдання з математики для 2 класу. - К.: Рад. школа, 1981. - 160 с.

13.      Богданович М.В. Методика розв'язування задач у початковій школі. - К.: Вища школа, 1990. - 182 с.

14.      Богданович М.В. Урок математики в початковій школі. - К.: Рад. школа, 1990. - 190 с.

15.      Богданович М., Козак М., Король Я. Методика викладання математики в початкових класах: Навчально-методичний посібник. - К.: А.С.К., 1998. - 352 с.

16.      Бурда М.І. Малювання сюжетних задач // 3б. статей. Розв'язування математичних задач в початкових класах. - К.: Рад. школа, 1986. - С.41-47.

17.      Вихрущ В.О. Методичні рекомендації до написання дипломних та випускних робіт. - Тернопіль, 2001. - 24 с.

18.      Вихрущ В.О. Методологія та методика наукового дослідження. - Тернопіль, 2004. - 224 с.

19.      Газдун М.І. Як учити молодших школярів розв'язувати задачі // Початкова школа. - 1988. - № 11. - С.70-72.

20.      Галубенко М. її. Як викладати математику в початковій школі. - Харків: Рад. школа, 1934. - 120 с.

21.      Давыденко И.Г. О повышении успеваимости по арифметике в начальной школе. - Харьков: Обл. метод, кабинет, 1938. - 27 с.

22.      Добржанська Л. // Початкова освіта. - 2006. - №4. - С.9.

23.      Друзь Б.Г. Творчі вправи з математики для початкових класів: Посібник для вчителів. - К.: Рад. шк., 1988. - 144с.

24.      Єрдниев П.М. Обучение математики в начальних классах. - М.: Просвещение, 1977. - 192 с.

25.      Истомина Н., Дукарт М. К вопросу об развиваюшем учебнике матиматики для начальных классов // Начальная школа. - 2000. - № 2. - С.86-90.

26.      Іванова Л.С. Робота над задачами в 1-2 класах // Початкова школа. - 1989. - №5. - С.28-32.

27.      Клименченко Д.В. Збірник вправ з математики для початкових класів. - К.: Рад. школа, 1987. - 96 с.

28.      Кодлюк Я.П. Розвивальна функція підручника для початкової школи Початкова школа. - 2002. - № 4. - С.67-71.

29.      Козак М.В., Корчевська О.П., Маланюк К.П. Уроки з математики у 2 класі чотирирічної школи. Тернопіль: Підручники і посібники, 1996. - 160 с.

30.      Колячин Ю.М. Оганесян В.А. Учись решать задачи. - М.: Просвещение, 1980. - 96 с.

31.      Контрольні роботи з математики у 2 (1) класі/М.В. Богданович, М.В. Козак, О.П. Корчевська, К.П. Маланюк. - Тернопіль: Підручники і посібники, 1995. - 32 с.

32.      Контрольні роботи з математики у 3 (2) класі/М.В. Богданович, М.В. Козак, О.П. Корчевська, К.П. Маланюк. - Тернопіль: Підручники і посібники, 1996. - 32 с.

33.      Контрольні роботи з математики у 4 (3) класі/М.В. Богданович, М.В. Козак, О.П. Корчевська, К.П. Маланюк. - Тернопіль: Підручники і посібники, 1996. - 32 с.

34.      Король Я.А., Романишин І.Я. Математика. Методика роботи над текстовими задачами 1 клас. - Тернопіль: Навчальна книга - Богдан, 2002. - 68с.

35.      Кудрявцев Л.Д. Современная математика и ее преподавание. - М.: Наука, 1985. - 176 с.

36.      Кошевская Б., Кубицель 3., Немиандерска В. К концепции исследования школьного учебника / Проблемы школьного учебника. - М.: Просвещение, 1977. - Вьіп.5. - С.164-178.

37.      Лернер И.Я. Дидактические основы методов обучения. - М.: Знание, 1976. - 64 с.

38.      Лишенко Г.П. Робота над простими задачами на знаходження невідомого компонента дії // Початкова школа. - 2003. - № 12. - С.8-9.

39.      Лишенко Г.П. Творча робота над структурою текстової задачі // Початкова школа. - 1992. - №2. - С.30-34.

40.      Мартинова Г.І. Динаміка роботи над задачею // Початкова школа. - 1986. - № 11. - С.28-32.

41.      Метельський Н.В. Дидактика математики. - Минск: Изд-во БГУ, 1982. - 256 с.

42.      Моро М.И., Бантова М.А. Математика в 2 классе. - М.: Просвещение, 1983. - 160 с.

43.      Моро М.И., Бантова М.А., Бельтюкова Г.В. Математика в 1 классе. - М: Просвещение, 1982. - 222 с.

44.      Програми для середньої загальноосвітньої школи 1-2 класи. - К.: Початкова школа, 2001. - 296 с.

45.      Програми для середньої загальноосвітньої школи 1-4 класи. - К.: Початкова школа, 2006. - 432 с.

46.      Проекти Державного освітнього стандарту з математики // Методика в школі. - 1998. - № 1. - С.4-19.

47.      Познавательные задачи в обучении гуманитарным наукам / Под ред. И.Я. Лернера. - М.: Педагогика, 1972. - 239 с.

48.      Розв'язування математичних задач у початкових класах/За ред. Т.М. Хмари. - К.: Рад. школа, 1986. - 96 с.

49.      Романишин І.Я. Математика. Методика роботи над текстовими задачами 2 клас. - Тернопіль: Навчальна книга - Богдан, 2002. - 152с.

50.      Савченко О.Я. Розвиток пізнавальної самостійності молодших школярів. - К.: Рад. школа, 1982. - 176 с.

51.      Силков В.В., Рибалко А.П. Аналіз структури задачі/Зб. статей. Розв'язування математичних задач у початкових класах. - К.: Рад. школа, 1986. - С. 19-23.

52.      Скаткин Л.Н. Обучение решению простых и составных арифметических задач. - М.: Учпедгиз, 1962. - 182 с.

53.      Тальзина Н.Ф. Управление процессом усвоения знаний. - М.: Изд-во Моск. ун-та, 1975. - 343 с.

54.      Учебный материал и учебные ситуации: Психологические аспекты/Под ред. Г.С. Костюка, Г.А. Балла. - К.: Рад. школа, 1986. - 143 с.

55.      Фридман Л.М. Логико-психологический анализ школьных учебных задач. - М: Педагогика, 1977. - 158 с.

56.      Фридман Л.М. Турецкий Е.Н., Стещенко В.Я. Как научиться решать задачи. - М: Просвешение, 1979. - 276 с.

57.      Функція і структура методів навчання/Ред.В.О. Онищука. - К.: Рад. школа, 1979. - 158 с.

58.      Ханиш Я. Теоретико-методические основьі развития творческих умений младшых школьников при обучении матиматике: Дисс. докт. пед. наук. - 13.00.02. - К., 1998. - 162 с.

59.      Царева С.Е. Прийомы первичного анализа задачи // Начальная школа. - 1985. - №9. - С.46-49.

60.      Чередов И.М. Формы учебной работы в средней школе. - М.: Просвещение, 1988. - 159 с.

61.      Шаповал І.М., Шаповал О.І. Ще одна модель розв'язування простих арифметичних задач // Початкова школа. - 1991. - № 3. - С.23-32.

Додаток 1

Творча робота над задачею. Повторне розв'язування задач.

Якщо задача повторно розв'язується відразу після запису останньої дії і відповіді, то це буде момент первинного закріплення. Мається на увазі повторне розв'язування через деякий час, через декілька днів, тижнів. Такий прийом відіграє важливу роль у формуванні і закріпленні вмінь розв'язувати задачі.

Зустрічаючись із задачею вдруге, учень краще усвідомлює зв'язки між величинами, алгоритм її розв'язання. Якщо при цьому він розв'яже її самостійно, то це вже стане його "власною" роботою над розв'язком.

Повторне розв'язування задач можна практикувати під час усної лічби, під час опитування. Один раз на місяць доцільно пропонувати учням для домашньої роботи повторно розв'язати кілька задач: одну письмово, а решту - усно.

Наприклад: за підручником всі ознайомлюються з текстом задачі. Потім один із учнів пояснює хід розв'язування. Обчислення виконувати не обов'язково, але в багатьох випадках досить пояснити зв'язки між величинами, визначити дію. Якщо ж задача важлива для подальшого вивчення, то вчитель пропонує розв'язати її, але з іншими числами всім учням класу.