Навигация
Оценка результатов учебно-познавательной деятельности младших школьников
4. Оценка результатов учебно-познавательной деятельности младших школьников.
Оценка есть определение качества достигнутых школьниками результатов обучения. На современном этапе развития начальной школы, когда приоритетной целью обучения является развитие личности школьника, определяются следующие параметры оценочной деятельности учителя:
- качество усвоения предметных знаний - умений - навыков, их соответствие требованиям государственного стандарта начального образования;
степень сформированности учебной деятельности школьника (коммуникативной, читательской, трудовой, художественной);
степень развития основных качеств умственной деятельности (умения наблюдать, анализировать, сравнивать, классифицировать, обобщать, связно излагать мысли, творчески решать учебную задачу и др.);
уровень развития познавательной активное и, интересов и отношения к учебной деятельности, степень прилежания и старания.
Первый параметр оценивается отметкой за результат обучения, остальные - словесными суждениями (характеристиками ученика). Следует обратить внимание на необходимость усиления роли постоянных наблюдений за уровнем познавательных интересов и самостоятельностью обучающегося.
Требования к оцениванию
Прежде всего, необходимо учитывать психологические особенности ребенка младшего школьного возраста: неумение объективно оценить результаты своей деятельности, слабые контроль и самоконтроль, неадекватность принятия оцени учителя и др. Любая проверка знаний должна определяться характером и объемом ранее изученного материала и уровнем общего развития учащихся.
Не менее важно требование объективности оценки. Это проявляется прежде всего в том, что оценивается результат деятельности ученика. Личное отношение учителя к школьнику не должно отражаться на оценке. Это особенно важно потому, что нередко педагог делит детей на отличников, хорошистов, троечников и, невзирая на конкретный результат работы, ставит отметку в соответствии с этим делением: отличнику оценка завышается, а троечнику - занижается.
Характер принятия школьниками оценки учителя зависит от степени сформированности у них самооценки. Реализация этого требования имеет особое значение в развитии учебно-познавательной мотивации ребенка и его отношения к учению. Отрицательной стороной деятельности учителя по контролю и оценке является его эгоцентричность.
Он стоит как бы над детьми, только сам имеет право оценить, похвалить, исправить ошибки, пожалеть, или усилить наказание. Ученик не принимает участия в этой деятельности. Более того, его участие часто наказывается («не подсказывай» - а он нашел у соседа ошибку;
«исправил» - а он у себя нашел ошибку...). Такой подход формирует у школьника убеждение в том, что оценка - проявление отношения учителя не к его деятельности, а к нему самому.
Учителю следует помнить, что одним из основных требования к оценочной деятельности является формирование у школьников умений оценивать результаты, сравнивать их с эталонными, видеть ошибки, знать требования к работам разного вида. Работа учителя состоит в создании определенного общественного мнения в классе, каким требованиям отвечает работа на «отлично», правильно ли оценена эта работа, каково общее впечатление от работы, что нужно сделать, чтобы исправить эти ошибки? Эти и другие вопросы - становятся основой коллективного обсуждения в классе и помогают развитию оценочной деятельности школьников.
Приведем пример. Учитель проводит диктант, перед сдачей предлагает его проверить. Ученик находит в своей работе ошибки и исправляет их сам. В соответствии с инструкцией учитель снижает оценку на балл. Проанализируем эту ситуацию. Ученик сам нашел ошибки, что означает наличие у него навыка самоконтроля. Естественно, в данном случае требуется не наказание, а поощрение. Но найдется учитель, который скажет: «Ученик должен сразу же писать без ошибок». Однако процесс перехода умения в навык (а именно этого требует педагог) достаточно трудный и неровный, поэтому тот факт, что умение еще не может сразу применить правило написания, скорее его беда, а не вина. И пока у школьника не сформирован тот или иной навык, он должен иметь право на исправление ошибки, на совместный с педагогом анализ причин своих неудач. Кроме того, непедагогична эта ситуация еще и потому, что у школьника формируется негативное отношение к действию самоконтроля, безразличное отношение к оцениванию («Зачем искать у себя ошибки, если учитель все равно снизит отметку?»). Противоречие, образующееся при такой ситуации, отрицательно отражается на всем учебно-воспитательном процессе, так как вносит дискомфорт в отношения между обучаемым и обучающим, между одноклассниками, детьми и родителями.
В процессе реализации воспитательной функции создаются условия для формирования тех качеств личности, которые становятся стимулом положительного отношения к учению. Это касается прежде всего умения и желания осуществлять самоконтроль. Сюда относятся: умение сравнить результат своей деятельности с эталоном; умение анализировать правильность (неправильность) выбора способа учебного действия, средств достижения цели, поиск ошибок в чужой и своей работах, анализ их причин и определение путей исправления.
Таким образом, система контроля - оценочная основа обучения становится регулятором отношений школьника и учебной среды. Ученик превращается в равноправного участника процесса обучения. Он не только готов, но стремится к проверке своих знаний, к установлению того, чего он достиг в обучении, а что ему еще предстоит преодолеть.
Учитель применяет для оценивания цифровой балл (отметку) и оценочное суждение.
Характеристика цифровой отметки и словесной оценки
Нельзя не признать, что оценивание на основе анализа текущих и итоговых отметок остаётся пока наиболее продуктивной формой. Вместе с тем следует обратить внимание на её существенные недостатки: недооценку оценочных суждений учителя, увлечение «процентоманией» субъективность выставляемых отметок.
Следует не допускать тенденции формального «накопления» отметок, ориентировку на «среднюю» отметку, выведенную путём арифметических подсчётов. Итоговая отметка не может быть простым среднеарифметическим данным по текущей проверке. Она выставляется с учётом фактического уровня подготовки, достигнутого учеником к концу определённого периода. При этом ученик получает право исправить плохую отметку, получить более высокие баллы и повысить свою успеваемость. Например, школьник получил за диктант по русскому языку «2», так как допустил грубые ошибки при применении пройденных правил орфографии. Но в последующей своей работе он усвоил эти правила и в следующем диктанте их не нарушил. Такое положение означает, что первая «2» недействительна, исправлена и не учитывается при выведении итоговой отметки.
Таким образом, следует бороться с фетишизацией отметки как единственного «орудия» формирования прилежания и мотивов учения и поощрять отказ от формализма и «процентомании». Необходимо совершенствовать, прежде всего, методику текущего контроля, усиливать значение воспитательной функции.
Ещё одной важной проблемой деятельности оценивания является разность подходов к использованию отметки в первом классе. Необходимо отказаться от выставления отметок учащимся 1-го класса в течение всего первого года. Отметка как цифровое оформление оценки вводится учителем только тогда, когда школьники знают основные характеристики разных отметок (в каком случае ставится «5», в каких случаях отметка снижается). До введения отметок не рекомендуется применять никакие другие знаки оценивания - звёздочки, цветочки, разноцветные полоски и пр. Учитель должен знать, что в данном случае функции отметки берёт на себя этот предметный знак и отношение ребёнка к нему идентично отношению к цифровой оценке.
Отметкой оценивается результат определённого этапа обучения. Пока дети только начинают познавать азы чтения, письма, счёта, пока не достигнуты сколько-нибудь определённые результаты обучения, отметка больше оценивает процесс учения, отношение ученика к выполнению конкретной учебной задачи, фиксирует неустоявшиеся умения и неосознанные знания. Исходя из этого, оценивать отметкой этот этап обучения нецелесообразно.
С учётом современных требований к оценочной деятельности в начальной школе вводится четырёхбалльная система цифровых оценок (отметок). Отменяется оценка «очень плохо» (отметка 1). Это связано с тем, что единица как отметка в начальной школе практически не используется и оценка «очень плохо» может быть приравнена к оценке «плохо». Отменяется оценка «посредственно» и вводится оценка «удовлетворительно».
Характеристика цифровой оценки (отметки):
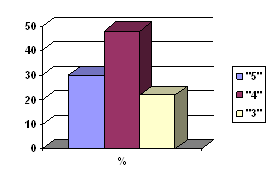
«5» («отлично») - уровень выполнения требований значительно выше удовлетворительного: отсутствие ошибок как по текущему, так и по предыдущему учебному материалу; не более одного недочёта; логичность и полнота изложения;
«4» («хорошо») - уровень выполнения требований выше удовлетворительного: использование дополнительного материала, полнота и логичность раскрытия вопроса; самостоятельность суждений, отражение своего отношения к предмету обсуждения. Наличие 2-3 ошибок или 4-6 недочётов по текущему учгГчому материалу: не более 2 ошибок или 4 ие;;''чс' "э,' пройденному материалу, незначительные нарушения логики изложения материала.
Использование нерациональных приемов решения учебной задачи; отдельные неточности в изложении материала;
«З» («удовлетворительно») - достаточный минимальный уровень выполнения требований, предъявляемых к конкретной работе; не более 4-6 ошибок или 10 недочётов по текущему учебному материалу; не более 3-5 ошибок или не более 8 недочётов по пройденному учебному материалу; отдельные нарушения логики изложения материала; неполнота раскрытия вопроса;
«2» («плохо») - уровень выполнения требований ниже удовлетворительного, наличие более 6 ошибок или 10 недочётов по текущему материалу; более 5 ошибок или более 8 недочётов по пройденному материалу; нарушение логики, неполнота, нераскрытость обсуждаемого вопроса, отсутствие аргументации либо ошибочность её основных положений.
Вводится оценка «за общее впечатление от письменной работы». Сущность ее состоит в определении отношения учителя к внешнему виду работы (аккуратность, эстетичность, привлекательность, чистота, оформленность и др.) Эта отметка ставится как дополнительная, в журнал не вносится.
Таким образом, в тетрадь (и в дневник) учитель выставляет 2 отметки (например, 5/3): за правильность выполнения учебной задачи (отметка в числителе) и за общее впечатление от работы (отметка в знаменателе). Снижение отметки «за общее впечатление от работы» допускается, если:
- в работе имеется не менее 2 неаккуратных исправлений;
- работа оформлена небрежно, плохо читаема, в тексте много зачеркиваний, клякс, неоправданных сокращений слов, отсутствуют поля и красные строки.
Данная позиция учителя в оценочной деятельности позволит более объективно оценивать результаты обучения и «развести» ответы на вопросы «чего достиг ученик в освоении предметных знаний?» и «каково его прилежание и старание?»
Характеристика словесной оценки (оценочное суждение)
Словесная оценка есть краткая характеристика результатов учебного труда школьников. Эта форма оценочного суждения позволяет раскрыть перед учеником динамику результатов его учебной деятельности, проанализировать его возможности и прилежание. Особенностью словесной оценки являются её содержательность, анализ работы школьника, чёткая фиксация (прежде всего!) успешных результатов и раскрытие причин неудач. Причём эти причины не должны касаться личностных характеристик учащегося («ленив», «невнимателен», «не старался»).
Оценочное суждение сопровождает любую отметку в качестве заключения по существу работы, раскрывающего как положительные, так и отрицательные её стороны, а также способы устранения недочётов и ошибок.
Математика Оценивание письменных работ
В основе данного оценивания лежат следующие показатели: правильность выполнения и объем выполнения задания.
Классификация ошибок и недочетов, влияющих на снижение оценки.
Ошибки:
- незнание или неправильное применение свойств, правил, алгоритмов, существующих зависимостей, лежащих в основе выполнения задания или используемых в ходе его выполнения;
- неправильный выбор действий, операций;
- неверные вычисления в случае, когда цель задания - проверка вычислительных умений и навыков;
- пропуск части математических выкладок, действий, операций, существенно влияющих на получение правильного ответа;
- несоответствие пояснительного текста, ответа задания, наименования величин выполненным действиям и полученным результатам;
несоответствие выполненных измерений и геометрических построений заданным параметрам. Недочеты:
- неправильное списывание данных (чисел, знаков, обозначений, величин);
- ошибки в записях математических терминов, символов при оформлении математических выкладок;
- неверные вычисления в случае, когда цель задания не связана с проверкой вычислительных умений и навыков;
- наличие записи действий;
- отсутствие ответа к заданию или ошибки в записи ответа.
Снижение отметки за общее впечатление от работы допускается в случаях, указанных выше.
Оценивание устных ответов
В основу оценивания устного ответа учащегося положены следующие показатели:
правильность, обоснованность, самостоятельность, полнота.
Ошибки:
- неправильный,ответ на поставленный вопрос;
- неумение ответить на поставленный вопрос или выполнение задания с помощью учителя;
- при правильном выполнении задания неумение дать соответствующие объяснения. Недочеты:
- неточный или неполный ответ на поставленный вопрос;
- при правильном ответе неумение самостоятельно или полно обосновать и проиллюстрировать его;
- неумение точно сформулировать ответ решенной задачи;
- медленный темп выполнения задания, не являющийся индивидуальной особенностью школьника;
- неправильное произношение математических терминов.
Особенности организации контроля по математике
Текущий контроль по математике можно осуществлять как в письменной, так и в устной форме. Письменные работы для текущего контроля рекомендуется проводить не реже 1 раза в неделю в форме самостоятельной работы или математического диктанта. Желательно, чтобы работы для текущего контроля состояли из нескольких однотипных заданий, с помощью которых осуществляется всесторонняя проверка только одного определенного умения (например, умения сравнивать натуральные числа, умения находить площадь прямоугольника и др.).
Тематический контроль по математике в начальной школе проводится в основном в письменной форме. Для тематических проверок выбираются узловые вопросы программы:
приемы устных вычислений, действия с многозначными числами, измерение величин и др.
Среди тематических проверочных работ особое место занимают работы, с помощью которых проверяются знания табличных случаев сложения, вычитания, умножения и деления. Для обеспечения самостоятельности учащимся подбирается несколько вариантов работы, каждый из которых содержит 30 примеров (соответственно по 15 на сложение и вычитание или умножение и деление). На выполнение такой работы отводится 5-6 минут урока.
Итоговый контроль по математике проводится в форме контрольных работ комбинированного характера (они содержат арифметические задачи, примеры, задания геометрического характера и др.). В этих работах сначала отдельно оценивается выполнение задач, примеров, заданий геометрического характера, а затем выводится итоговая отметка за всю работу.
Приложение 3
Анкета для учителей математики
1. Ф.И.О.
2. В какой школе преподаете:
3. Какими методами пользуетесь при проверке знаний, умений учащихся:
4. Пользуетесь вы или нет зачетной системой при проверке знаний, умений учащихся:
5. Как вы относитесь к урокам такого типа:
6. Что вам больше нравится в этих уроках:
7. Что вы видите положительного в уроках-зачетах:
8. Что вас не устраивает в уроках такого типа:
9. Какие новые методы проверки вам известны:
10. Как вы считаете надо ли проверять знания учащихся и для чего это нужно?
Приложение 4
Билет № 1.
1) Параллелограмм (определение). Его св-ва (сформулировать все и доказать одно свойство).
2) Квадратный трехчлен (определение). Теорема о разложении кв. трехчлена на множители.
Билет М 2.
1) Параллелограмм (определение). Его признаки (сформулировать все и доказать один признак).
2) Теорема Виета (доказательство). Теорема обратная теореме Виета (формулировка)
Билет № 3.
1) Прямоугольник (св-ва, определение, признак). Св-во диагоналей прямоугольника (Доказать)
2) Решение неполных кв. уравнений.
Билет № 4.
1) Ромб (определение, св-ва). Доказать св-ва диагоналей ромба.
2) Вывод формул корней кв. уравнения.
Билет № 5.
1) Определение прямоугольника. Теорема о площади прямоугольника.
2) Решение кв. уравнений со вторым четным коэффициентом.
Билет № 6.
1) Определение параллелограмма. Теорема о площади параллелограмма.
2) Множество действительных чисел.
Билет № 7.
1) Определение треугольника. Теорема о площади треугольника (^=1\2а На)
2) Определения кв. корня из неотрицательного числа. Св-ва кв. корня (записать все равенства). Доказательство теоремы о кв. корне из произведения.
Билет № 8.
1) Определение трапеции. Теорема о площади трапеции.
2) Определение кв. корня из неотрицательного числа. Доказательство теоремы о кв. корне из частного.
Билет № 9.
1) площадь выпуклого четырехугольника с взаимно перпендикулярными диагоналями. Площадь ромба и квадрата (Формулы)
2) Функция у=^х. Ее график, св-ва.
Билет № 10.
1) Теорема Пифагора (Доказательство). Теорема обратная теореме Пифагора (формулировка)
2) построение графиков функций у=Г(х+Ь), у=цх)+а, у=Г(х+Ь)+а, у=-цх), если известен график функций у^х).
Билет № 11.
1) зт, со5,1§, с1§ острого угла в прямоугольном треугольнике. Нахождение их значения для угла 30°.2) функция у=к\х (к>0), ее график и св-ва.
Билет № 12.
1) зт, со8,1§, с1§ острого угла в прямоугольном треугольнике. Нахождение их значения для угла 45°
2) функция у=к\х (к<0), ее график и св-ва.
Билет № 13.
1) 8т, со8, \%, с1§ острого угла в прямоугольном треугольнике. Нахождение их значения для угла 60°
2) функция у=ах (а>0), ее график и св-ва.
Билет № 14.
1) определение подобных треугольников, признак подобия треугольников (формулировка всех и доказательство одного из них).
2) функция у=ах2 (а<0), ее график и св-ва.
Билет № 15.
1) определение средней линии треугольника. Теорема о средней линии треугольника.
2) Теорема о графике функций у=ах2 + вх + с, алгоритм построения его.
Билет №16.
1) Касательная к окружности (определение, св-ва, признаки). Доказательство теоремы св-ве касательной к окружности.
2) Алгебраические дроби, основное св-во, сложение и вычитание алгебраических дробей
Билет №17.
1) Вписанный угол, теорема о вписанном угле.
2) Алгебраические дроби, умножение и деление алгебраических дробей, возведение их в степень.
Приложение 5
Срезовый тест по алгебре
1. Разложите на множители:
1. x2y2-16z2
а) (xy-yz)2 в) (xy-4z)(xy+4z)
б) (x-y-16z)2 г) (xy-16z)(xy+16z)
2. 1+6m+9m2
а) не разлагается на множители в) (3m-1)2
б) (3m+1)(3m-1) г) (3m+1)2
3. 25a2-10a+1
а) (5a-1)2 в) (5a-1)(5a+1)
б) (5a+1)2 г) не разлагается на множители
4. m3-27
а) (m-3)(m2+3m+9) в) (m-3)(m2+6m+9)
б) (m+3)(m2-3m+9) г) (m+3)(m2-6m+9)
5. 1+8b3
а) (2b-1)(4b2-2b+1) в) (1-2b)(4b2-2b+1)
б) (2b+1)(4b2-2b+1) г)(2b+1)(4b2+2b+1)
Похожие работы
... оказывают положительное воздействие на развитие памяти и мышления, воспитания воли, привычки к систематическому учебному труду и самоконтролю, повышение ответственности за выполняемую работу. Комплексное использование всех возможностей контроля и оценки успеваемости учащихся, в конечном счете, направлено на обеспечение высокого качества процесса обучения и подготовки учащихся. Теорией и ...
... заданиями, особенно, если карточка с заданием индивидуальна и ученик может работать в ней. Глава 2. Экспериментальное исследование методов и приемов систематизации и обобщения знаний учащихся при изучении темы «Алгебраические уравнения» в 9 классе 2.1. Тематическое планирование Одним из существенных моментов в организации обучения является систематизация за знаниями и умениями учащихся. ...
... одна из ее сторон – урок. В работе доказано, что самоанализ урока является основой эффективного управления процессом обучения. Дальнейшей же перспективой исследования является рассмотрение самоанализа всей деятельности учителя как основы управления процессом обучения математике. Изложенное выше позволяет считать, что самоанализ урока математики позволяет управлять процессом обучения школьников и ...
... успеваемости учащегося являются итоги (результаты) контроля. Учитываются при этом как качественные, так и количественные показатели работы учащихся. система контроль успеваемость студент 2. Применение средств контроля успеваемости студентов в ВУЗах Республики Беларусь 2.1 Использование 10-бальной системы. Сравнение 10-бальной и пятибалльной системы оценивания В Беларусь введена в 2003 ...

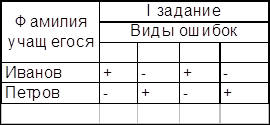
0 комментариев