Понятие марковского случайного процесса
Финальные вероятности и граф состояний СМО
Основные понятия имитационного моделирования
Граф состояний системы и уравнения Колмогорова
Расчет показатели эффективности системы по финальным вероятностям
Блок-схема программы
Статистическая обработка результатов и их сравнение с результатами аналитического моделирования
Навигация
Финальные вероятности и граф состояний СМО
Имитационное моделирование системы массового обслуживания
48014
знаков
3
таблицы
9
изображений
1.4 Финальные вероятности и граф состояний СМО
При достаточно большом времени протекания процессов в системе (при 
) могут устанавливаться вероятности состояний, не зависящие от времени, которые называются финальными вероятностями, т.е. в системе устанавливается стационарный режим. Если число состояний системы конечно, и из каждого из них за конечное число шагов м. перейти в любое другое состояние, то финальные вероятности существуют, т.е. 
Смысл финальных вероятностей состоит в том, что они равны среднему относительному времени нахождения системы в данном состоянии.
Т.к. в стационарном состоянии производные по времени равны нулю, то уравнения для финальных вероятностей получаются из уравнений Колмогорова путем приравнивания нулю их правых частей.
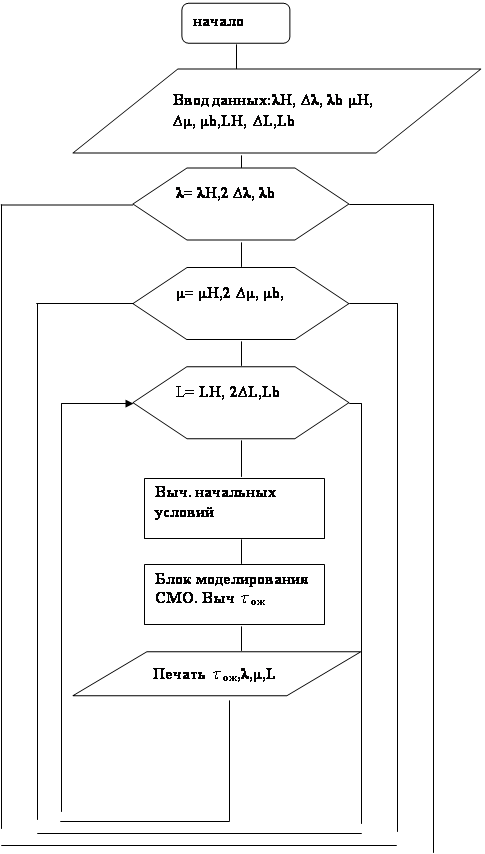
Графы состояний, используемые в моделях систем массового обслуживания, называются схемой гибели и размножения. Такое название обусловлено тем, что эта схема используется в биологических задачах, связанных с изучением численности популяции. Его особенность состоит в том, что все состояния системы можно представить в виде цепочки, в которой каждое из состояний связано с предыдущим и последующим (рис 2).
Рис. 2
Предположим, что все потоки, переводящие систему из одного состояния в другое, простейшие. По графу, представленному на рис. 2, составим уравнения для финальных вероятностей системы. Они имеют вид:
Получается система из (n+1) уравнения, которая решается методом исключения. Этот метод заключается в том, что последовательно все вероятности системы выражаются через вероятность 
.
,
,
.
Подставляя эти выражения в последнее уравнение системы, находим , затем находим остальные вероятности состояний СМО.
1.5 Показатели эффективности СМО
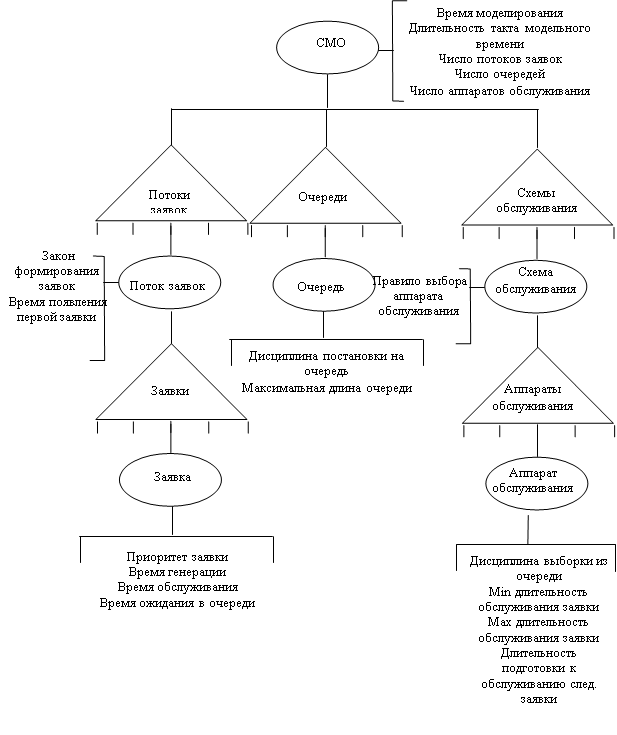
Цель моделирования СМО состоит в том, чтобы рассчитать показатели эффективности системы через ее характеристики. В качестве показателей эффективности СМО используются:
- абсолютная пропускная способность системы (А), т.е. среднее число заявок, обслуживаемых в единицу времени;
- относительная пропускная способность (Q), т.е. средняя доля поступивших заявок, обслуживаемых системой;
- вероятность отказа (
), т.е. вероятность того, что заявка покинет СМО не обслуженной;
- среднее число занятых каналов (k);
- среднее число заявок в СМО (
);
- среднее время пребывания заявки в системе (
);
- среднее число заявок в очереди (
) – длина очереди;
- среднее число заявок в системе (
);
- среднее время пребывания заявки в очереди (
);
- среднее время пребывания заявки в системе (
)
- степень загрузки канала (
), т.е. вероятность того, что канал занят;
- среднее число заявок, обслуживаемых в единицу времени;
- среднее время ожидания обслуживания;
- вероятность того, что число заявок в очереди превысит определенное значение и т.п.
Доказано, что при любом характере потока заявок, при любом распределении времени обслуживания, при любой дисциплине обслуживания, среднее время пребывания заявки в системе (очереди) равна среднему числу заявок в системе (очереди), деленному на интенсивность потока заявок, т.е.
(1.5.1)
(1.5.2)
Формулы (1.5.1) и (1.5.2) называются формулами Литтла. Они вытекают из того, что в предельном стационарном режиме среднее число заявок, прибывающих в систему, равно среднему числу заявок, покидающих ее, т.е. оба потока заявок имеют одну и ту же интенсивность 
.
Формулы для вычисления показателей эффективности приведены в таб. 1.
Таблица 1.
| Показатели | Одноканальная СМО с ограниченной очередью | Многоканальная СМО с ограниченной очередью |
| Финальные вероятности |
|
|
| Вероятность отказа |
|
|
| Абсолютная пропускная способность |
|
|
| Относительная пропускная способность |
|
|
| Среднее число заявок в очереди |
|
|
| Среднее число заявок под обслуживанием |
|
|
| Среднее число заявок в системе |
|
|
, 
Похожие работы
... очередь длины k, остается в ней с вероятностью Pk и не присоединяется к очереди с вероятностью gk=1 - Pk,'. именно так обычно ведут себя люди в очередях. В системах массового обслуживания, являющихся математическими моделями производственных процессов, возможная длина очереди ограничена постоянной величиной (емкость бункера, например). Очевидно, это частный случай общей постановки. Некоторые ...
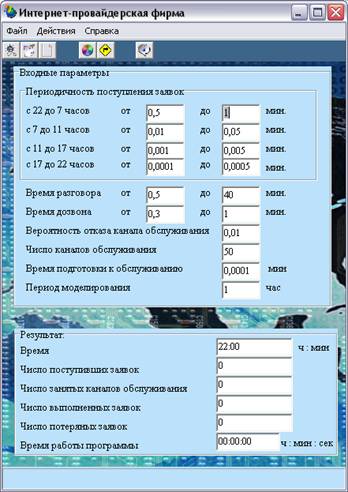
... (с 17 до 22 часов)время суток. Следовательно при одном и том же количестве каналов обслуживания, в ночное время вероятность занятости канала будет меньше, чем в дневное. Особенностью этой модели системы массового обслуживания является отсутствие очереди. Если в момент совершения заявки свободных каналов не оказалось, то она покидает систему: то есть если клиент не дозванивается, то и факт ...
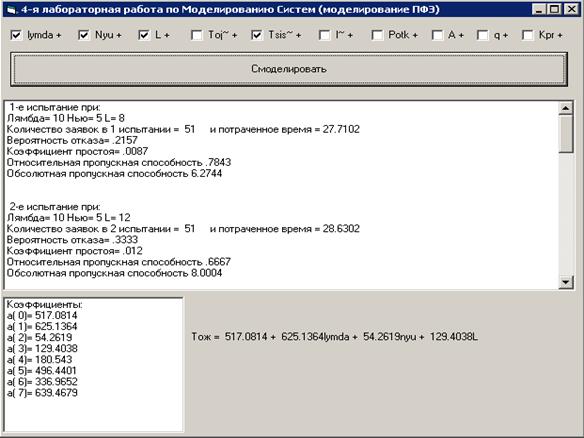
... лабораторной работе, входит: 1. Анализ зависимости влияния экзогенных переменных модели однофазной одноканальной СМО на эндогенные переменные. 2. Построение плана машинного эксперимента на основе множественного регрессионного анализа и метода наименьших квадратов. 3.Моделирование системы массового обслуживания В качестве объекта моделирования рассматривается однофазная одноканальная система, ...
... каналов обслуживан6ия, производительностью отдельного канала и эффективным обслуживанием с целью нахождения наилучших путей управления этими процессами. Задача теории массового обслуживания - установить зависимость результирующих показателей работы системы массового обслуживания (вероятности того, что заявка будет обслужена; математического ожидания числа обслуженных заявок и т.д.) от входных ...
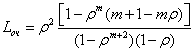
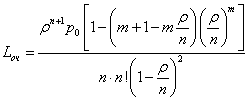
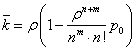
0 комментариев