Навигация
Статистическая обработка результатов и их сравнение с результатами аналитического моделирования
3.4 Статистическая обработка результатов и их сравнение с результатами аналитического моделирования
Т.к. показатели эффективности получаются в результате моделирования СМО в течение конечного времени, они содержат случайную компоненту. Поэтому, для получения более надежных результатов нужно провести их статистическую обработку. С этой целью оценим доверительный интервал для них по результатам 20 прогонов программы.
Величина ![]() попадает в доверительный интервал, если выполняется неравенство
попадает в доверительный интервал, если выполняется неравенство
 , где
, где
![]() математическое ожидание (среднее значение), находится по формуле
математическое ожидание (среднее значение), находится по формуле
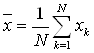 ,
,
![]() исправленная дисперсия,
исправленная дисперсия,
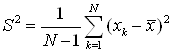 ,
,
N=20 – число прогонов,
![]() – надежность. При
– надежность. При ![]() и N=20
и N=20 ![]() .
.
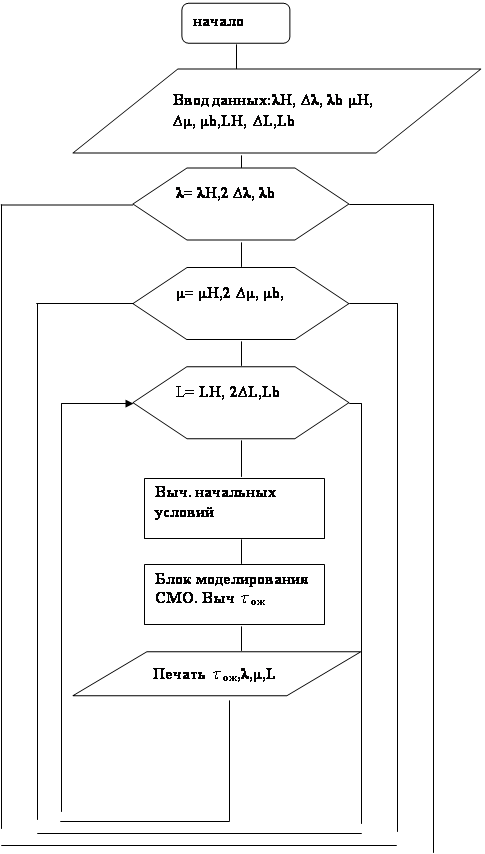
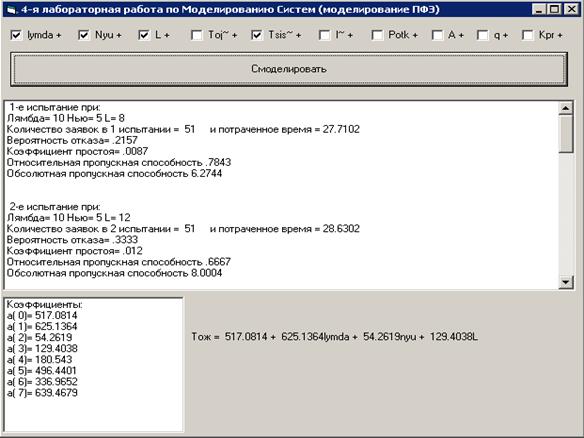
Результат работы программы представлен на рис.6.

Рис.6.
Для удобства сравнения результатов, полученных различными методами моделирования, представим их в виде таблицы.
Таблица 2.
| Показатели эффективности СМО | Результаты аналитического моделирования | Результаты имитационного моделирования | |
| Нижняя граница доверительного интервала | Верхняя граница доверительного интервала | ||
| Вероятность отказа | 0,33355 | 0,238 | 0,35979 |
| Относительная пропускная способность | 0,66645 | 0,64 | 0,761 |
| Абсолютная пропускная способность | 2.66579 | 2,56 | 3,048 |
| Средняя длина очереди | 0,917264 | 0,696 | 0,9566 |
| Среднее время пребывания заявки в очереди | 0,229316 | 0,1739 | 0,2394 |
| Среднее число занятых каналов | 2,665798 | 2,561 | 3,048 |
Из табл. 2 видно, что результаты, полученные при аналитическом моделировании СМО, попадают в доверительный интервал, полученный по результатам имитационного моделирования. Т.е., результаты, полученные разными методами, согласуются.
Заключение
В данной работе рассмотрены основные методы моделирования СМО и расчета показателей их эффективности.
Проведено моделирование четырехканальной СМО с максимальной длиной очереди равной 4 с помощью уравнений Колмогорова, а также, найдены финальные вероятности состояний системы. Рассчитаны показатели ее эффективности.
Проведено имитационное моделирование работы такой СМО. На языке программирования Delphi составлена программа, имитирующая ее работу. Проведена серия расчетов, по результатам которых найдены значения показателей эффективности системы и выполнена их статистическая обработка.
Полученные при имитационном моделировании результаты согласуются с результатами аналитического моделирования.
Литература
1. Вентцель Е.С. Исследование операций. – М.: Дрофа, 2004. – 208 с.
2. Волков И.К., Загоруйко Е.А. Исследование операций. – М.: Изд.-во МГТУ им. Н.Э. Баумана, 2002. – 435 с.
3. Волков И.К., Зуев С.М., Цветкова Г.М. Случайные процессы. – М.: Изд.-во МГТУ им. Н.Э. Баумана, 2000. – 447 с.
4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 1979. – 400 с.
5. Ивницкий В.Л. Теория сетей массового обслуживания. – М.: Физматлит, 2004. – 772 с.
6. Исследование операций в экономике/ под ред. Н.Ш. Кремера. – М.: Юнити, 2004. – 407 с.
7. Таха Х.А. Введение в исследование операций. – М.: ИД «Вильямс», 2005. – 902 с.
8. Харин Ю.С., Малюгин В.И., Кирлица В.П. и др. Основы имитационного и статистического моделирования. – Минск: Дизайн ПРО, 1997. – 288 с.
Приложение 1
Листинг программы аналитического моделирования
Программа написана в математическом пакете Maple 8.
> # Дано
la:=4:
m:=1:
Находим финальные вероятности
> usl := {m*Pf[1]-la*Pf[0] = 0,
2*m*Pf[2]-la*Pf[1] = 0,
3*m*Pf[3]-la*Pf[2] = 0,
3*m*Pf[4]-la*Pf[3] = 0,
3*m*Pf[5]-la*Pf[4] = 0,
Pf[0]+Pf[1]+Pf[2]+Pf[3]+Pf[4]+Pf[5]= 1 }:
> s:=evalf(solve(usl) ):
> for i from 0 by 1 to 5 do
Pf[i]:=subs( s, Pf[i] );
end;
![]()
![]()
![]()
![]()
![]()
![]()
>
> # Уравнения Колмогорова
> del_t:=0.01: #шаг по времени
T:=10: # Время, за которое система выходит на стационарный режим
N:=trunc(T/del_t); # Число шагов
![]()
>
> # Присваиваем начальные значения
p[i,c]:=array(0..5,0..N):
p[0,0]:=1:
for i from 1 by 1 to 5 do p[i,0]:=0 end:
> # Метод Эйлера
jj:=0:
for k from 1 to N do
v:=jj:
j:=trunc(100*v):
jj:=jj+del_t:
p[0,k] := p[0,j]+( m*p[1,j]-la*p[0,j])*del_t:
p[1,k] := p[1,j]+( la*p[0,j]+2*m*p[2,j]-p[1,j]*(m+la) )*del_t:
p[2,k] := p[2,j]+( la*p[1,j]+3*m*p[3,j]-p[2,j]*(2*m+la) )*del_t:
p[3,k] := p[3,j]+( la*p[2,j]+3*m*p[4,j]-p[3,j]*(3*m+la) )*del_t:
p[4,k] := p[4,j]+( la*p[3,j]+3*m*p[5,j]-p[4,j]*(3*m+la) )*del_t:
p[5,k] := p[5,j]+( la*p[4,j]-3*m*p[5,j] )*del_t:
end:
> for i from 0 by 1 to 5 do
P[i]=p[i,N];
end;
![]()
![]()
![]()
![]()
![]()
![]()
> # Cравним финальные вероятности с вероятностями при Т=10, водно, что они близки. R-ошибка
for i from 0 by 1 to 5 do
# Pf[i]=p[i,N]:
R[i]:=abs(Pf[i]-p[i,500]);
end;
![]()
![]()
![]()
![]()
![]()
![]()
>
> # Показатели эффективности системы
# вероятность отказа
p_otk:=Pf[5];
![]()
> # относительная пропускная способность
Q := 1-p_otk;
![]()
> # абсолютная пропускная способность
A := la*Q;
![]()
> # длина очереди
lo := Pf[4]+2*Pf[5];
![]()
> # среднее время в очереди
t0 := lo/la;
![]()
> # среднее число каналов
K := (la/m)*Q;
![]()
>
> # Вывод графиков вероятностей
cur[i]:=array(0..5):
for i from 0 by 1 to 5 do
cur[i]:=CURVES([[0,p[i,0]],[0.05,p[i,5]],[0.07,p[i,7]],[0.1,p[i,10]],[0.15,p[i,15]],
[0.2,p[i,20]],[0.3,p[i,30]],[0.4,p[i,40]],[0.5,p[i,50]],[0.75,p[i,75]],[1,p[i,100]],
[1.25,p[i,125]],[1.5,p[i,150]],[1.75,p[i,175]],[2,p[i,200]],[2.5,p[i,250]],[3,p[i,300]],
[4,p[i,400]],[5,p[i,500]] ]):
end:
> i:=0: a[i]:=PLOT(cur[i],COLOR(RGB,0,0,0)): # P0 - черный
i:=1: a[i]:=PLOT(cur[i],COLOR(RGB,0,0,1)): # P1 - синий
i:=2: a[i]:=PLOT(cur[i],COLOR(RGB,1,0,0)): # P2 - красный
i:=3: a[i]:=PLOT(cur[i],COLOR(RGB,0,1,1)): # P3 - голубой
i:=4: a[i]:=PLOT(cur[i],COLOR(RGB,1,0,1)): # P4 - малиновый
i:=5: a[i]:=PLOT(cur[i],COLOR(RGB,0,1,0)): # P5 - зеленый
> display({a[0],a[1],a[2],a[3],a[4],a[5]});
Приложение 2
Листинг программы имитационного моделирования
Программа написана на языке Delphi7.
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace CMO_misiagin
{
class CMO_work
{
Random R; // Генератор случайных чисел
public uint Max_dlina_ocheredi; // Максимальная длина очереди
public uint chislo_kanalov_in_system; // Число каналов в системе
public double Lamda; // Интенсивность потока поступления заявок
public double Mu; // Интенсивность потока обслуживания заявок
public double shag_by_time; // Шаг по времени
public double[] t_oconch_obsl_vo_vsex_canalax; // Время окончания обслуживания заявки во всех каналах
public double[] t_v_sostoijaniax_s_ocher; // Время пребывания СМО в состояниях с очередью
public double t_rab_sistem; // Время работы системы
public double summ_t_obsl_zaijvok; // Суммарное время обслуживания заявок
public uint chislo_post_zaijavok; // Число поступивших заявок
public uint chislo_otkaz_zaijavok; // Число отказанных заявок
public uint chislo_obslu_zaijavok; // Число обслуженных заявок
uint dlina_ocheredi; // Длина очереди
public uint Dlina_ocheredi
{
get
{ return dlina_ocheredi; }
set
{
if (value < 0)
{ dlina_ocheredi = 0; }
else if (value > 2)
{ }
else
{ dlina_ocheredi = value;}
}
}
// Состояния СМО {ССС,ССЗ,СЗС,ЗСС,СЗЗ,ЗСЗ,ЗЗС,ЗЗЗ,ЗЗЗ+1,ЗЗЗ+2}
enum Sostoijanija_sustem { S0, S1, S2, S3, S4, S5, S6, S7, S8, S9};
Sostoijanija_sustem tekushee_sost_sustem; // Текущее состояние системы
/// <summary>
/// Представляет модель системы массового обслуживания (СМО)
/// </summary>
/// <param name="p_chislo_kanalov_in_system">Число каналов в системе</param>
/// <param name="p_Max_dlina_ocheredi">Максимальная длина очереди</param>
/// <param name="p_Lamda">Интенсивность потока поступления завок</param>
/// <param name="p_Mu">Интенсивность потока обслуживания завок</param>
/// <param name="p_shag_by_time">Шаг по времени</param>
public CMO_work(uint p_chislo_kanalov_in_system, uint p_Max_dlina_ocheredi, double p_Lamda, double p_Mu, double p_shag_by_time)
{
SetDefaults();
R = new Random();
chislo_kanalov_in_system = p_chislo_kanalov_in_system;
Max_dlina_ocheredi = p_Max_dlina_ocheredi;
Lamda = p_Lamda;
Mu = p_Mu;
shag_by_time = p_shag_by_time;
t_oconch_obsl_vo_vsex_canalax = new double[chislo_kanalov_in_system];
t_v_sostoijaniax_s_ocher = new double[Max_dlina_ocheredi];
}
/// <summary>
/// Устанавливает значения параметров СМО по умолчанию
/// </summary>
public void SetDefaults()
{
tekushee_sost_sustem = Sostoijanija_sustem.S0;
chislo_post_zaijavok = 0;
chislo_otkaz_zaijavok = 0;
chislo_obslu_zaijavok = 0;
t_rab_sistem = 0;
summ_t_obsl_zaijvok = 0;
dlina_ocheredi = 0;
for (int i = 0; i < chislo_kanalov_in_system; i++)
{ t_oconch_obsl_vo_vsex_canalax[i] = 0; }
for (int i = 0; i < Max_dlina_ocheredi; i++)
{ t_v_sostoijaniax_s_ocher[i] = 0; }
}
/// <summary>
/// Определяет случайным образом, поступила ли заявка
/// </summary>
/// <returns>true - поступила, false = не поступила</returns>
bool prichla_li_sluchain_zaijavka()
{
double r = R.NextDouble();
if (r < (shag_by_time * Lamda))
{ return true; }
return false;
}
/// <summary>
/// Определяет случайным образом время облуживания заявки
/// </summary>
/// <returns>Время облуживания заявки</returns>
double t_obslujivania_zaijvki()
{
double r = R.NextDouble();
return (-1/Mu*Math.Log(1-r, Math.E));
}
/// <summary>
/// Определение текущего состояния
/// </summary>
/// <returns>Состояние системы</returns>
Sostoijanija_sustem opred_tec_sost()
{
Sostoijanija_sustem _sostoijanija_sustem = Sostoijanija_sustem.S0;
int k = 0;
int zanijat_chislo_kanalov_in_system = 0;
for (int i = 0; i < chislo_kanalov_in_system; i++)
{
if (t_oconch_obsl_vo_vsex_canalax[i] > 0)
{
k = 1;
zanijat_chislo_kanalov_in_system++;
}
else
{ k = 0; }
_sostoijanija_sustem += k * (i + 1);
}
if (zanijat_chislo_kanalov_in_system > 1)
{ _sostoijanija_sustem ++; }
return _sostoijanija_sustem + (int)dlina_ocheredi;
}
/// <summary>
/// Один шаг моделирования системы
/// </summary>
public void modelirovanie_sustem()
{
t_rab_sistem += shag_by_time;
tekushee_sost_sustem = opred_tec_sost();
if (dlina_ocheredi > 0)
{
t_v_sostoijaniax_s_ocher[dlina_ocheredi - 1] += shag_by_time;
for (int i = 0; i < chislo_kanalov_in_system; i++)
{
if (t_oconch_obsl_vo_vsex_canalax[i] <= 0)
{
t_oconch_obsl_vo_vsex_canalax[i] = t_obslujivania_zaijvki();
summ_t_obsl_zaijvok += t_oconch_obsl_vo_vsex_canalax[i];
dlina_ocheredi--;
break;
}
}
}
if (prichla_li_sluchain_zaijavka())
{
chislo_post_zaijavok++;
if (dlina_ocheredi < Max_dlina_ocheredi)
{
chislo_obslu_zaijavok++;
if (tekushee_sost_sustem < Sostoijanija_sustem.S7)
{
for (int i = 0; i < chislo_kanalov_in_system; i++)
{
if (t_oconch_obsl_vo_vsex_canalax[i] <= 0)
{
t_oconch_obsl_vo_vsex_canalax[i] = t_obslujivania_zaijvki();
summ_t_obsl_zaijvok += t_oconch_obsl_vo_vsex_canalax[i];
break;
}
}
}
else
{ dlina_ocheredi++; }
}
else
{ chislo_otkaz_zaijavok++; }
}
for (int i = 0; i < chislo_kanalov_in_system; i++)
{
if (t_oconch_obsl_vo_vsex_canalax[i] > 0)
{
t_oconch_obsl_vo_vsex_canalax[i] -= shag_by_time;
}
}
}
}
}
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Windows.Forms;
namespace CMO_misiagin
{
public partial class Form1 : Form
{
CMO_work work;
uint chislo_progonov;
List<double> P, Q, A, K, Lo, To, Percents_otkaz, Percents_Prin;
uint n = 3; // Число каналов
uint m = 2; // MAX длина очереди
public Form1()
{
InitializeComponent();
work = new CMO_work(n, m, (double)numericUpDown1.Value, (double)numericUpDown2.Value, (double)numericUpDown3.Value);
chislo_progonov = 0;
P = new List<double>();
Q = new List<double>();
A = new List<double>();
K = new List<double>();
Lo = new List<double>();
To = new List<double>();
Percents_otkaz = new List<double>();
Percents_Prin = new List<double>();
}
private void Form1_Load(object sender, EventArgs e)
{
button1.Enabled = false;
}
private void Rasschitat_Click(object sender, EventArgs e)
{
if (chislo_progonov>1) button1.Enabled = true;
richTextBox1.Clear();
richTextBox1.Text += " Показатели эффективности: \n";
work.SetDefaults();
work.chislo_kanalov_in_system = n;
work.Max_dlina_ocheredi = m;
work.Lamda = (double)numericUpDown1.Value;
work.Mu = (double)numericUpDown2.Value;
work.shag_by_time = (double)numericUpDown3.Value;
double Time = (double)numericUpDown4.Value;
while (work.t_rab_sistem < Time)
{
work.modelirovanie_sustem();
}
richTextBox1.Text += "Поступило заявок: \t\t\t" + work.chislo_post_zaijavok.ToString() + "\n";
richTextBox1.Text += "Очередь: \t\t\t\t" + work.Dlina_ocheredi.ToString() + "\n";
richTextBox1.Text += "Отклонено заявок: \t\t\t" + work.chislo_otkaz_zaijavok.ToString() + "\n";
// Вероятность отказа
double ver_otcaza = work.t_v_sostoijaniax_s_ocher[work.Max_dlina_ocheredi - 1] / work.t_rab_sistem;
P.Add(ver_otcaza);
richTextBox1.Text += "Вероятность отказа, Ротк: \t\t\t" + ver_otcaza.ToString() + "\n";
// Относительная пропускная способность
double otnos_prop_spos = 1 - ver_otcaza;
Q.Add(otnos_prop_spos);
richTextBox1.Text += "Относительная пропускная способность, Q: \t" + otnos_prop_spos.ToString() + "\n";
// Абсолютная пропускная способность
double absol_prop_spos = work.Lamda * otnos_prop_spos;
A.Add(absol_prop_spos);
richTextBox1.Text += "Абсолютная пропускная способность, A: \t" + absol_prop_spos.ToString() +"\n";
// Длина очереди
double dlina_ocheredi = 0;
for (int i = 0; i < work.Max_dlina_ocheredi; i++)
{
dlina_ocheredi += (i + 1) * (work.t_v_sostoijaniax_s_ocher[i] / work.t_rab_sistem);
}
Lo.Add(dlina_ocheredi);
richTextBox1.Text += "Ср длина очереди, L\x03BF: \t\t\t" + dlina_ocheredi.ToString() + "\n";
// Ср время пребывания заявки в очереди
double sr_t_preb_v_ocheredi = dlina_ocheredi / work.Lamda;
To.Add(sr_t_preb_v_ocheredi);
richTextBox1.Text += "Ср время преб-ия з. в очереди, T\x03BF, c: \t" + sr_t_preb_v_ocheredi.ToString()+"\n";
// Ср число занятых каналов
double sr_chislo_zan_can_k = absol_prop_spos / work.Mu;
K.Add(sr_chislo_zan_can_k);
richTextBox1.Text += "Ср число занятых каналов, k: \t\t" + sr_chislo_zan_can_k.ToString() + "\n";
// % отказанных заявок
double curPercents_otkaz = ((double)work.chislo_otkaz_zaijavok / (double)work.chislo_post_zaijavok) * 100d;
Percents_otkaz.Add(curPercents_otkaz);
richTextBox1.Text += "% отказанных заявок: \t\t\t" + curPercents_otkaz.ToString() + "\n";
// % обслуженных заявок
double absol_prop_sposcceptedPercents = ((double)work.chislo_obslu_zaijavok / (double)work.chislo_post_zaijavok) * 100d;
Percents_Prin.Add(absol_prop_sposcceptedPercents);
richTextBox1.Text += "% обслуженных заявок: \t\t\t" + absol_prop_sposcceptedPercents.ToString() + "\n";
// Число прогонов
chislo_progonov++;
vivod_chisla_pasch.Text = chislo_progonov.ToString();
/* if (chislo_progonov > 1)
{ RasStatistici_Click(); }*/
}
// 222222222222222 доверительные интервалы 222222222222222222222222222222222222222222222222
private void button1_Click(object sender, EventArgs e)
{
richTextBox1.Text += "\n Доверительные интервалы: \n";
double sredn_Potk = 0, sredn_Q = 0, sredn_A = 0, sredn_Lo = 0, sredn_do = 0, sredn_K = 0,
sredn_Percents_otkaz = 0, sredn_Percents_Prin = 0;
double sum_Potk = 0, sum_Q = 0, sum_A = 0, sum_Lo = 0, sum_do = 0, sum_K = 0,
sum_Percents_otkaz = 0, sum_Percents_Prin = 0;
double Potk_ot = 0, Potk_do = 0, Q_ot = 0, Q_do = 0, A_ot = 0, A_do = 0,
Lo_ot = 0, Lo_do = 0, To_ot = 0, To_do = 0, K_ot = 0, K_do = 0,
Percents_otkaz_ot = 0, Percents_otkaz_do = 0,
Percents_Prin_ot = 0, Percents_Prin_do = 0;
for (int i = 0; i < chislo_progonov; i++)
{
sredn_Potk += P[i];
sredn_Q += Q[i];
sredn_A += A[i];
sredn_Lo += Lo[i];
sredn_do += To[i];
sredn_K += K[i];
sredn_Percents_otkaz += Percents_otkaz[i];
sredn_Percents_Prin += Percents_Prin[i];
}
// Математические ожидания величин
sredn_Potk /= chislo_progonov;
sredn_Q /= chislo_progonov;
sredn_A /= chislo_progonov;
sredn_Lo /= chislo_progonov;
sredn_do /= chislo_progonov;
sredn_K /= chislo_progonov;
sredn_Percents_otkaz /= chislo_progonov;
sredn_Percents_Prin /= chislo_progonov;
// Вычисление доверительных интервалов
for (int i = 0; i < chislo_progonov; i++)
{
sum_Potk += Math.Pow((P[i] - sredn_Potk), 2);
sum_Q += Math.Pow((Q[i] - sredn_Q), 2);
sum_A += Math.Pow((A[i] - sredn_A), 2);
sum_Lo += Math.Pow((sredn_Lo - Lo[i]), 2);
sum_do += Math.Pow((sredn_do - To[i]), 2);
sum_K += Math.Pow((K[i] - sredn_K), 2);
sum_Percents_otkaz += Math.Pow((Percents_otkaz[i] - sredn_Percents_otkaz), 2);
sum_Percents_Prin += Math.Pow((Percents_Prin[i] - sredn_Percents_Prin), 2);
}
Potk_ot = sredn_Potk - (2.093d) * (Math.Sqrt((sum_Potk / (chislo_progonov - 1)) / chislo_progonov));
Potk_do = sredn_Potk + (2.093d) * (Math.Sqrt((sum_Potk / (chislo_progonov - 1)) / chislo_progonov));
Q_ot = sredn_Q - (2.093d) * (Math.Sqrt((sum_Q / (chislo_progonov - 1)) / chislo_progonov));
Q_do = sredn_Q + (2.093d) * (Math.Sqrt((sum_Q / (chislo_progonov - 1)) / chislo_progonov));
A_ot = sredn_A - (2.093d) * (Math.Sqrt((sum_A / (chislo_progonov - 1)) / chislo_progonov));
A_do = sredn_A + (2.093d) * (Math.Sqrt((sum_A / (chislo_progonov - 1)) / chislo_progonov));
Lo_ot = sredn_Lo - (2.093d) * (Math.Sqrt((sum_Lo / (chislo_progonov - 1)) / chislo_progonov));
Lo_do = sredn_Lo + (2.093d) * (Math.Sqrt((sum_Lo / (chislo_progonov - 1)) / chislo_progonov));
To_ot = sredn_do - (2.093d) * (Math.Sqrt((sum_do / (chislo_progonov - 1)) / chislo_progonov));
To_do = sredn_do + (2.093d) * (Math.Sqrt((sum_do / (chislo_progonov - 1)) / chislo_progonov));
K_ot = sredn_K - (2.093d) * (Math.Sqrt((sum_K / (chislo_progonov - 1)) / chislo_progonov));
K_do = sredn_K + (2.093d) * (Math.Sqrt((sum_K / (chislo_progonov - 1)) / chislo_progonov));
Percents_otkaz_ot = sredn_Percents_otkaz - (2.093d) * (Math.Sqrt((sum_Percents_otkaz / (chislo_progonov - 1)) / chislo_progonov));
Percents_otkaz_do = sredn_Percents_otkaz + (2.093d) * (Math.Sqrt((sum_Percents_otkaz / (chislo_progonov - 1)) / chislo_progonov));
Percents_Prin_ot = sredn_Percents_Prin - (2.093d) * (Math.Sqrt((sum_Percents_Prin / (chislo_progonov - 1)) / chislo_progonov));
Percents_Prin_do = sredn_Percents_Prin + (2.093d) * (Math.Sqrt((sum_Percents_Prin / (chislo_progonov - 1)) / chislo_progonov));
richTextBox1.Text += "Вероятность отказа, Ротк: \t\nот\t" + Potk_ot.ToString() + "\nдо\t" + Potk_do.ToString() + "\n";
richTextBox1.Text += "Относительная пропускная способность, Q: \nот\t" + Q_ot.ToString() + "\nдо\t" + Q_do.ToString() + "\n";
richTextBox1.Text += "Абсолютная пропускная способность, A: \nот\t" + A_ot.ToString() + "\nдо\t" + A_do.ToString() + "\n";
richTextBox1.Text += "Ср длина очереди, L\x03BF: \t\nот\t" + Lo_ot.ToString() + "\nдо\t" + Lo_do.ToString() + "\n";
richTextBox1.Text += "Ср время преб-ия з. в очереди, T\x03BF, c: \nот\t" + To_ot.ToString() + "\nдо\t" + To_do.ToString() + "\n";
richTextBox1.Text += "Ср число занятых каналов, k: \nот\t" + K_ot.ToString() + "\nдо\t" + K_do.ToString() + "\n";
richTextBox1.Text += "% отказанных заявок: \t\nот\t" + Percents_otkaz_ot.ToString() + "\nдо\t" + Percents_otkaz_do.ToString() + "\n";
richTextBox1.Text += "% обслуженных заявок: \t\nот\t" + Percents_Prin_ot.ToString() + "\nдо\t" + Percents_Prin_do.ToString() + "\n";
button1.Enabled = false;
}
}
}
Похожие работы
... очередь длины k, остается в ней с вероятностью Pk и не присоединяется к очереди с вероятностью gk=1 - Pk,'. именно так обычно ведут себя люди в очередях. В системах массового обслуживания, являющихся математическими моделями производственных процессов, возможная длина очереди ограничена постоянной величиной (емкость бункера, например). Очевидно, это частный случай общей постановки. Некоторые ...
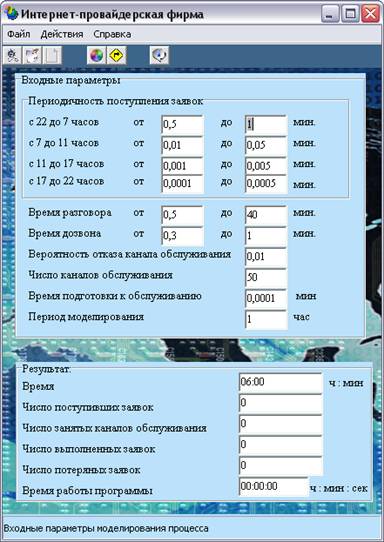
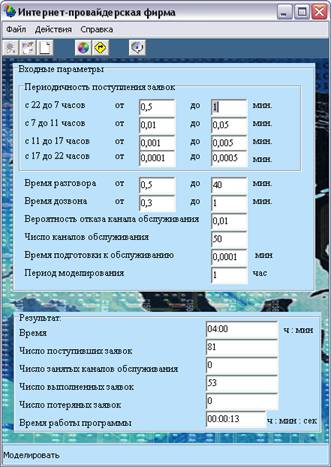
... (с 17 до 22 часов)время суток. Следовательно при одном и том же количестве каналов обслуживания, в ночное время вероятность занятости канала будет меньше, чем в дневное. Особенностью этой модели системы массового обслуживания является отсутствие очереди. Если в момент совершения заявки свободных каналов не оказалось, то она покидает систему: то есть если клиент не дозванивается, то и факт ...
... лабораторной работе, входит: 1. Анализ зависимости влияния экзогенных переменных модели однофазной одноканальной СМО на эндогенные переменные. 2. Построение плана машинного эксперимента на основе множественного регрессионного анализа и метода наименьших квадратов. 3.Моделирование системы массового обслуживания В качестве объекта моделирования рассматривается однофазная одноканальная система, ...
... каналов обслуживан6ия, производительностью отдельного канала и эффективным обслуживанием с целью нахождения наилучших путей управления этими процессами. Задача теории массового обслуживания - установить зависимость результирующих показателей работы системы массового обслуживания (вероятности того, что заявка будет обслужена; математического ожидания числа обслуженных заявок и т.д.) от входных ...


0 комментариев