Понятие марковского случайного процесса
Финальные вероятности и граф состояний СМО
Основные понятия имитационного моделирования
Граф состояний системы и уравнения Колмогорова
Расчет показатели эффективности системы по финальным вероятностям
Блок-схема программы
Статистическая обработка результатов и их сравнение с результатами аналитического моделирования
Навигация
Блок-схема программы
Имитационное моделирование системы массового обслуживания
48014
знаков
3
таблицы
9
изображений
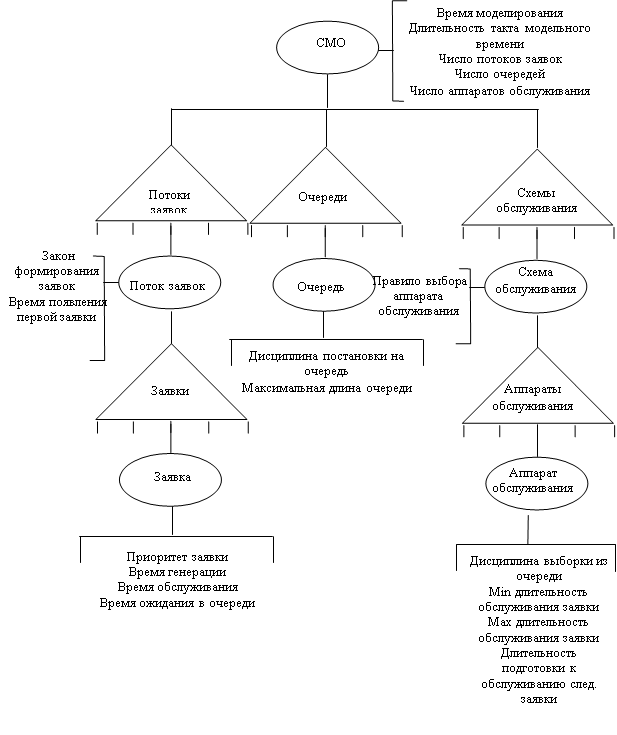
3.2 Блок-схема программы
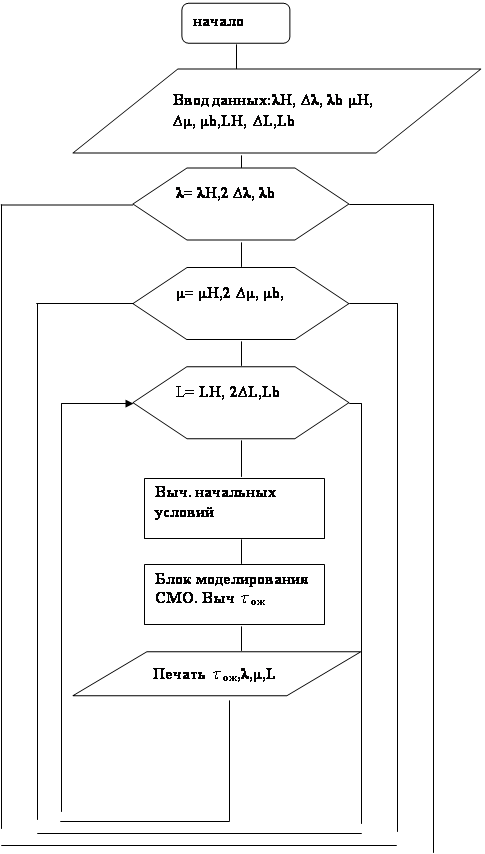
Блок-схема программы, реализующей описанный алгоритм, приведена на рис.5. Распишем некоторые блоки более подробно.
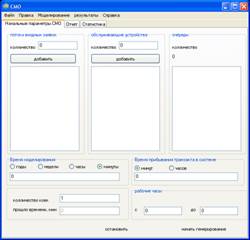
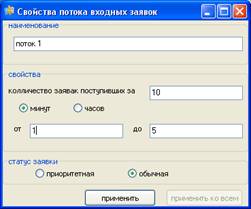
Блок 1. Задание начальных значений параметров. Пользователем задаются значения: Time – время работы системы,
r_la – интенсивность потока поступления заявок (
),
r_mu – интенсивность потока обслуживания заявок (
).
Значения, задаваемые программой:
i_deltaT:=0.001 – шаг по времени;
i_post:=0;
i_otk:= 0;
i_obsl:=0;
i_och:=0;
i_tobs:=0;
t:=0 – параметр, следящий, сколько времени проработала система;
i_obsl:=0 – число обслуженных заявок;
i_tobs:=0 – общее время обслуживания заявок в системе;
i_post:=0 – число поступивших в СМО заявок;
i_otk:=0 – число заявок, которым было отказано в обслуживании;
i_obsl:=0 – число обслуженных заявок;
sost:='s1' – состояние системы (изначально устанавливаем СМО в состояние s1, т.е. все каналы свободны);
for i :=1 to 3 do
begin
t_och[i] := 0;- обнуляем время пребывания СМО в состояниях с длиной очереди 1, 2.
t_okonch[i] := 0; – время окончания обслуживания заявки во всех 3 каналах устанавливаем в 0, т.к. каналы пусты;
end;
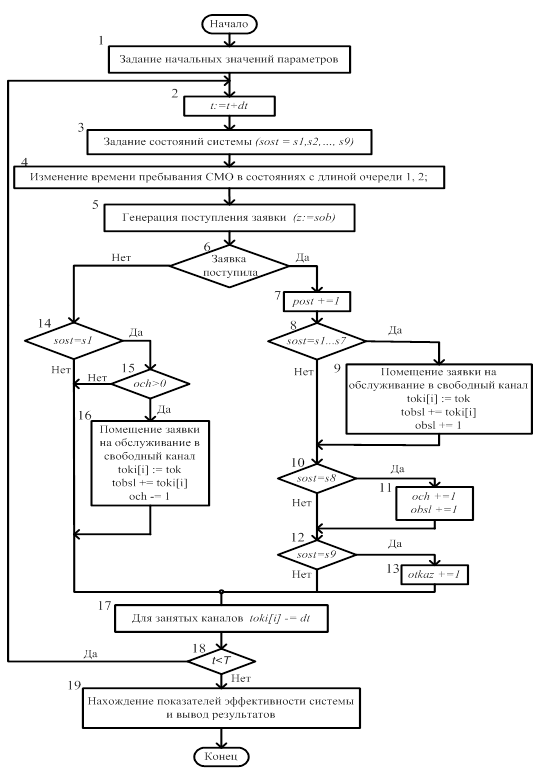
Рис.5.
Блок 3. Задание состояний системы. Выделим у данной 3-х канальной системы 9 различных состояний: s1, s2,.. s9. СМО находится в состоянии s1, когда система свободна; s2..s7 – хотя бы один канал свободен; в состоянии s8, когда все каналы заняты, и есть место в очереди; в состоянии s9 - все каналы заняты, и очередь достигла максимальной длины (och=2).
Задаем состояния системы:
_sost:=1;
for i:=0 to 3 do
begin
if t_okonch[i+1]>0 then i_temp:= 1
else i_temp:= 0;
_sost:=_sost + i_temp* round(Exp(i*ln(2)));
end;
if _sost<7 then begin Sost:= _sost; exit; end;
if (_sost= 7) and (i_och< 2) then Sost:= _sost
else
Sost := _sost+ 1;
Блок 4. Изменение времени пребывания СМО в состояниях с длиной очереди 1, 2. Это реализуется следующим программным кодом:
if i_och > 0 then t_och[i_och]:= t_och[i_och]+i_deltaT;
В блоках 9 и 16 присутствует такая операция, как помещение заявки на обслуживание в свободный канал. Просматриваются, начиная с первого, все каналы, когда выполняется условие 
(канал свободен), в него подается заявка, т.е. генерируется время окончания обслуживания заявки.
for i:=1 to 2 do
begin
if t_okonch[i]>0 then t_okonch[i]:= t_okonch[i] - i_deltaT
else
if i_och >0 then
begin
Dec(i_och);
t_okonch[i]:=tok;
i_tobs:=i_tobs + t_okonch[i];
end;
end;
Блок 17 реализуется следующим программным кодом:
for i:=1 to 2 do
if t_okonch[i]>0 then
t_okonch[i]:= t_okonch[i] - i_deltaT;
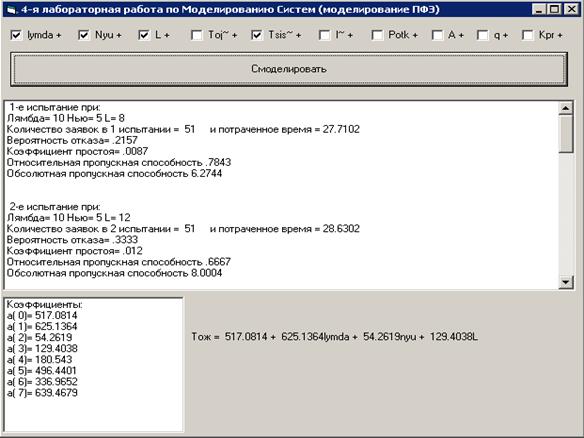
Алгоритм метода имитационного моделирования реализован на языке программирования C#.
3.3 Расчет показателей эффективности СМО на основе результатов ее имитационного моделирования
Наиболее важными являются такие показатели, как:
1) Вероятность отказа в обслуживании заявки, т.е. вероятность того, что заявка покидает систему не обслуженной. В нашем случае заявке отказывается в обслуживании, если все 3 канала заняты, и очередь максимально заполнена (т.е. 2 человека в очереди). Для нахождения вероятности отказа разделим время пребывания СМО в состоянии с очередью 4 на общее время работы системы.
2) Относительная пропускная способность – это средняя доля поступивших заявок, обслуживаемых системой.
3) Абсолютная пропускная способность – это среднее число заявок, обслуживаемых в единицу времени.
4) Длина очереди, т.е. среднее число заявок в очереди. Длина очереди равна сумме произведений числа человек в очереди на вероятность соответствующего состояния. Вероятности состояний найдем как отношение времени нахождения СМО в этом состоянии к общему времени работы системы.
5) Среднее время пребывания заявки в очереди определяется формулой Литтла
6) Среднее число занятых каналов определяется следующим образом:
7) Процент заявок, которым было отказано в обслуживании, находится по формуле
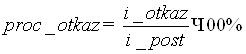
8) Процент обслуженных заявок находится по формуле
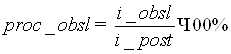
Похожие работы
... очередь длины k, остается в ней с вероятностью Pk и не присоединяется к очереди с вероятностью gk=1 - Pk,'. именно так обычно ведут себя люди в очередях. В системах массового обслуживания, являющихся математическими моделями производственных процессов, возможная длина очереди ограничена постоянной величиной (емкость бункера, например). Очевидно, это частный случай общей постановки. Некоторые ...
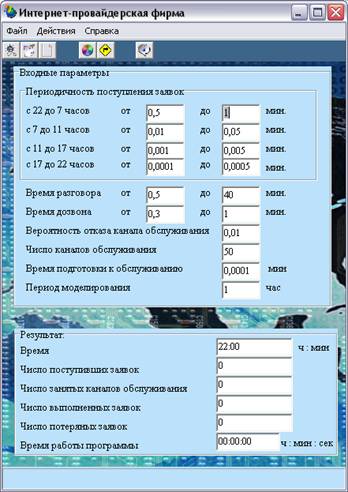
... (с 17 до 22 часов)время суток. Следовательно при одном и том же количестве каналов обслуживания, в ночное время вероятность занятости канала будет меньше, чем в дневное. Особенностью этой модели системы массового обслуживания является отсутствие очереди. Если в момент совершения заявки свободных каналов не оказалось, то она покидает систему: то есть если клиент не дозванивается, то и факт ...
... лабораторной работе, входит: 1. Анализ зависимости влияния экзогенных переменных модели однофазной одноканальной СМО на эндогенные переменные. 2. Построение плана машинного эксперимента на основе множественного регрессионного анализа и метода наименьших квадратов. 3.Моделирование системы массового обслуживания В качестве объекта моделирования рассматривается однофазная одноканальная система, ...
... каналов обслуживан6ия, производительностью отдельного канала и эффективным обслуживанием с целью нахождения наилучших путей управления этими процессами. Задача теории массового обслуживания - установить зависимость результирующих показателей работы системы массового обслуживания (вероятности того, что заявка будет обслужена; математического ожидания числа обслуженных заявок и т.д.) от входных ...
0 комментариев